3.10.5 Shortest Distances with Lines

Shortest Distance Between a Point and a Line

How do I find the shortest distance from a point to a line?

The shortest distance from any point to a line will always be the perpendicular distance

Given a line l with equation $r = a + λ b$ and a point P not on l
The scalar product of the direction vector, b, and the vector in the direction of the shortest distance will be zero

The shortest distance can be found using the following steps:

STEP 1: Let the vector equation of the line be r and the point not on the line be P, then the point on the line closest to P will be the point F

The point F is sometimes called the foot of the perpendicular

STEP 2: Sketch a diagram showing the line l and the points P and F

The vector $\vec{F P}$ will be perpendicular to the line l

STEP 3: Use the equation of the line to find the position vector of the point F in terms of λ
STEP 4: Use this to find the displacement vector $\vec{F P}$ in terms of λ
STEP 5: The scalar product of the direction vector of the line l and the displacement vector $\vec{F P}$ will be zero

Form an equation $\vec{F P} \cdot b = 0$ and solve to find λ

STEP 6: Substitute λ into $\vec{F P}$ and find the magnitude $|\vec{F P}|$

The shortest distance from the point to the line will be the magnitude of $\vec{F P}$

Note that the shortest distance between the point and the line is sometimes referred to as the length of the perpendicular

7-3-4-foot-of-the-perpendicular

How do we use the vector product to find the shortest distance from a point to a line?

The vector product can be used to find the shortest distance from any point to a line on a 2-dimensional plane
Given a point, P, and a line r = a + λb

The shortest distance from P to the line will be $\frac{|\vec{A P} \times b|}{|b|}$
Where A is a point on the line
This is not given in the formula booklet

Exam Tip

Column vectors can be easier and clearer to work with when dealing with scalar products.

Worked Example

Point A has coordinates (1, 2, 0) and the line $l$ has equation $r = (\begin{matrix} 2 \\ 0 \\ 6 \end{matrix}) + λ (\begin{matrix} 0 \\ 1 \\ 2 \end{matrix})$ .

Point B lies on the $l$ such that $[A B]$ is perpendicular to $l$ .

Find the shortest distance from A to the line $l$ .

3-10-5-ib-aa-hl-short-distance-lines-we-1

Shortest Distance Between Two Lines

How do we find the shortest distance between two parallel lines?

Two parallel lines will never intersect
The shortest distance between two parallel lines will be the perpendicular distance between them
Given a line $l_{1}$ with equation $r = a_{1} + λ d_{1}$ and a line $l_{2}$ with equation $r = a_{2} + μ d_{2}$ then the shortest distance between them can be found using the following steps:

STEP 1: Find the vector between $a_{1}$ and a general coordinate from $l_{2}$ in terms of μ
STEP 2: Set the scalar product of the vector found in STEP 1 and the direction vector $d_{1}$ equal to zero

Remember the direction vectors $d_{1}$ and $d_{2}$ are scalar multiples of each other and so either can be used here

STEP 3: Form and solve an equation to find the value of μ
STEP 4: Substitute the value of μ back into the equation for $l_{2}$ to find the coordinate on $l_{2}$ closest to $l_{1}$
STEP 5: Find the distance between $a_{1}$ and the coordinate found in STEP 4

Alternatively, the formula $\frac{|\vec{A B} \times d|}{|d|}$ can be used

Where $\vec{A B}$ is the vector connecting the two given coordinates $a_{1}$ and $a_{2}$
d is the simplified vector in the direction of $d_{1}$ and $d_{2}$
This is not given in the formula booklet

How do we find the shortest distance from a given point on a line to another line?

The shortest distance from any point on a line to another line will be the perpendicular distance from the point to the line
If the angle between the two lines is known or can be found then right-angled trigonometry can be used to find the perpendicular distance

The formula $\frac{|\vec{A B} \times d|}{|d|}$ given above is derived using this method and can be used

Alternatively, the equation of the line can be used to find a general coordinate and the steps above can be followed to find the shortest distance

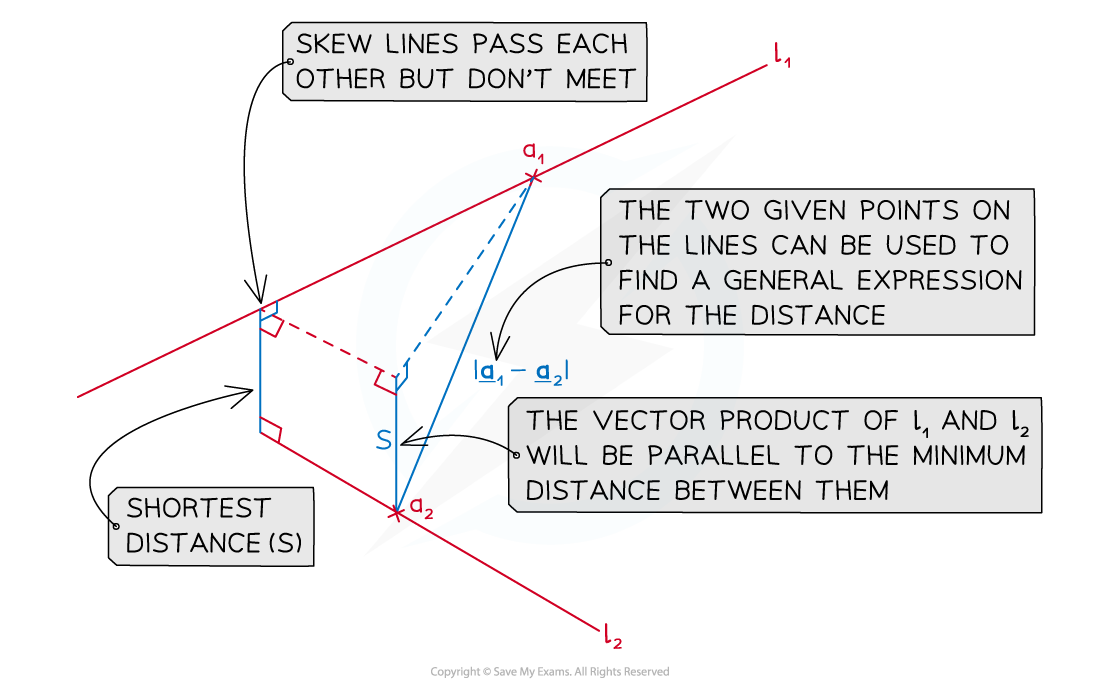
How do we find the shortest distance between two skew lines?

Two skew lines are not parallel but will never intersect
The shortest distance between two skew lines will be perpendicular to both of the lines
- This will be at the point where the two lines pass each other with the perpendicular distance where the point of intersection would be
- The vector product of the two direction vectors can be used to find a vector in the direction of the shortest distance
- The shortest distance will be a vector parallel to the vector product
To find the shortest distance between two skew lines with equations $r = a_{1} + λ d_{1}$ and $r = a_{2} + μ d_{2}$ ,
- STEP 1: Find the vector product of the direction vectors $d_{1}$ and $d_{2}$
  - $d = d_{1} \times d_{2}$
- STEP 2: Find the vector in the direction of the line between the two general points on $l_{1}$ and $l_{2}$ in terms of λ and μ
  - $\vec{A B} = b - a$
- STEP 3: Set the two vectors parallel to each other
  - $d = k \vec{A B}$
- STEP 4: Set up and solve a system of linear equations in the three unknowns, $k, λ$ and $μ$

3-10-5-ib-aa-hl-short-distance-lines-diagram-1

Exam Tip

Exam questions will often ask for the shortest, or minimum, distance within vector questions
If you’re unsure start by sketching a quick diagram
Sometimes calculus can be used, however usually vector methods are required

Worked Example

Consider the skew lines $l_{1}$ and $l_{2}$ as defined by:

$l_{1}$ : $r = (\begin{matrix} 6 \\ - 4 \\ 3 \end{matrix}) + λ (\begin{matrix} 2 \\ - 3 \\ 4 \end{matrix})$

$l_{2}$ : $r = (\begin{matrix} - 5 \\ 4 \\ - 8 \end{matrix}) + μ (\begin{matrix} - 1 \\ 2 \\ 1 \end{matrix})$

Find the minimum distance between the two lines.

3-10-5-ib-aa-hl-short-distance-lines-we-2

DP IB Maths: AA HL

Revision Notes

3.10.5 Shortest Distances with Lines

Shortest Distance Between a Point and a Line

How do I find the shortest distance from a point to a line?

How do we use the vector product to find the shortest distance from a point to a line?

Exam Tip

Worked Example

Shortest Distance Between Two Lines

How do we find the shortest distance between two parallel lines?

How do we find the shortest distance from a given point on a line to another line?

How do we find the shortest distance between two skew lines?

Exam Tip

Worked Example

Author: Amber

Resources

Members

Company

Quick Links