DP IB Maths: AA HL

Revision Notes

Home / IB / Maths: AA HL / DP / Revision Notes / 5. Calculus / 5.10 Differential Equations / 5.10.1 Numerical Solutions to Differential Equations

5.10.1 Numerical Solutions to Differential Equations

First Order Differential Equations

What is a differential equation?

A differential equation is simply an equation that contains derivatives

For example $\frac{d y}{d x} = 12 x y^{2}$ is a differential equation
And so is $\frac{d^{2} x}{d t^{2}} - 5 \frac{d x}{d t} + 7 x = 5 \sin t$

What is a first order differential equation?

A first order differential equation is a differential equation that contains first derivatives but no second (or higher) derivatives

For example $\frac{d y}{d x} = 12 x y^{2}$ is a first order differential equation
But $\frac{d^{2} x}{d t^{2}} - 5 \frac{d x}{d t} + 7 x = 5 \sin t$ is not a first order differential equation, because it contains the second derivative $\frac{d^{2} x}{d t^{2}}$

Wait – haven’t I seen first order differential equations before?

Yes you have!

For example $\frac{d y}{d x} = 3 x^{2}$ is also a first order differential equation, because it contains a first derivative and no second (or higher) derivatives
But for that equation you can just integrate to find the solution y = x³ + c (where c is a constant of integration)

In this section of the course you learn how to solve differential equations that can’t just be solved right away by integrating

Euler’s Method: First Order

What is Euler’s method?

Euler’s method is a numerical method for finding approximate solutions to differential equations
It treats the derivatives in the equation as being constant over short ‘steps’
The accuracy of the Euler’s Method approximation can be improved by making the step sizes smaller

How do I use Euler’s method with a first order differential equation?

STEP 1: Make sure your differential equation is in $\frac{d y}{d x} = f (x, y)$ form
STEP 2: Write down the recursion equations using the formulae $y_{n + 1} = y_{n} + h \times f (x_{n}, y_{n})$ and $x_{n + 1} = x_{n} + h$ from the exam formula booklet

h in those equations is the step size
the exam question will usually tell you the correct value of h to use

STEP 3: Use the recursion feature on your GDC to calculate the Euler’s method approximation over the correct number of steps

the values for $x_{0}$ and $y_{0}$ will come from the boundary conditions given in the question

Exam Tip

Be careful with letters – in the equations in the exam, and in your GDC’s recursion calculator, the variables may not be x and y
If an exam question asks you how to improve an Euler’s method approximation, the answer will almost always have to do with decreasing the step size!

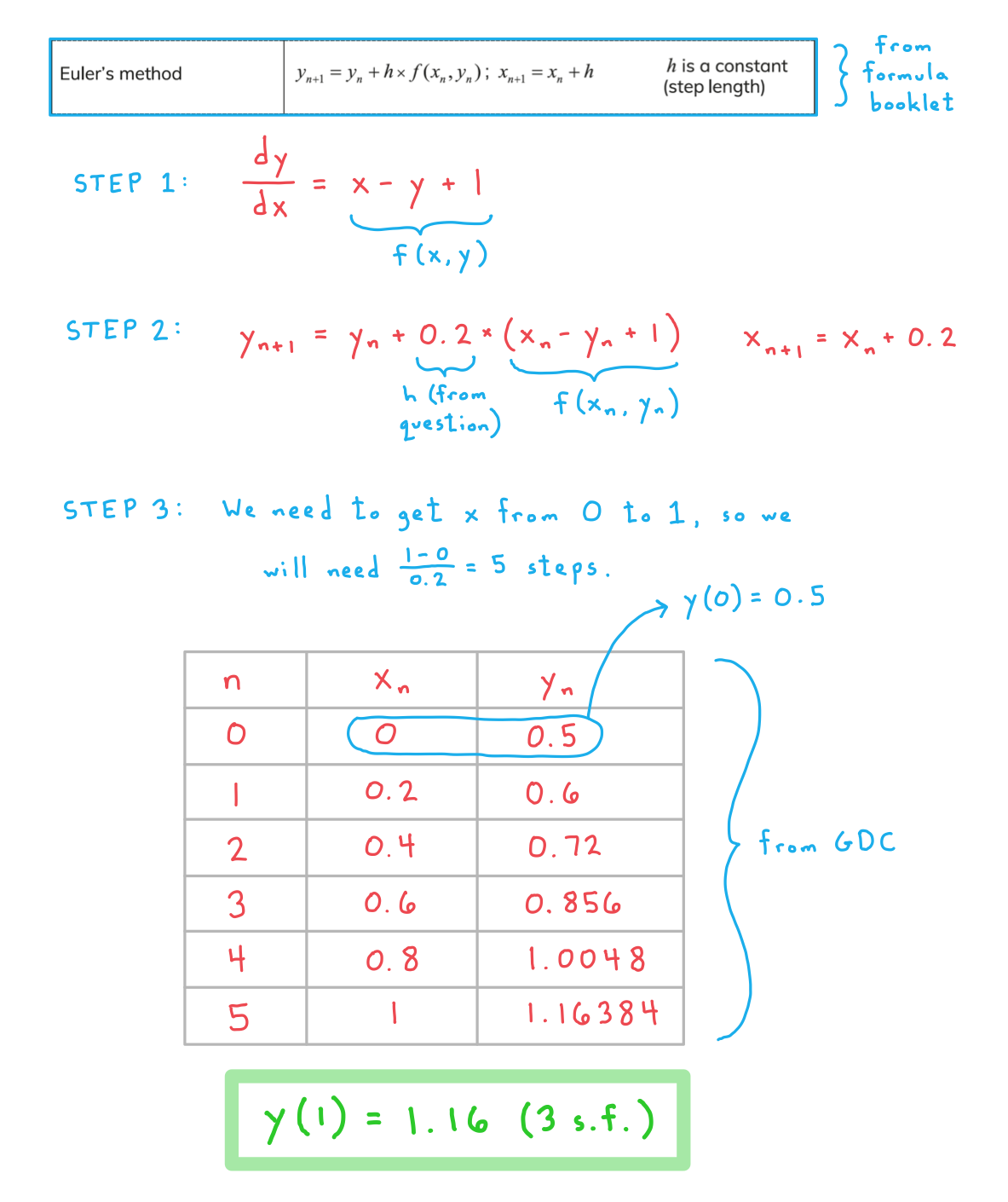
Worked Example

Consider the differential equation $\frac{d y}{d x} + y = x + 1$ with the boundary condition $y (0) = 0.5$ .

a)

Apply Euler’s method with a step size of $h = 0.2$ to approximate the solution to the differential equation at $x = 1$ .

seNtq8Uv_5-10-1-ib-aa-hl-eulers-method-a-we-solution

b)

Explain how the accuracy of the approximation in part (a) could be improved.

gY7RyKZ9_5-10-1-ib-aa-hl-eulers-method-b-we-solution

Roger Bliss

Author: Roger

Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

Resources

Home Join Support

Members

Members Home Account Logout

Company

About Us Contact Us Jobs Terms Privacy Facebook Twitter

Quick Links

GCSE Revision Notes IGCSE Revision Notes A Level Revision Notes Biology Chemistry Physics Maths 2022 Advance Information

© IB Documents (2) Team & u/aimlesskr
IBO was not involved in the production of, and does not endorse, the resources created by Save My Exams.