2.6.4 Composite Transformations of Graphs

$y = f (x + k)$ is horizontal translation by vector $(\begin{matrix} - k \\ 0 \end{matrix})$
- If k is positive then the graph moves left
- If k is negative then the graph moves right
$y = f (x) + k$ is vertical translation by vector $(\begin{matrix} 0 \\ k \end{matrix})$
- If k is positive then the graph moves up
- If k is negative then the graph moves down
$y = f (k x)$ is a horizontal stretch by scale factor $\frac{1}{k}$ centred about the y-axis
- If k > 1 then the graph gets closer to the y-axis
- If 0 < k < 1 then the graph gets further from the y-axis
$y = k f (x)$ is a vertical stretch by scale factor $k$ centred about the x-axis
- If k > 1 then the graph gets further from the x-axis
- If 0 < k < 1 then the graph gets closer to the x-axis
$y = f (- x)$ is a horizontal reflection about the y-axis
- A horizontal reflection can be viewed as a special case of a horizontal stretch
$y = - f (x)$ is a vertical reflection about the x-axis
- A vertical reflection can be viewed as a special case of a vertical stretch

Horizontal and vertical transformations are independent of each other
- The horizontal transformations involved will need to be applied in their correct order
- The vertical transformations involved will need to be applied in their correct order
Suppose there are two horizontal transformation H₁then H₂ and two vertical transformations V₁then V₂thenthey can be applied in the following orders:
- Horizontal then vertical:
  - H₁H₂V₁V₂
- Vertical then horizontal:
  - V₁V₂H₁H₂
- Mixed up (provided that H₁ comes before H₂ and V₁ comes before V2):
  - H₁V₁H₂V₂
  - H₁V₁V₂H₂
  - V₁H₁V₂H₂
  - V₁H₁H₂V₂

In an exam you are more likely to get the correct solution if you deal with one transformation at a time and sketch the graph after each transformation

The diagram below shows the graph of $y = f (x)$ .

we-image

Sketch the graph of $y = \frac{1}{2} f (\frac{x}{2})$ .

2-5-4-ib-aa-sl-comp-transformation-a-we-solution

The diagram below shows the graph of $y = f (x)$ .

we-image

Sketch the graph of $y = 3 f (x) - 2$ .

2-5-4-ib-aa-sl-comp-transformation-b-we-solution

The diagram below shows the graph of $y = f (x)$ .

we-image Sketch the graph of $y = f (2 x - 1)$ .

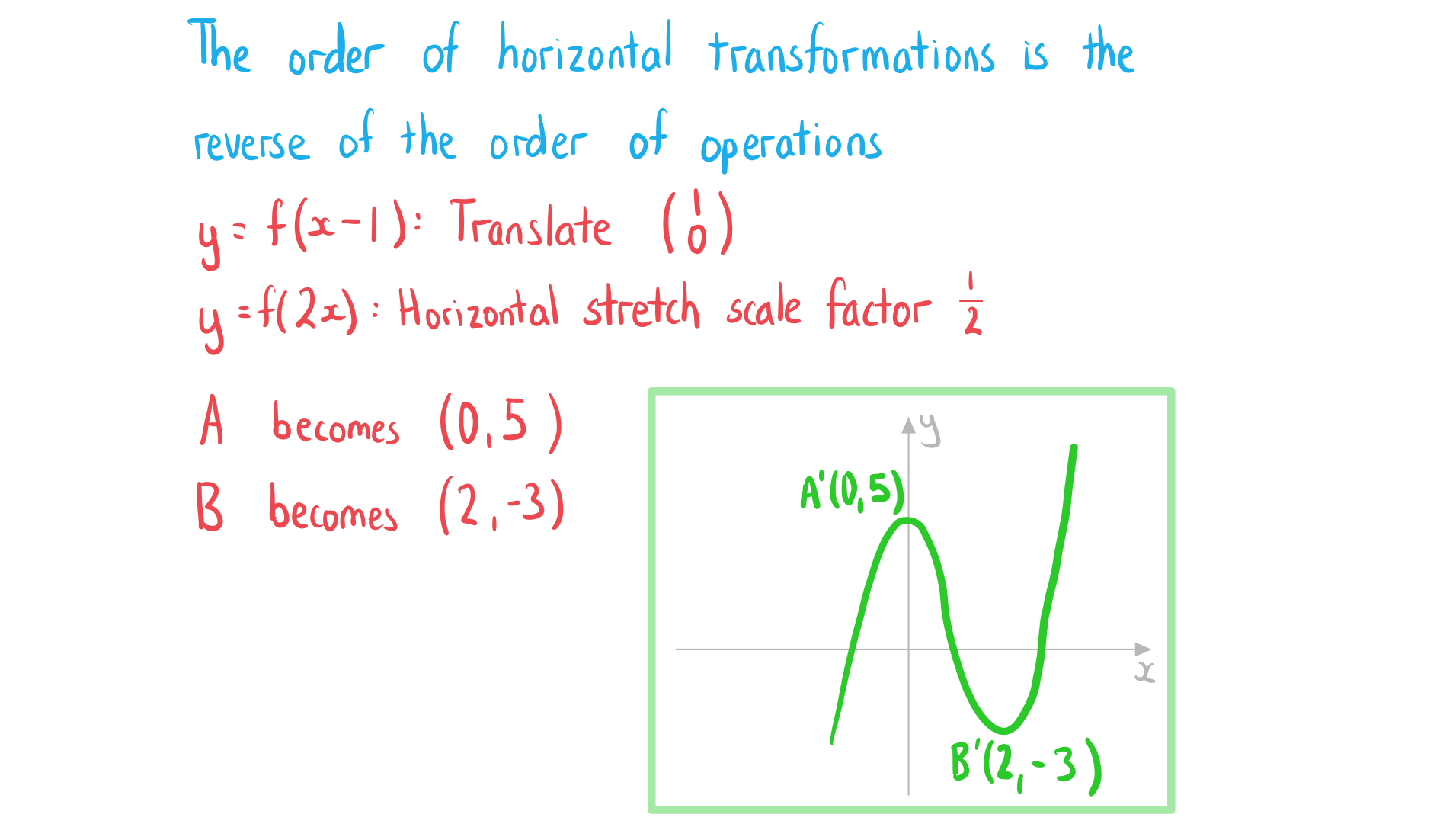
2-6-4-ib-aa--ai-hl-comp-horizontal-trans-we-solution

DP IB Maths: AA HL

2.6.4 Composite Transformations of Graphs