2.9.4 Reciprocal & Square Transformations

Reciprocal Transformations

What effects do reciprocal transformations have on the graphs?

The x-coordinates stay the same
The y-coordinates change

Their values become their reciprocals

The coordinates (x, y) become $(x, \frac{1}{y})$ where y ≠ 0

If y = 0 then a vertical asymptote goes through the original coordinate
Points that lie on the line y = 1 or the line y = -1 stay the same

How do I sketch the graph of the reciprocal of a function: y = 1/f(x)?

Sketch the reciprocal transformation by considering the different features of the original graph
Consider key points on the original graph

If (x₁, y₁) is a point on y = f(x) where y₁ ≠ 0

$(x_{1}, \frac{1}{y_{1}})$ is a point on $y = \frac{1}{f (x)}$
If |y₁|< 1 then the point gets further away from the x-axis
If |y₁|> 1 then the point gets closer to the x-axis

If y = f(x) has a y-intercept at (0, c) where c ≠ 0

The reciprocal graph $y = \frac{1}{f (x)}$ has a y-intercept at $(0, \frac{1}{c})$

If y = f(x) has a root at (a, 0)

The reciprocal graph $y = \frac{1}{f (x)}$ has a vertical asymptote at $x = a$

If y = f(x) has a vertical asymptote at $x = a$

The reciprocal graph $y = \frac{1}{f (x)}$ has a discontinuity at (a, 0)
The discontinuity will look like a root

If y = f(x) has a local maximum at (x₁, y₁) where y₁ ≠ 0

The reciprocal graph $y = \frac{1}{f (x)}$ has a local minimum at $(x_{1}, \frac{1}{y_{1}})$

If y = f(x) has a local minimum at (x₁, y₁) where y₁ ≠ 0

The reciprocal graph $y = \frac{1}{f (x)}$ has a local maximum at $(x_{1}, \frac{1}{y_{1}})$

Consider key regions on the original graph

If y = f(x) is positive then $y = \frac{1}{f (x)}$ is positive

If y = f(x) is negative then $y = \frac{1}{f (x)}$ is negative

If y = f(x) is increasing then $y = \frac{1}{f (x)}$ is decreasing

If y = f(x) is decreasing then $y = \frac{1}{f (x)}$ is increasing

If y = f(x) has a horizontal asymptote at y = k

$y = \frac{1}{f (x)}$ has a horizontal asymptote at $y = \frac{1}{k}$ if k ≠ 0
$y = \frac{1}{f (x)}$ tends to ± ∞ if k = 0

If y = f(x) tends to ± ∞ as x tends to +∞ or -∞

$y = \frac{1}{f (x)}$ has a horizontal asymptote at $y = 0$

Worked Example

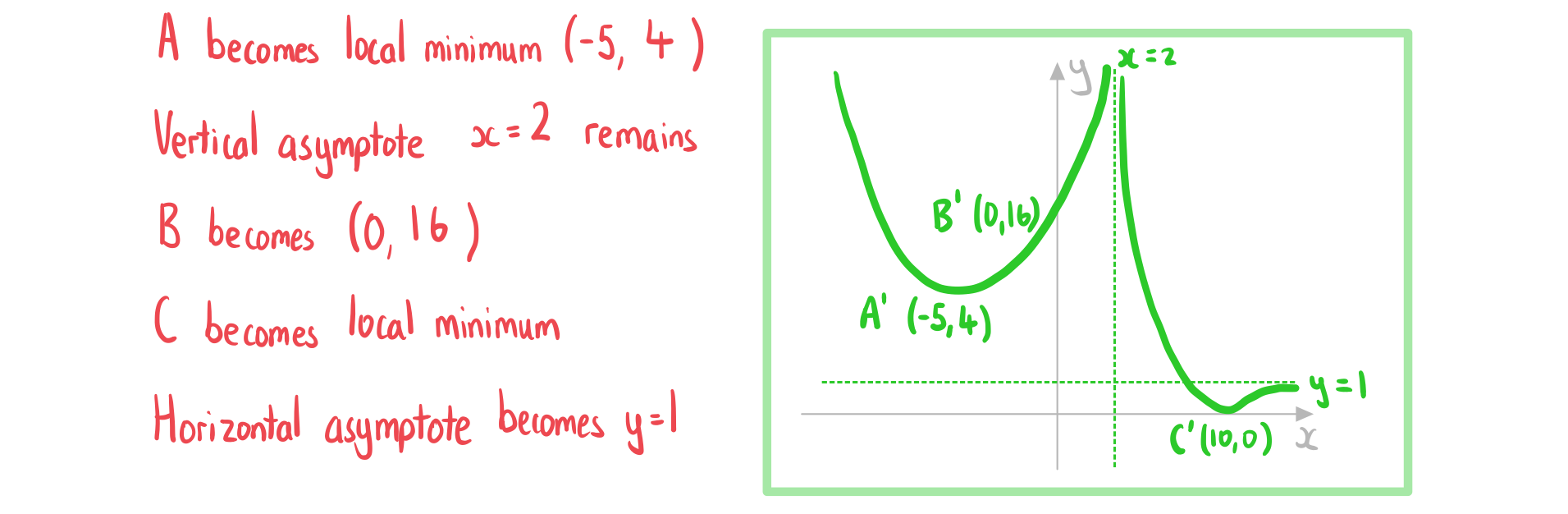
The diagram below shows the graph of $y = f (x)$ which has a local maximum at the point A.

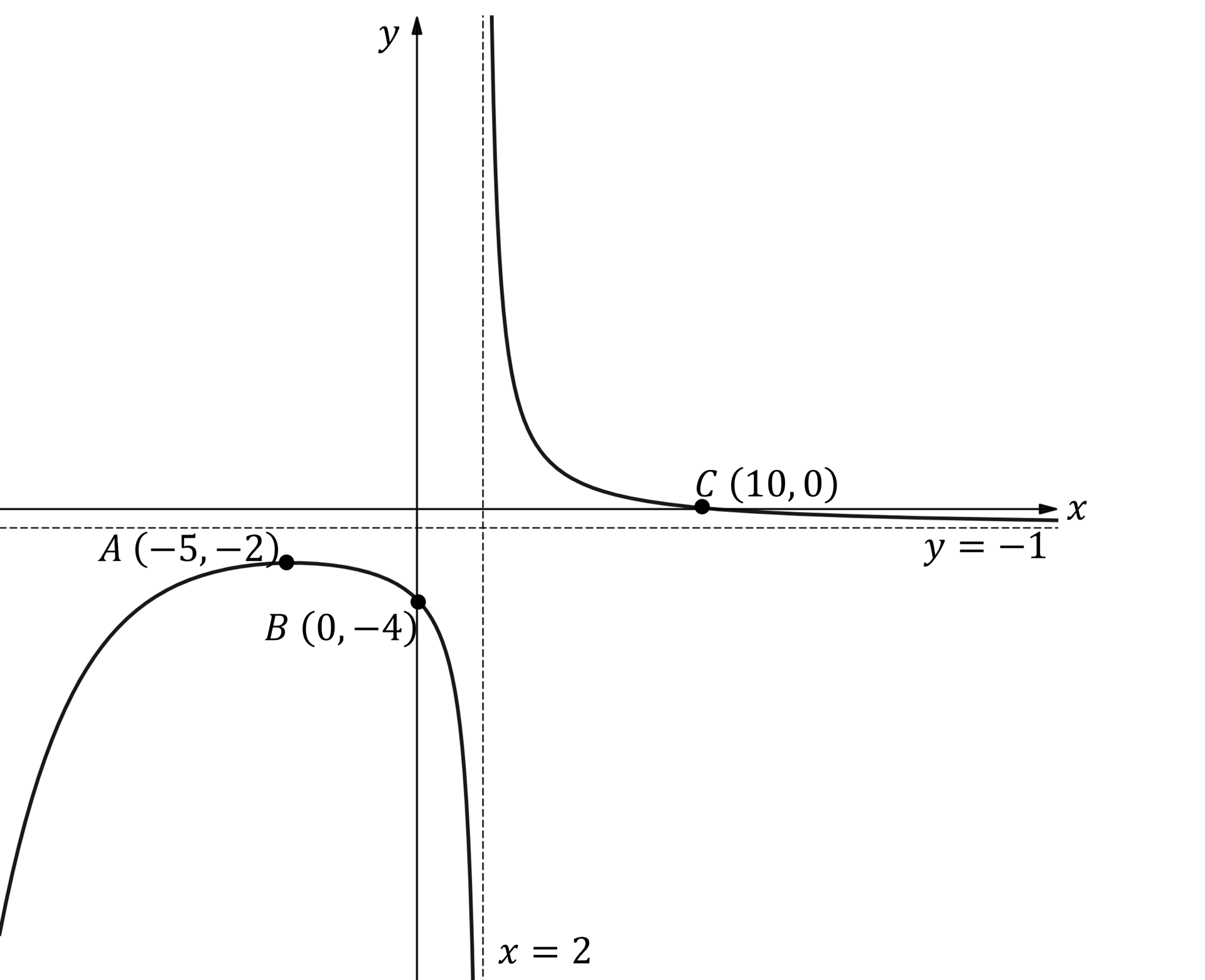
2-9-2-we-image

Sketch the graph of . $y = \frac{1}{f (x)}$ .

2-9-2-ib-aa-hl-reciprocal-trans-we-solution

Square Transformations

What effects do square transformations have on the graphs?

The effects are similar to the transformation y = |f(x)|

The parts below the x-axis are reflected
The vertical distance between a point and the x-axis is squared

This has the effect of smoothing the curve at the x-axis

$y = {[f (x)]}^{2}$ is never below the x-axis
The x-coordinates stay the same
The y-coordinates change

Their values are squared

The coordinates (x, y) become (x, y²)

Points that lie on the x-axis or the line y = 1 stay the same

How do I sketch the graph of the square of a function: y = [f(x)]²?

Sketch the square transformation by considering the different features of the original graph
Consider key points on the original graph

If (x₁, y₁) is a point on y = f(x)

$(x_{1}, {y_{1}}^{2})$ is a point on $y = {[f (x)]}^{2}$
If |y₁|< 1 then the point gets closer to the x-axis
If |y₁|> 1 then the point gets further away from the x-axis

If y = f(x) has a y-intercept at (0, c)

The square graph $y = {[f (x)]}^{2}$ has a y-intercept at $(0, c^{2})$

If y = f(x) has a root at (a, 0)

The square graph $y = {[f (x)]}^{2}$ has a root and turning point at (a, 0)

If y = f(x) has a vertical asymptote at $x = a$

The square graph $y = {[f (x)]}^{2}$ has a vertical asymptote at $x = a$

If y = f(x) has a local maximum at (x₁, y₁)

The square graph $y = {[f (x)]}^{2}$ has a local maximum at (x₁, y₁²) if y₁> 0
The square graph $y = {[f (x)]}^{2}$ has a local minimum at (x₁, y₁²) if y₁≤ 0

If y = f(x) has a local minimum at (x₁, y₁)

The square graph $y = {[f (x)]}^{2}$ has a local minimum at (x₁, y₁²) if y₁≥ 0
The square graph $y = {[f (x)]}^{2}$ has a local maximum at (x₁, y₁²) if y₁< 0

Exam Tip

In an exam question when sketching $y = {[f (x)]}^{2}$ make it clear that the points where the new graph touches the x-axis are smooth
- This will make it clear to the examiner that you understand the difference between the roots of the graphs $y = |f (x)|$ and $y = {[f (x)]}^{2}$

Worked Example

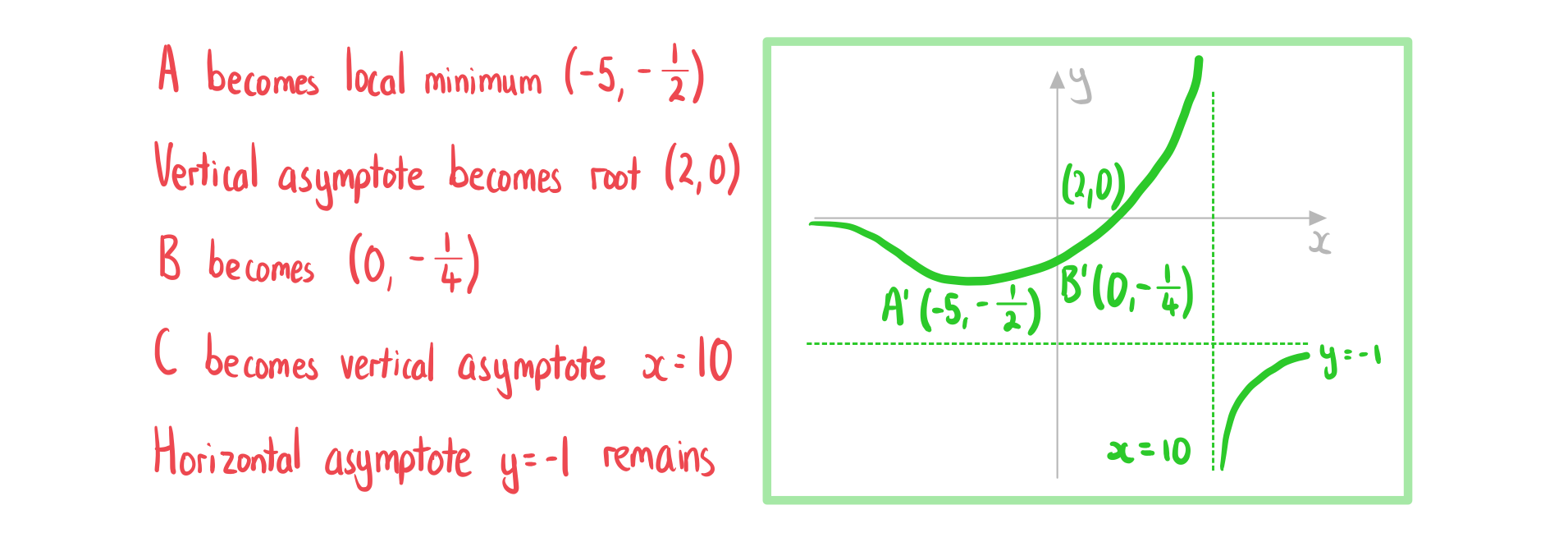
The diagram below shows the graph of $y = f (x)$ which has a local maximum at the point A.

2-9-2-we-image

Sketch the graph of $y = {[f (x)]}^{2}$ .

2-9-2-ib-aa-hl-square-trans-we-solution

DP IB Maths: AA HL

Revision Notes

2.9.4 Reciprocal & Square Transformations

Reciprocal Transformations

What effects do reciprocal transformations have on the graphs?

How do I sketch the graph of the reciprocal of a function: y = 1/f(x)?

Worked Example

Square Transformations

What effects do square transformations have on the graphs?

How do I sketch the graph of the square of a function: y = [f(x)]²?

Exam Tip

Worked Example

Author: Daniel

Resources

Members

Company

Quick Links