5.9.4 Advanced Applications of Integration

What is meant by the area between a curve and the y-axis?

• The area referred to is the region bounded by
• the graph of 
• the -axis
• the horizontal line 
• the horizontal line 
• The exact area can be found by evaluating a definite integral
• The graph of could be a straight line
• using basic shape area formulae may be easier than integration
• e.g. area of a trapezium: 

How do I find the area between a curve and the y-axis?

• Use the formula

• This is given in the formula booklet
• The function is normally given in the form 
• so will need rearranging into the form 
•  and may not be given directly as could involve the -axis () and/or a root of
• use a GDC to plot the curve, sketch it and highlight the area to help

STEP 1
Identify the limits  and 
Sketch the graph of or use a GDC to do so, especially if and are not given directly in the question

STEP 2
Rearrange  into the form
This is similar to finding the inverse function

STEP 3
Evaluate the formula to evaluate the integral and find the area required
If using a GDC remember to include the modulus ( | … | ) symbols around  

• In trickier problems some (or all) of the area may be ‘negative’
  • this will be any area that is left of the -axis (negative -values)
  • || makes such areas ‘positive’
    • a GDC will apply ‘||’ automatically as long as the | … | are included
    • otherwise, to apply ‘||’, split the integral into positive and negative parts; write an integral and evaluate each part separately and add the modulus of each part together to give the total area

What is a volume of revolution around the x-axis?

• A solid of revolution is formed when an area bounded by a function
  (and other boundary equations) is rotated radians around the -axis
• The volume of revolution is the volume of this solid

• Be careful – the ’front’ and ‘back’ of this solid are flat
  • they were created from straight (vertical) lines
  • 3D sketches can be misleading

How do I solve problems involving the volume of revolution around x-axis?

• Use the formula

• This is given in the formula booklet
• is a function of
• and are the equations of the (vertical) lines bounding the area
  • If and are not stated in a question, the boundaries could involve the -axis () and/or a root of
  • Use a GDC to plot the curve, sketch it and highlight the area to help
• Visualising the solid created is helpful
  • Try sketching some functions and their solids of revolution to help

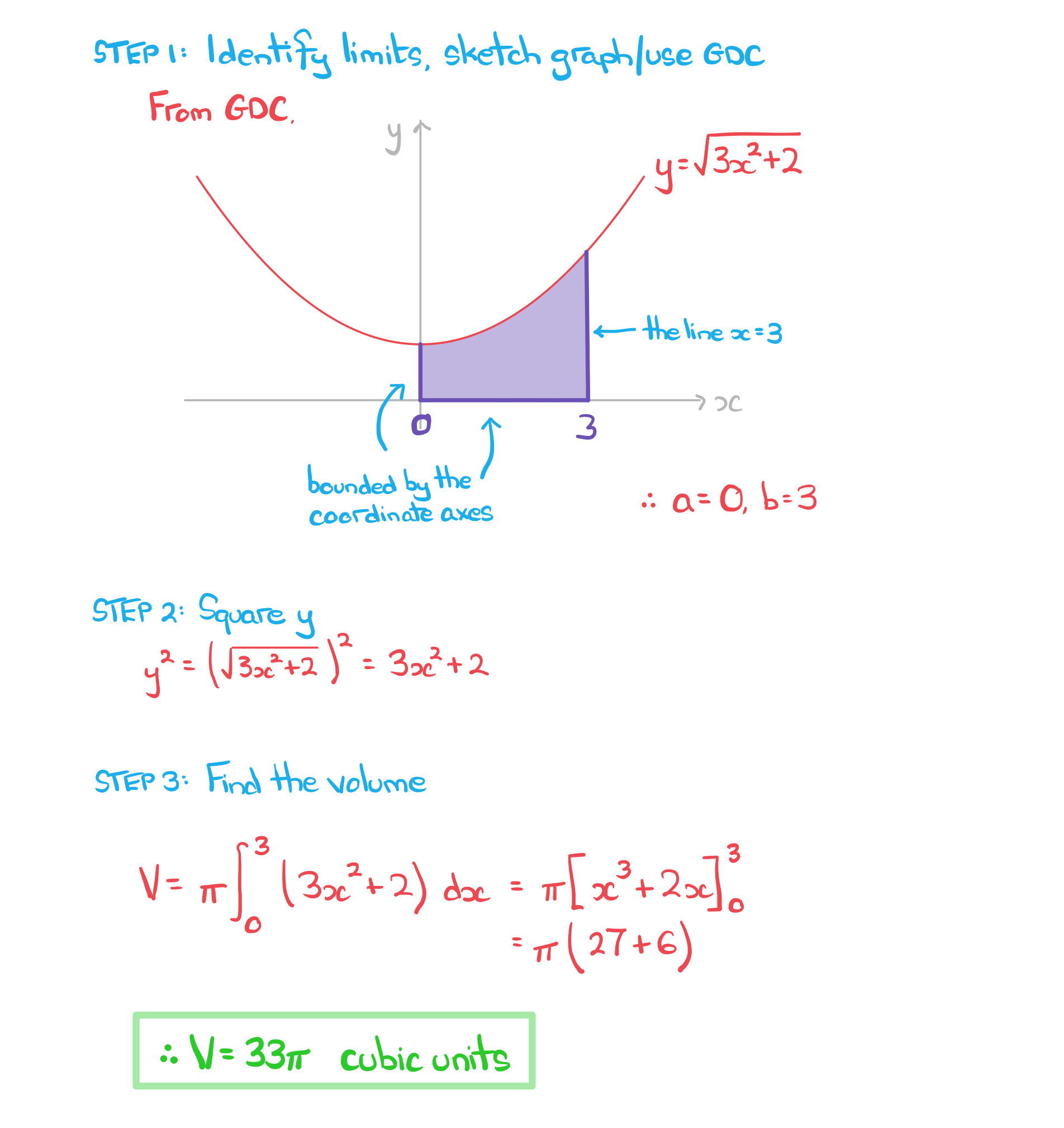
STEP 1
Identify the limits and
Sketching the graph of or using a GDC to do so is helpful, especially when  and are not given directly in the question

STEP 2
Square

STEP 3
Use the formula to evaluate the integral and find the volume of revolution
An answer may be required in exact form

What is a volume of revolution around the y-axis?

• Very similar to above, this is a solid of revolution which is formed when an area bounded by a function (and other boundary equations) is rotated radians  around the -axis
• The volume of revolution is the volume of this solid

How do I solve problems involving the volume of revolution around y-axis?

• Use the formula

• This is given in the formula booklet
• The function is usually given in the form 
  • so will need rearranging into the form
• and  may not be given directly as could involve the -axis () and/or a root of
  • Use a GDC to plot the curve, sketch it and highlight the area to help
• Visualising the solid created is helpful

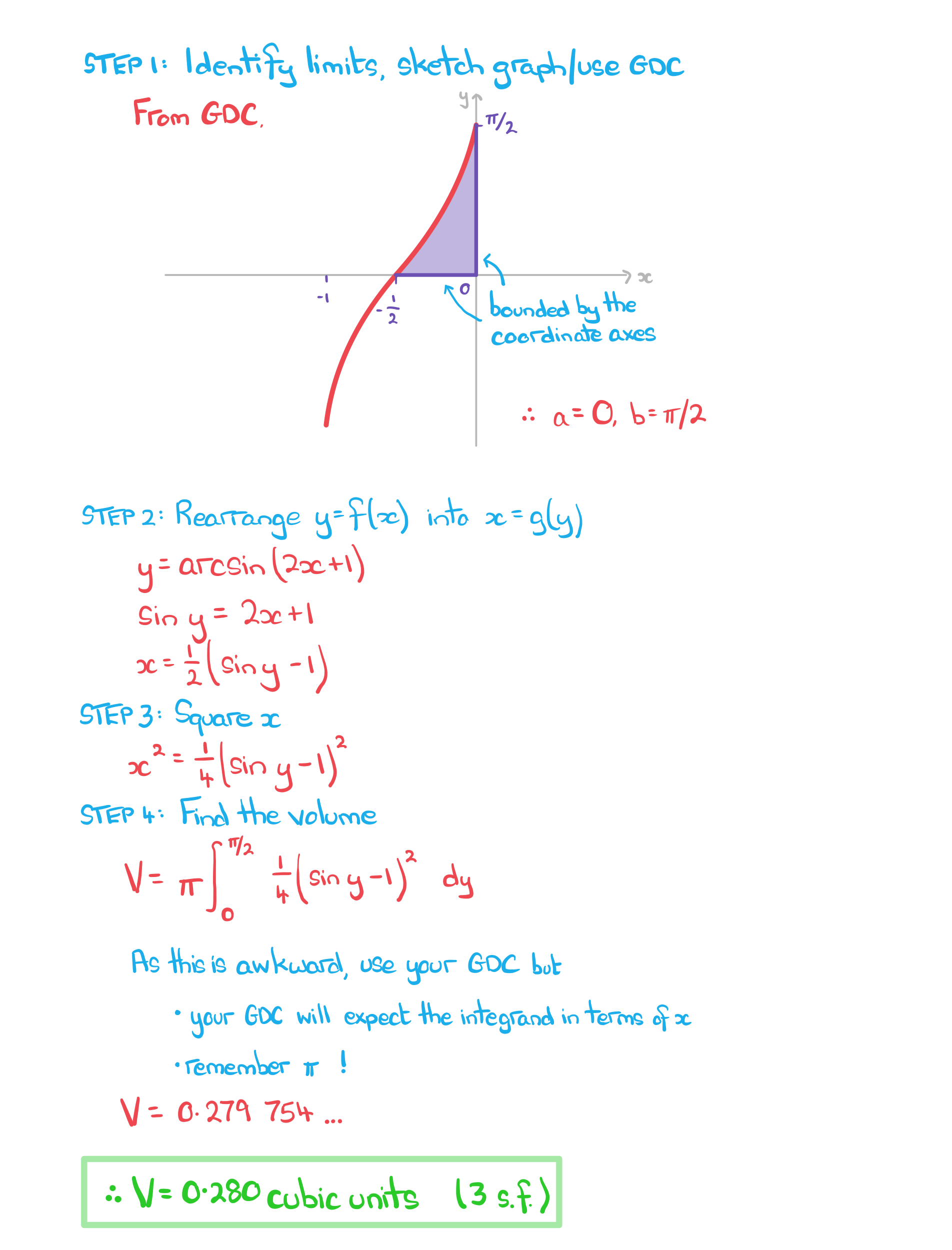
STEP 1
Identify the limits and 
Sketching the graph of or using a GDC to do so is helpful, especially if and  are not given directly in the question

STEP 2
Rearrange into the form 
This is similar to finding the inverse function

STEP 3
Square

STEP 4
Use the formula to evaluate the integral and find the volume of revolution
An answer may be required in exact form