3.6.2 Compound Angle Formulae

What are the compound angle formulae?

• There are six compound angle formulae (also known as addition formulae), two each for sin, cos and tan:
• For sin the +/- sign on the left-hand side matches the one on the right-hand side
  • sin(A+B)≡sinAcosB + cosAsinB
  • sin(A-B)≡sinAcosB - cosAsinB

• For cos the +/- sign on the left-hand side is opposite to the one on the right-hand side
  • cos(A+B)≡cosAcosB - sinAsinB
  • cos(A-B)≡cosAcosB + sinAsinB

• For tan the +/- sign on the left-hand side matches the one in the numerator on the right-hand side, and is opposite to the one in the denominator
  • 
  • 

• The compound angle formulae can all the found in the formula booklet, you do not need to remember them

When are the compound angle formulae used?

• The compound angle formulae are particularly useful when find the values of trigonometric ratios without the use of a calculator
• For example to find the value of sin15° rewrite it as sin (45 – 30)° and then
• apply the compound formula for sin(A – B)
• use your knowledge of exact values to calculate the answer
• The compound angle formulae are also used…
• … to derive further multiple angle trig identities such as the double angle formulae
• … in trigonometric proof
• … to simplify complicated trigonometric equations before solving

How are the compound angle formulae for cosine proved?

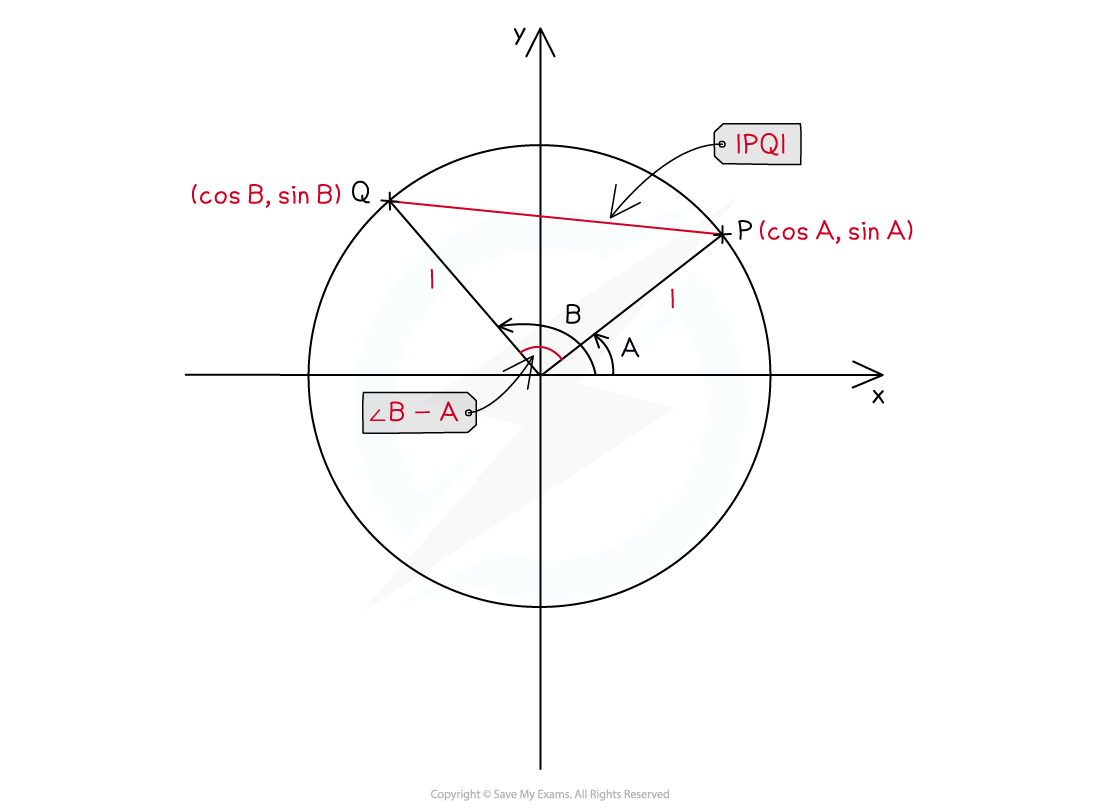
• The proof for the compound angle identity cos (A – B ) = cos A cos B  + sin A sin B can be seen by considering two coordinates on a unit circle, P (cos A, sin A) and Q (cos B, sin B )
• The angle between the positive x- axis and the point P is A
• The angle between the positive x- axis and the point Q is B
• The angle between P and Q is B – A

• Using the distance formula (Pythagoras) the distance PQ can be given as
• |PQ|² = (cos A – cos B)² + (sin A – sin B)²
• Using the cosine rule the distance PQ can be given as
• |PQ|²  =  1² + 1² -2(1)(1)cos(B – A) = 2 - 2 cos(B – A)
• Equating these two formulae, expanding and rearranging gives
• 2 - 2 cos(B – A) = cos²A + sin²A + cos²B + sin²B –2 cos A cos B  - 2sin A sin B
• 2 - 2 cos(B – A) = 2 – 2(cos A cos B  + sin A sin B )
• Therefore cos (B – A) = cos A cos B  + sin A sin B
• Changing -A for A in this identity and rearranging proves the identity for cos (A + B)
• cos (B – (-A)) = cos(-A) cos B  + sin(-A) sin B =  cos A cos B – sin A sin B

How are the compound angle formulae for sine proved?

• The proof for the compound angle identity sin (A + B ) can be seen by using the above proof for cos (B – A) and
• Considering cos (π/2 – (A + B)) = cos (π/2)cos(A + B) + sin(π/2)sin(A + B)
• Therefore cos (π/2 – (A + B)) = sin(A + B)
• Rewriting cos (π/2 – (A + B)) as cos ((π/2 – A) + B) gives
• cos (π/2 – (A + B)) = cos (π/2 – A) cos B + sin (π/2 – A) sin B
• Using cos (π/2 – A) = sin A and sin (π/2 – A) = cos A and equating gives
• sin (A + B) = sin A cos B + cos A cos B
• Substituting B for -B proves the result for sin (A – B)

How are the compound angle formulae for tan proved?

• The proof for the compound angle identities tan (A ± B) can be seen by
• Rewriting tan (A ± B ) as 
• Substituting the compound angle formulae in
• Dividing the numerator and denominator by cos A cos B