Reciprocal Functions & Graphs
What is the reciprocal function?
- The reciprocal function is defined by
- Its domain is the set of all real values except 0
- Its range is the set of all real values except 0
- The reciprocal function has a self-inverse nature
What are the key features of the reciprocal graph?
- The graph does not have a y-intercept
- The graph does not have any roots
- The graph has two asymptotes
- A horizontal asymptote at the x-axis:
- This is the limiting value when the absolute value of x gets very large
- A vertical asymptote at the y-axis:
- This is the value that causes the denominator to be zero
- A horizontal asymptote at the x-axis:
- The graph has two axes of symmetry
- The graph does not have any minimum or maximum points
Linear Rational Functions & Graphs
What is a rational function with linear terms?
- A (linear) rational function is of the form
- Its domain is the set of all real values except
- Its range is the set of all real values except
- The reciprocal function is a special case of a rational function
What are the key features of linear rational graphs?
- The graph has a y-intercept at
provided
- The graph has one root at
provided
- The graph has two asymptotes
- A horizontal asymptote:
- This is the limiting value when the absolute value of x gets very large
- A vertical asymptote:
- This is the value that causes the denominator to be zero
- A horizontal asymptote:
- The graph does not have any minimum or maximum points
- If you are asked to sketch or draw a rational graph:
- Give the coordinates of any intercepts with the axes
- Give the equations of the asymptotes
Exam Tip
- If you draw a horizontal line anywhere it should only intersect this type of graph once at most
- The only horizontal line that should not intersect the graph is the horizontal asymptote
- This can be used to check your sketch in an exam
Worked Example
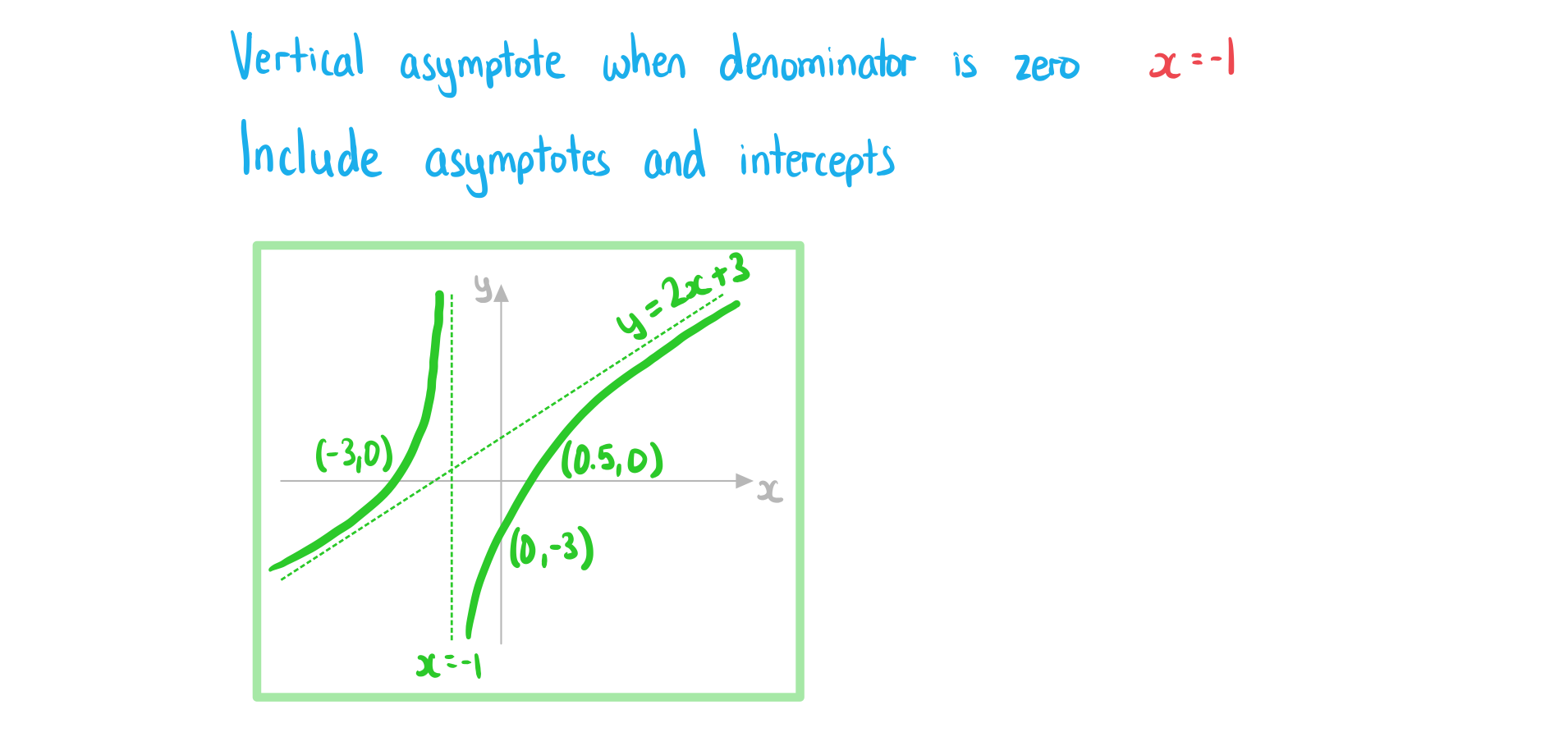
The function is defined by
for
.
a)
Write down the equation of
(i)
the vertical asymptote of the graph of  ,
,
(ii)
the horizontal asymptote of the graph of  .
.

b)
Find the coordinates of the intercepts of the graph of  with the axes.
with the axes.
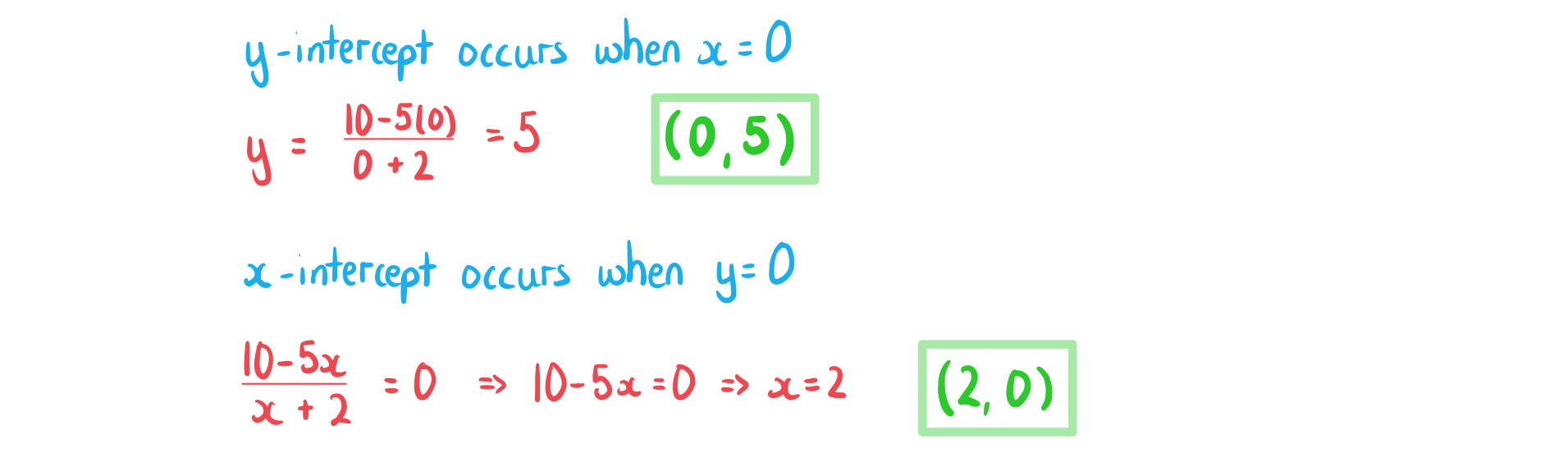
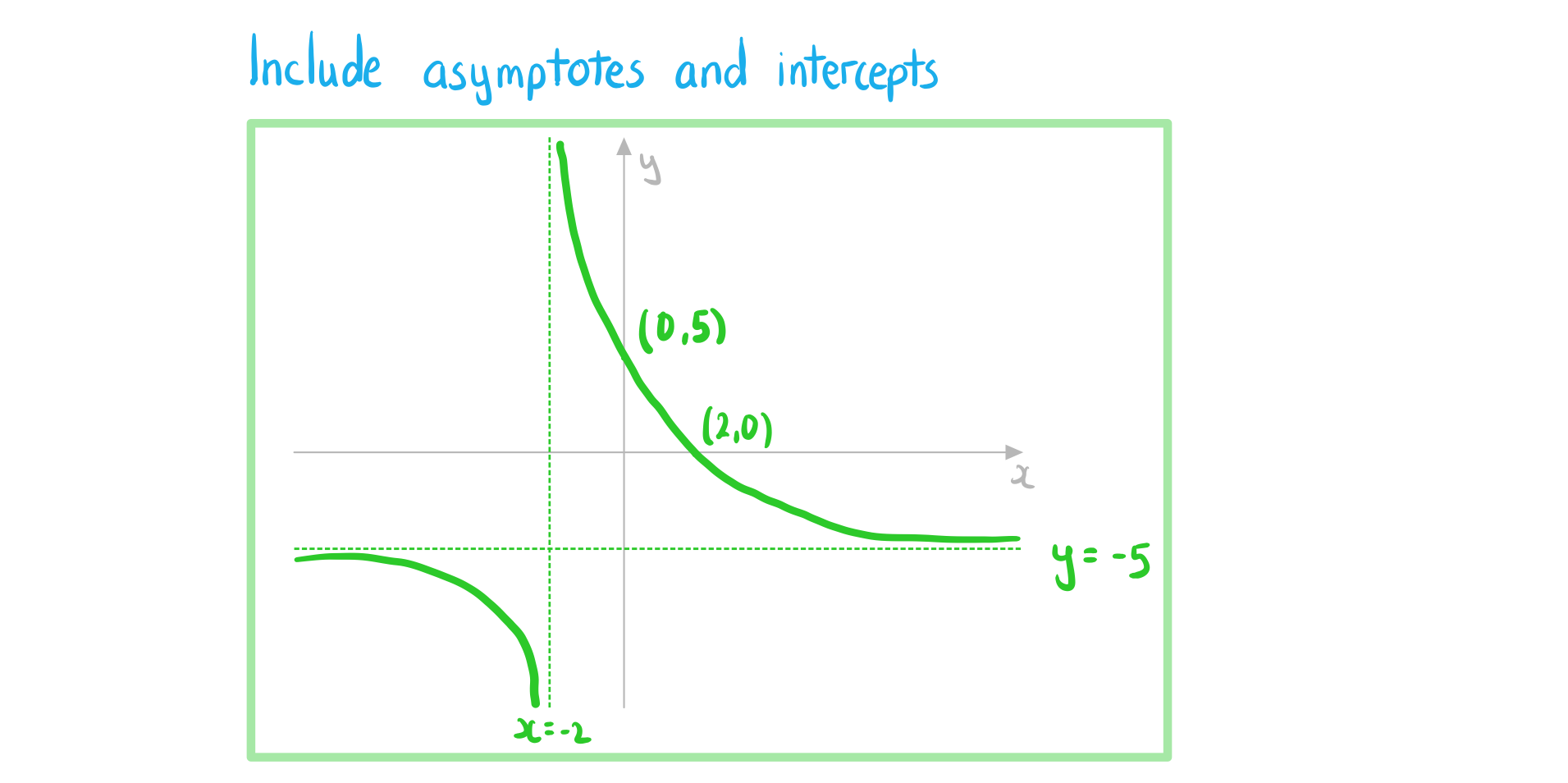
c)
Sketch the graph of  .
.
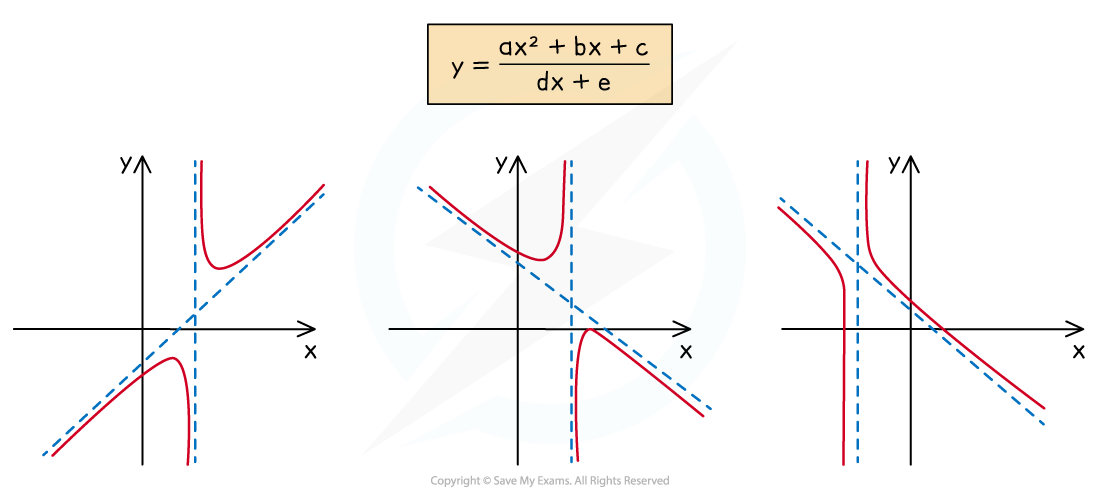
Quadratic Rational Functions & Graphs
How do I sketch the graph of a rational function where the terms are not linear?
- A rational function can be written
- Where g and h are polynomials
- To find the y-intercept evaluate
- To find the x-intercept(s) solve
- To find the equations of the vertical asymptote(s) solve
- There will also be an asymptote determined by what f(x) tends to as x approaches infinity
- In this course it will be either:
- Horizontal
- Oblique (a slanted line)
- This can be found by writing
in the form
- You can do this by polynomial division or comparing coefficients
- The function then tends to the curve
What are the key features of rational graphs: quadratic over linear?
- For the rational function of the form
- The graph has a y-intercept at
provided
- The graph can have 0, 1 or 2 roots
- They are the solutions to
- The graph has one vertical asymptote
- The graph has an oblique asymptote
- Which can be found by writing
in the form
- Where p, q, r are constants
- This can be done by polynomial division or comparing coefficients
What are the key features of rational graphs: linear over quadratic?
- For the rational function of the form
- The graph has a y-intercept at
provided
- The graph has one root at
- The graph has can have 0, 1 or 2 vertical asymptotes
- They are the solutions to
- The graph has a horizontal asymptote
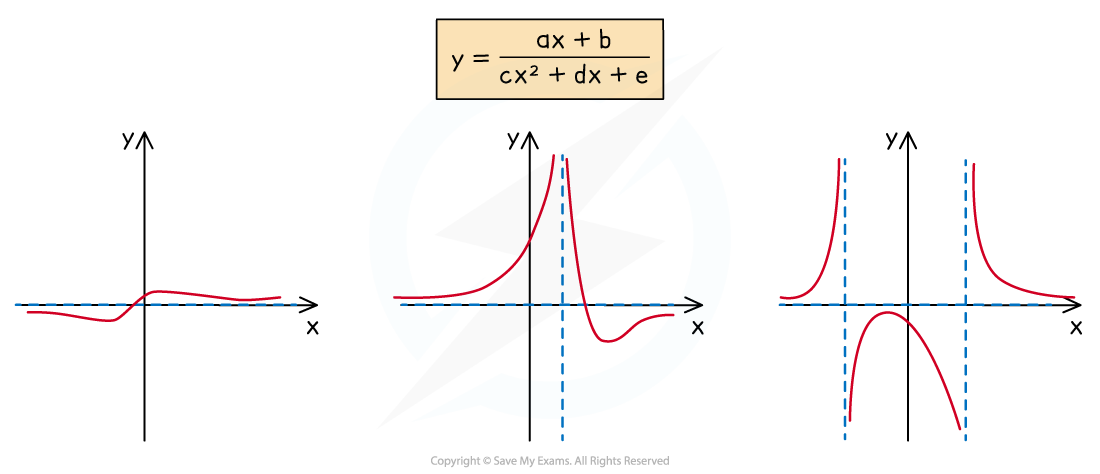
Exam Tip
- If you draw a horizontal line anywhere it should only intersect this type of graph twice at most
- This idea can be used to check your graph or help you sketch it
Worked Example
The function is defined by
for
.
a)
(i)
Show that format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Cline%20stroke%3D%22%23000000%22%20stroke-linecap%3D%22square%22%20stroke-width%3D%221%22%20x1%3D%222.5%22%20x2%3D%2293.5%22%20y1%3D%2224.5%22%20y2%3D%2224.5%22%2F%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%228.5%22%20y%3D%2217%22%3E2%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2217.5%22%20y%3D%2217%22%3Ex%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2213%22%20text-anchor%3D%22middle%22%20x%3D%2226.5%22%20y%3D%2212%22%3E2%3C%2Ftext%3E%3Ctext%20font-family%3D%22math16a33855ddb1fea6678da29e5e0%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2238.5%22%20y%3D%2217%22%3E%2B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%2251.5%22%20y%3D%2217%22%3E5%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2260.5%22%20y%3D%2217%22%3Ex%3C%2Ftext%3E%3Ctext%20font-family%3D%22math16a33855ddb1fea6678da29e5e0%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2274.5%22%20y%3D%2217%22%3E%26%23x2212%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%2287.5%22%20y%3D%2217%22%3E3%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2234.5%22%20y%3D%2242%22%3Ex%3C%2Ftext%3E%3Ctext%20font-family%3D%22math16a33855ddb1fea6678da29e5e0%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2248.5%22%20y%3D%2242%22%3E%2B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%2261.5%22%20y%3D%2242%22%3E1%3C%2Ftext%3E%3Ctext%20font-family%3D%22math16a33855ddb1fea6678da29e5e0%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22104.5%22%20y%3D%2231%22%3E%3D%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22117.5%22%20y%3D%2231%22%3Ep%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22126.5%22%20y%3D%2231%22%3Ex%3C%2Ftext%3E%3Ctext%20font-family%3D%22math16a33855ddb1fea6678da29e5e0%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22140.5%22%20y%3D%2231%22%3E%2B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22153.5%22%20y%3D%2231%22%3Eq%3C%2Ftext%3E%3Ctext%20font-family%3D%22math16a33855ddb1fea6678da29e5e0%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22167.5%22%20y%3D%2231%22%3E%2B%3C%2Ftext%3E%3Cline%20stroke%3D%22%23000000%22%20stroke-linecap%3D%22square%22%20stroke-width%3D%221%22%20x1%3D%22178.5%22%20x2%3D%22217.5%22%20y1%3D%2224.5%22%20y2%3D%2224.5%22%2F%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22198.5%22%20y%3D%2217%22%3Er%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22184.5%22%20y%3D%2242%22%3Ex%3C%2Ftext%3E%3Ctext%20font-family%3D%22math16a33855ddb1fea6678da29e5e0%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22198.5%22%20y%3D%2242%22%3E%2B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%22211.5%22%20y%3D%2242%22%3E1%3C%2Ftext%3E%3C%2Fsvg%3E) for constants
for constants format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%224.5%22%20y%3D%2216%22%3Ep%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1f7177163c833dff4b38fc8d287%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2212.5%22%20y%3D%2216%22%3E%2C%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2223.5%22%20y%3D%2216%22%3Eq%3C%2Ftext%3E%3C%2Fsvg%3E) and
and  which are to be found.
which are to be found.
(ii)
Hence write down the equation of the oblique asymptote of the graph of  .
.

b)
Find the coordinates of the intercepts of the graph of  with the axes.
with the axes.

c)
Sketch the graph of  .
.