Shortest Distance Between a Line and a Plane
How do I find the shortest distance between a given point on a line and a plane?
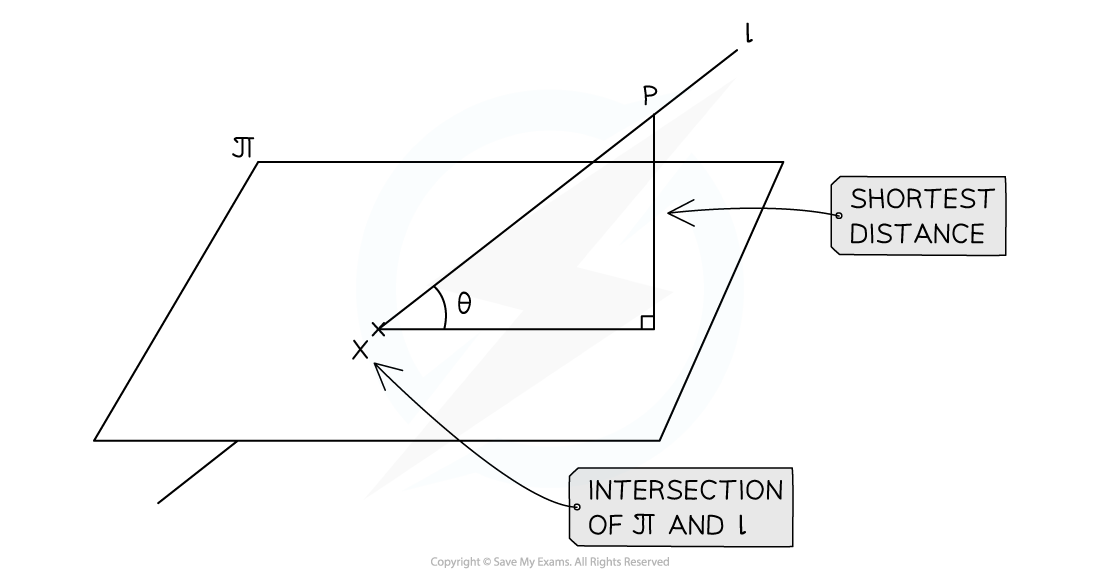
- The shortest distance from any point on a line to a plane will always be the perpendicular distance from the point to the plane
- Given a point, P, on the line
with equation
and a plane
with equation
- STEP 1: Find the vector equation of the line perpendicular to the plane that goes through the point, P, on
- This will have the position vector of the point, P, and the direction vector n
- STEP 2: Find the coordinates of the point of intersection of this new line with
by substituting the equation of the line into the equation of the plane
- STEP 3: Find the distance between the given point on the line and the point of intersection
- This will be the shortest distance from the plane to the point
- STEP 1: Find the vector equation of the line perpendicular to the plane that goes through the point, P, on
- A question may provide the acute angle between the line and the plane
- Use right-angled trigonometry to find the perpendicular distance between the point on the line and the plane
- Drawing a clear diagram will help
- Use right-angled trigonometry to find the perpendicular distance between the point on the line and the plane
How do I find the shortest distance between a plane and a line parallel to the plane?
- The shortest distance between a line and a plane that are parallel to each other will be the perpendicular distance from the line to the plane
- Given a line
with equation
and a plane
parallel to
with equation
- Where n is the normal vector to the plane
- STEP 1: Find the equation of the line
perpendicular to
and
going through the point a in the form
- STEP 2: Find the point of intersection of the line
and
- STEP 3: Find the distance between the point of intersection and the point,

Exam Tip
- Vector planes questions can be tricky to visualise, read the question carefully and sketch a very simple diagram to help you get started
Worked Example
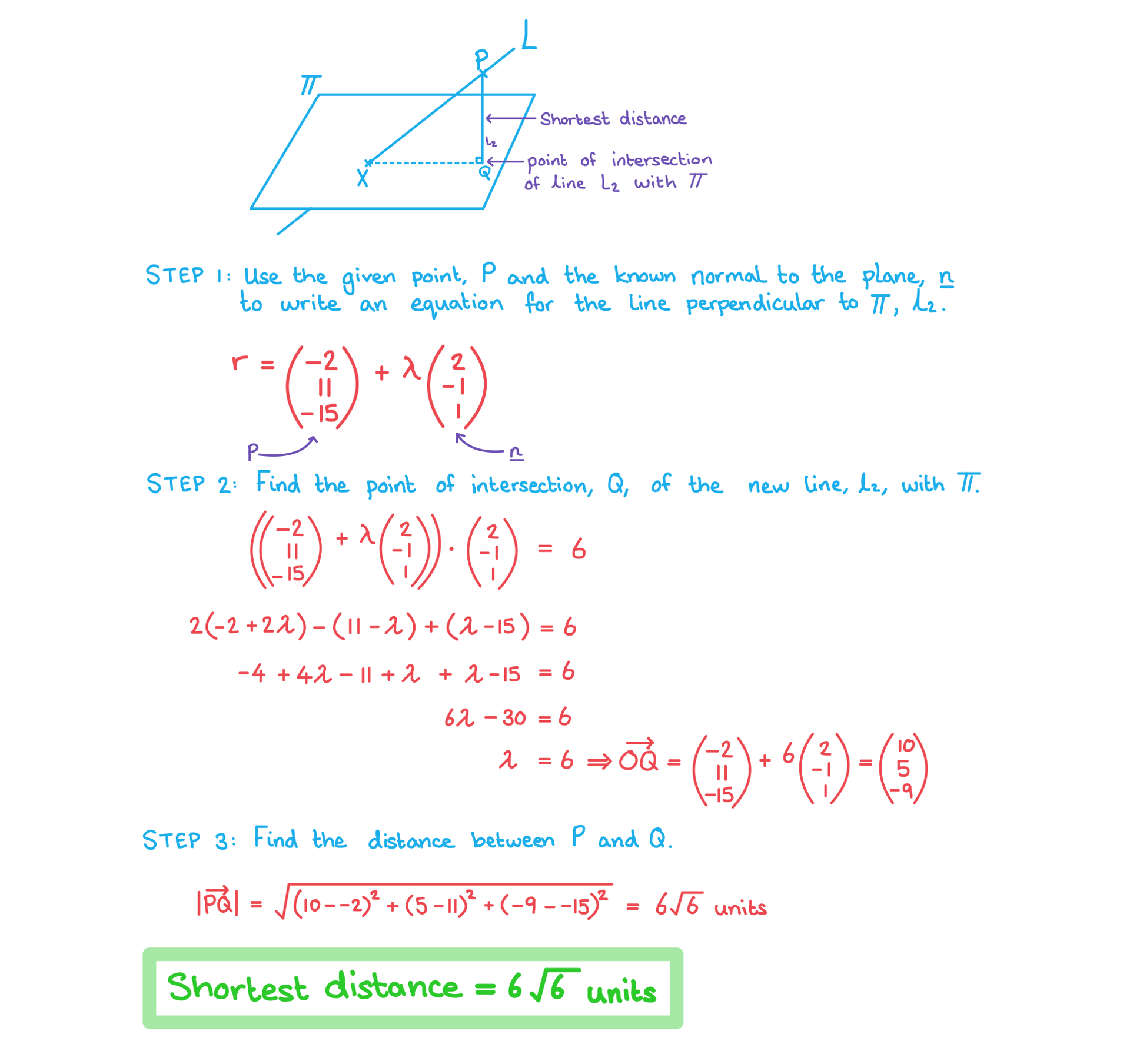
The plane has equation
.
The line has equation
.
The point lies on the line
.
Find the shortest distance between the point P and the plane .
Shortest Distance Between Two Planes
How do I find the shortest distance between two parallel planes?
- Two parallel planes will never intersect
- The shortest distance between two parallel planes will be the perpendicular distance between them
- Given a plane
with equation
and a plane
with equation
then the shortest distance between them can be found
- STEP 1: The equation of the line perpendicular to both planes and through the point a can be written in the form r = a + sn
- STEP 2: Substitute the equation of the line into
to find the coordinates of the point where the line meets
- STEP 3: Find the distance between the two points of intersection of the line with the two planes
How do I find the shortest distance from a given point on a plane to another plane?
- The shortest distance from any point, P on a plane,
, to another plane,
will be the perpendicular distance from the point to
- STEP 1: Use the given coordinates of the point P on
and the normal to the plane
to find the vector equation of the line through P that is perpendicular to
- STEP 2: Find the point of intersection of this line with the plane
- STEP 3: Find the distance between the two points of intersection
Exam Tip
- There are a lot of steps when answering these questions so set your methods out clearly in the exam
Worked Example
Consider the parallel planes defined by the equations:
,
.
Find the shortest distance between the two planes and
.

