| Date | November 2011 | Marks available | 2 | Reference code | 11N.2.sl.TZ0.6 |
| Level | SL | Paper | 2 | Time zone | TZ0 |
| Command term | State and explain | Question number | 6 | Adapted from | N/A |
Question
Consider the following equilibrium:
\[\begin{array}{*{20}{l}} {{\text{4N}}{{\text{H}}_3}{\text{(g)}} + {\text{5}}{{\text{O}}_2}{\text{(g)}} \rightleftharpoons {\text{4NO(g)}} + {\text{6}}{{\text{H}}_2}{\text{O(g)}}}&{\Delta {H^\Theta } = - 909{\text{ kJ}}} \end{array}\]
Nitrogen reacts with hydrogen to form ammonia in the Haber process, according to the following equilibrium.
\[\begin{array}{*{20}{l}} {{{\text{N}}_{\text{2}}}{\text{(g)}} + {\text{3}}{{\text{H}}_{\text{2}}}{\text{(g)}} \rightleftharpoons {\text{2N}}{{\text{H}}_{\text{3}}}{\text{(g)}}}&{\Delta {H^\Theta } = - 92.6{\text{ kJ}}} \end{array}\]
Deduce the equilibrium constant expression, \({K_{\text{c}}}\), for the reaction.
Predict the direction in which the equilibrium will shift when the following changes occur.
The volume increases.
The temperature decreases.
\({{\text{H}}_{\text{2}}}{\text{O(g)}}\) is removed from the system.
A catalyst is added to the reaction mixture.
Define the term activation energy, \({E_{\text{a}}}\).
Nitrogen monoxide, NO, is involved in the decomposition of ozone according to the following mechanism.
\[\begin{array}{*{20}{l}} {}&{{{\text{O}}_{\text{3}}} \to {{\text{O}}_{\text{2}}} + {\text{O}} \bullet } \\ {}&{{{\text{O}}_3} + {\text{NO}} \to {\text{N}}{{\text{O}}_2} + {{\text{O}}_2}} \\ {}&{{\text{N}}{{\text{O}}_2} + {\text{O}} \bullet \to {\text{NO}} + {{\text{O}}_2}} \\ {{\text{Overall:}}}&{{\text{2}}{{\text{O}}_3} \to {\text{3}}{{\text{O}}_2}} \end{array}\]
State and explain whether or not NO is acting as a catalyst.
Define the term endothermic reaction.
Sketch the Maxwell-Boltzmann energy distribution curve for a reaction with and without a catalyst, and label both axes.
Define the term rate of reaction.
Iron, used as the catalyst in the Haber process, has a specific heat capacity of \({\text{0.4490 J}}\,{{\text{g}}^{ - 1}}{{\text{K}}^{ - 1}}\). If 245.0 kJ of heat is supplied to 8.500 kg of iron, initially at a temperature of 15.25 °C, determine its final temperature in K.
Markscheme
\({\text{(}}{K_{\text{c}}}{\text{)}} = \frac{{{{{\text{[NO]}}}^4}{{{\text{[}}{{\text{H}}_2}{\text{O]}}}^6}}}{{{{{\text{[N}}{{\text{H}}_3}{\text{]}}}^4}{{{\text{[}}{{\text{O}}_2}{\text{]}}}^5}}}\);
No mark if square brackets are omitted or are incorrect.
right;
right;
right;
no change;
minimum energy needed (by reactants/colliding particles) to react/start/initiate a reaction;
Allow energy difference between reactants and transition state.
catalyst;
regenerated at end of reaction / OWTTE;
(system) absorbs/takes in heat from surroundings / OWTTE;
Allow standard enthalpy change/ \(\Delta {H^\Theta }\) positive.
Allow bond breaking more energetic then bond formation / OWTTE.
Absorbs/takes in heat alone not sufficient for mark.
Curve showing:
general shape of Maxwell-Boltzmann energy distribution curve;
correct position of \({E_{\text{a}}}\) (catalysed) and \({E_{\text{a}}}\) (uncatalysed);
labelled y-axis: probability of particles (with that kinetic energy) and labelled x-axis: (kinetic) energy;
Allow number/fraction/proportion of particles (with kinetic energy) for y-axis label, but do not allow amount or particles.
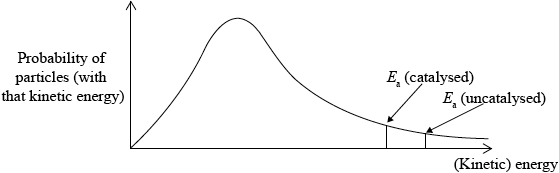
Award [2 max] if a second curve is drawn, but at a higher temperature, M2 will not be scored here.
change in concentration of reactant/product with time / rate of change of concentration;
Increase can be used instead of change for product or decrease can be used instead of change for reactant.
Allow mass/amount/volume instead of concentration.
Do not accept substance.
\(q = mc\Delta T = 2.450 \times {10^5} = (8.500 \times {10^3})(0.4490)({T_{\text{f}}} - 15.25)\);
\({T_{\text{f}}} = 79.44{\text{ °C}}/\Delta T = 64.19{\text{ (°C}}/{\text{K)}}\);
\({T_{\text{f}}} = (79.44 + 273) = 352{\text{ (K)}}\);
Award [3] for correct final answer.
Accept the use of 273.15 K instead of 273 K giving final value of 352.59 K.
For M1 and M2 award [1 max] for use of \(q = mc\Delta T\) if incorrect units of m and c are used.
Examiners report
In part (a) of this question the \({K_{\text{c}}}\) expression was usually written correctly though the very weak students did mix up the numerator and denominator in (i), or include a + sign between substances.
Candidates generally had few problems, but the reaction condition that proved to be the most the most difficult factor was the volume.
Activation energy was often clearly defined though some forgot to mention minimum.
The best students realised that NO acted as a catalyst as it was regenerated at the end of the reaction. However many weaker students stated it was not a catalyst as it was not involved in the reaction.
The definition of an endothermic reaction was generally well answered, however some just said it absorbs heat and forgot to mention the surroundings in their answer.
Incorrect labels for the axes were often seen, as well as a very high proportion of symmetrical curves, some which did not start at the origin. Also many drew two curves. Also in some cases the catalyzed and uncatalyzed activation energies were often mixed up. The weaker students drew an enthalpy level diagram instead of a Maxwell-Boltzmann distribution.
In the definition for rate of reaction some students forgot to mention concentration.

