| Date | November 2011 | Marks available | 2 | Reference code | 11N.2.hl.TZ0.6 |
| Level | HL | Paper | 2 | Time zone | TZ0 |
| Command term | Compare | Question number | 6 | Adapted from | N/A |
Question
Consider the structure and bonding in \({\text{MgC}}{{\text{l}}_{\text{2}}}\) and \({\text{PC}}{{\text{l}}_{\text{5}}}\).
For each of the species \({\text{PB}}{{\text{r}}_{\text{3}}}\) and \({\text{S}}{{\text{F}}_{\text{6}}}\):
State and explain the difference in the electrical conductivity in the liquid state of the two chlorides.
(i) deduce the Lewis structure.
(ii) predict the shape and bond angle.
(iii) predict and explain the molecular polarity.

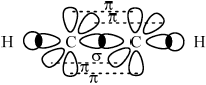
Compare the formation of sigma (\(\sigma \)) and pi (\(\pi \)) bonds between the carbon atoms in a molecule of ethyne.
Markscheme
\({\text{MgC}}{{\text{l}}_2}\) conducts and \({\text{PC}}{{\text{l}}_5}\) does not;
\({\text{MgC}}{{\text{l}}_2}\) ionic and \({\text{PC}}{{\text{l}}_5}\) covalent/molecular/(consists of) molecules;
Award [1 max] for MgCl2 conducts and ionic.
Award [1 max] for PCl5 does not conduct and covalent/molecular/(consists of molecules).
ions can move in liquid (in \({\text{MgC}}{{\text{l}}_2}\)) / OWTTE;
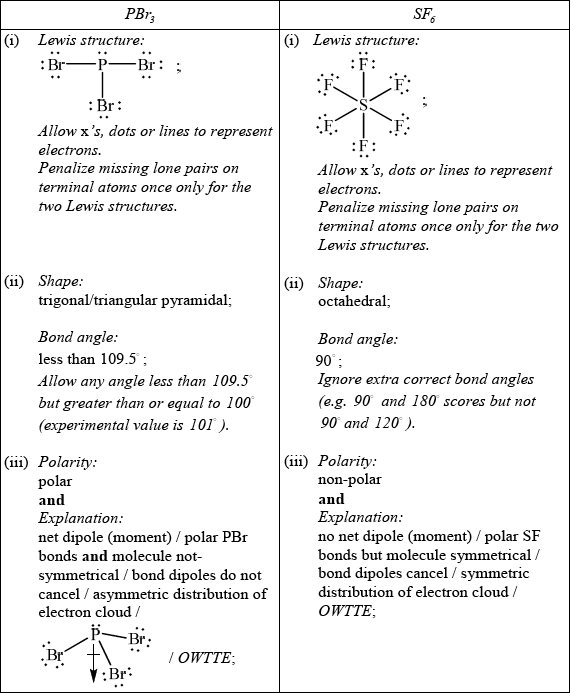
Do not allow ECF in this question from incorrect Lewis structure.
Allow [1 max] for stating that PBr3 is polar and SF6 is non-polar without giving a reason or if explanations are incorrect.
Allow polar bonds do not cancel for PBr3 and polar bonds cancel for SF6.
Do not allow asymmetric molecule as reason for PBr3 or symmetric molecule for SF6 as reason alone.
\(\sigma \) bond:
end-on/axial overlap with electron density between the two carbon atoms/nuclei / end-on/axial overlap of orbitals so shared electrons are between atoms / OWTTE;
\(\pi \) bond:
sideways/parallel overlap of p orbitals with electron density above and below internuclear axis/\(\sigma \) bond / sideways/parallel overlap of p orbitals so shared electrons are above and below internuclear axis/\(\sigma \) bond / OWTTE;
Marks can be scored from a suitable diagram.
Award [1 max] for stating end-on/axial overlap for \(\sigma \) and sideways/parallel overlap for \(\pi \) only i.e. without mentioning electron density OR stating electron density between the two atoms/nuclei for \(\sigma \) and above and below internuclear axis for \(\pi \).
Examiners report
This was usually well answered.
The Lewis structures were usually well drawn but some omitted the lone pairs. The shapes were also usually correct, though some stated that the shape of \({\text{PB}}{{\text{r}}_{\text{3}}}\) is tetrahedral which is incorrect. The electron domain geometry of \({\text{PB}}{{\text{r}}_{\text{3}}}\) is tetrahedral as there are four negative charge centres or four electron domains, but the molecular geometry and hence the shape is trigonal/triangular pyramidal. It is worth emphasising this difference between electron domain geometry and molecular geometry in discussions of shape in VSEPR Theory. As regards the bond angles, a few forgot the fact that the lone pair on the P occupies more space and hence the angle drops below 109.5 degrees. Many simply wrote 107 degrees, which is the bond angle in ammonia. An important point to make here is that every trigonal pyramidal geometry does not have a bond angle equivalent to that of ammonia, 107 degrees, which is a point often misunderstood by candidates. In fact, many factors can come into play here including lone pairs and electronegativity considerations. In fact, the experimental bond angle for \({\text{PB}}{{\text{r}}_{\text{3}}}\) is 101 degrees and candidates would have scored the mark if they gave any value in the range 100 to less than 109.5 degrees. Candidates are not required to know experimental values but should not make sweeping conclusions that all trigonal pyramidal geometries have 107 degree bond angles, which certainly is not the case. For \({\text{S}}{{\text{F}}_{\text{6}}}\), 90 and 120 bond angles were often incorrectly given. The most disappointing part of this sub-section however was the poor explanations of polarity. Some of the top candidates did however give complete explanations and referred to the polar PBr bonds and the fact that as the molecule is not symmetrical there is an asymmetric distribution of the electron cloud. It was nice to see vectorial addition of bond dipoles supporting this type of explanation resulting in a clearly defined and drawn net dipole moment in the case of \({\text{PB}}{{\text{r}}_{\text{3}}}\) leading to its polar nature and similar arguments and drawings in the case of the non-polar of \({\text{S}}{{\text{F}}_{\text{6}}}\).
Very few candidates scored both marks on sigma and pi bonds.

