| Date | May 2017 | Marks available | 5 | Reference code | 17M.1.AHL.TZ1.H_11 |
| Level | Additional Higher Level | Paper | Paper 1 (without calculator) | Time zone | Time zone 1 |
| Command term | Sketch | Question number | H_11 | Adapted from | N/A |
Question
Consider the function .
Express in the form .
Factorize .
Sketch the graph of , indicating on it the equations of the asymptotes, the coordinates of the -intercept and the local maximum.
Hence find the value of if .
Sketch the graph of .
Determine the area of the region enclosed between the graph of , the -axis and the lines with equations and .
Markscheme
A1
[1 mark]
A1
[1 mark]
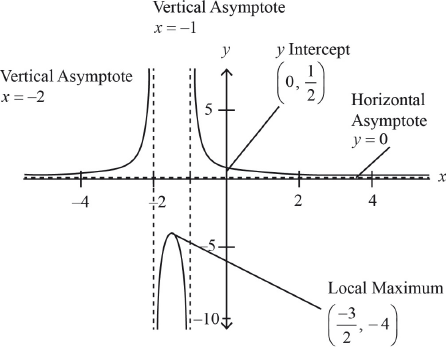
A1 for the shape
A1 for the equation
A1 for asymptotes and
A1 for coordinates
A1 -intercept
[5 marks]
A1
M1
M1A1
[4 marks]
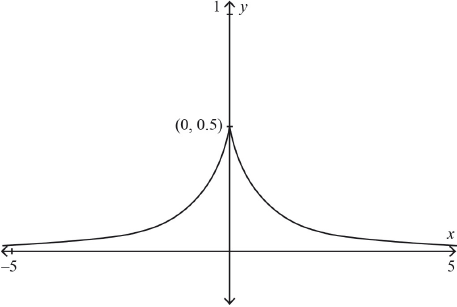
symmetry about the -axis M1
correct shape A1
Note: Allow FT from part (b).
[2 marks]
(M1)(A1)
A1
Note: Do not award FT from part (e).
[3 marks]
Examiners report
Syllabus sections
-
18M.2.SL.TZ1.S_4a:
Write down the coordinates of the vertex of the graph of g.
-
18M.2.SL.TZ2.S_9a:
Find the initial velocity of P.
-
18M.2.SL.TZ2.S_9d:
Find the acceleration of P when it changes direction.
-
19M.1.SL.TZ1.S_7b:
Find the total distance travelled in the first 5 seconds.
-
19M.2.SL.TZ2.S_8c:
Find the value of when particle A first changes direction.
-
22M.1.SL.TZ2.8b:
Find the value of and the value of .
-
17M.1.AHL.TZ1.H_11a.ii:
Factorize .
-
18M.2.SL.TZ1.S_4b:
On the grid above, sketch the graph of g for −2 ≤ x ≤ 4.
-
21N.2.AHL.TZ0.10d:
Sketch the graph of for , clearly indicating the points of intersection with each axis and any asymptotes.
-
16N.2.SL.TZ0.S_9b:
Find the value of .
-
17M.2.SL.TZ1.S_7a.i:
Write down the first value of at which P changes direction.
-
17M.2.SL.TZ1.S_7a.ii:
Find the total distance travelled by P, for .
-
17N.2.SL.TZ0.S_9b:
Hence or otherwise, find all possible values of for which the velocity of P is decreasing.
-
19M.2.AHL.TZ1.H_10a:
Write down the maximum and minimum value of .
-
18M.1.AHL.TZ1.H_4a:
.
-
19M.2.AHL.TZ1.H_10c:
Sketch the graph of for 0 ≤ ≤ 0.02 , showing clearly the coordinates of the first maximum and the first minimum.
-
18M.1.AHL.TZ1.H_7a:
Find .
-
22M.1.AHL.TZ2.8:
A continuous random variable has the probability density function
.
The following diagram shows the graph of for .
Given that , find an expression for the median of in terms of and .
-
18M.2.SL.TZ2.S_9e:
Find the total distance travelled by P.
-
19N.2.SL.TZ0.S_10c:
During the second stage, the rocket accelerates at a constant rate. The distance which the rocket travels during the second stage is the same as the distance it travels during the first stage.
Find the total time taken for the two stages.
-
17M.2.SL.TZ1.S_10b.i:
Find .
-
18N.1.AHL.TZ0.H_10b:
Hence, show that , .
-
21N.1.SL.TZ0.9c.ii:
Find the values of where the graph of has points of inflexion. Justify your answer.
-
19M.1.AHL.TZ2.H_9a:
Find the -coordinates of the points of intersection of the two graphs.
-
17M.1.SL.TZ1.S_10b:
Given that , find .
-
19M.2.SL.TZ2.S_8d:
Find the total distance travelled by particle A in the first 3 seconds.
-
16N.2.SL.TZ0.S_9a:
Find the initial velocity of .
-
19M.2.AHL.TZ1.H_10d:
Find the total time in the interval 0 ≤ ≤ 0.02 for which ≥ 3.
-
17M.2.AHL.TZ1.H_4b:
Calculate the area of .
-
19M.2.AHL.TZ1.H_10g:
Given that can be written as where , , , > 0, use your graph to find the values of , , and .
-
18M.2.SL.TZ2.S_9b:
Find the maximum speed of P.
-
19M.1.SL.TZ2.S_10c:
Write down an expression for the area of .
-
17N.2.SL.TZ0.S_5b:
The following diagram shows part of the graph of .

The region enclosed by the graph of , the -axis and the lines and is rotated 360° about the -axis. Find the volume of the solid formed.
-
17M.1.SL.TZ1.S_10c:
Let , for . The graph of between and is rotated 360° about the -axis. Find the volume of the solid formed.
-
16N.2.SL.TZ0.S_9c:
(i) Find the value of .
(ii) Hence, find the speed of P when .
-
18M.1.SL.TZ1.S_5a:
Find .
-
18N.1.AHL.TZ0.H_10a:
Use integration by parts to show that , .
-
17N.2.SL.TZ0.S_5a:
Find the value of .
-
22M.1.SL.TZ1.2b:
Hence, find the value of .
-
22M.1.SL.TZ1.9b.i:
Show that , where is a positive real constant.
-
22M.1.SL.TZ1.9b.ii:
It is given that , where . Find the value of .
-
18M.1.SL.TZ1.S_5b:
Part of the graph of f is shown in the following diagram.
The shaded region R is enclosed by the graph of f, the x-axis, and the lines x = 1 and x = 9 . Find the volume of the solid formed when R is revolved 360° about the x-axis.
-
19M.2.SL.TZ2.S_8e.i:
Given that particles A and B start at the same point, find the displacement function for particle B.
-
22M.1.AHL.TZ1.12b:
Hence, find an approximate value for .
-
19M.2.AHL.TZ1.H_7:
The function is defined by , ≥ 1 and the function is defined by , ≥ 0.
The region is bounded by the curves , and the lines , and as shown on the following diagram.
The shape of a clay vase can be modelled by rotating the region through 360˚ about the -axis.
Find the volume of clay used to make the vase.
-
22M.1.AHL.TZ2.7:
By using the substitution or otherwise, find an expression for in terms of , where is a non-zero real number.
-
22M.2.SL.TZ1.8c.ii:
Hence, find the area enclosed by the graph of and the graph of .
-
19M.2.AHL.TZ1.H_10b:
Write down two transformations that will transform the graph of onto the graph of .
-
20N.1.AHL.TZ0.H_12b:
State the equation of the horizontal asymptote on the graph of .
-
20N.1.AHL.TZ0.H_12d:
Sketch the graph of , stating clearly the equations of any asymptotes and the coordinates of any points of intersections with the coordinate axes.
-
20N.2.AHL.TZ0.H_3b:
Hence find the area of the shaded region.
-
17N.2.SL.TZ0.S_9a:
Write down the values of when .
-
18M.2.SL.TZ2.S_3a:
Find the x-intercept of the graph of .
-
16N.2.SL.TZ0.S_4b:
Hence, find the area of the region enclosed by the graphs of and .
-
17N.1.SL.TZ0.S_8d:
Find the area of the region enclosed by the graph of and the line .
-
19M.1.SL.TZ2.S_10d:
Hence find the exact area of .
-
19M.2.SL.TZ2.S_8a:
Find the initial displacement of particle A from point P.
-
19M.2.SL.TZ2.S_8e.ii:
Find the other value of when particles A and B meet.
-
20N.2.AHL.TZ0.H_3a:
Determine the values of , and .
-
19M.1.AHL.TZ2.H_9c:
At the points A and B on the diagram, the gradients of the two graphs are equal.
Determine the -coordinate of A on the graph of .
-
19N.2.AHL.TZ0.H_11c:
The region is now rotated about the -axis, through radians, to form a solid.
By writing as , show that the volume of the solid formed is .
-
SPM.1.SL.TZ0.9d:
The region R is enclosed by the graph of , the x-axis, and the vertical lines through the maximum point P and the point of inflexion Q.
Given that the area of R is 3, find the value of .
-
18M.2.SL.TZ2.S_3b:
The region enclosed by the graph of , the y-axis and the x-axis is rotated 360° about the x-axis.
Find the volume of the solid formed.
-
21M.1.SL.TZ2.8b:
Show that the area of the shaded region is .
-
19M.1.AHL.TZ2.H_9b:
Find the exact area of the shaded region, giving your answer in the form , where , .
-
19M.2.SL.TZ2.S_2b:
The region enclosed by the graph of , the -axis and the -axis is rotated 360º about the -axis. Find the volume of the solid formed.
-
SPM.1.SL.TZ0.9b:
Find the x-coordinate of P.
-
18N.1.AHL.TZ0.H_10d:
Find the area enclosed by the curve and the -axis between B and D, as shaded on the diagram.
-
18M.2.SL.TZ2.S_9c:
Write down the number of times that the acceleration of P is 0 m s−2 .
-
18M.1.AHL.TZ2.H_11a:
Show that where .
-
17N.2.SL.TZ0.S_9d:
Find the total distance travelled by P when its velocity is increasing.
-
17M.1.AHL.TZ1.H_11e:
Sketch the graph of .
-
19M.2.AHL.TZ1.H_10e:
Find (0.007).
-
19M.2.SL.TZ2.S_2a:
Find the -intercept of the graph of .
-
17M.2.AHL.TZ1.H_4a:
Write down a definite integral to represent the area of .
-
19M.2.AHL.TZ1.H_10f:
With reference to your graph of explain why > 0 for all > 0.
-
17M.1.AHL.TZ1.H_11d:
Hence find the value of if .
-
EXN.2.SL.TZ0.6b:
Find the area, , of the region enclosed by the two curves.
-
SPM.1.SL.TZ0.9c:
Show that the x-coordinate of Q is .
-
19N.2.SL.TZ0.S_10b:
Find the distance that the rocket travels during the first stage.
-
17M.2.SL.TZ1.S_10a.i:
Write down the value of ;
-
21N.1.SL.TZ0.9a:
Find all the values of where the graph of is increasing. Justify your answer.
-
21N.1.SL.TZ0.9c.i:
Find the value of where the graph of has a local minimum. Justify your answer.
-
21N.1.SL.TZ0.9d:
The total area of the region enclosed by the graph of , the derivative of , and the -axis is .
Given that , find the value of .
-
22M.1.AHL.TZ1.1:
Find the value of .
-
21N.2.AHL.TZ0.10a.ii:
-axis.
-
21N.1.SL.TZ0.9b:
Find the value of where the graph of has a local maximum.
-
21N.2.AHL.TZ0.10c:
The oblique asymptote of the graph of can be written as where .
Find the value of and the value of .
-
19M.2.SL.TZ2.S_8b:
Find the value of when particle A first reaches point P.
-
17N.2.SL.TZ0.S_9c:
Find an expression for the velocity of P at time .
-
17M.1.AHL.TZ1.H_11f:
Determine the area of the region enclosed between the graph of , the -axis and the lines with equations and .
-
19N.1.AHL.TZ0.H_2:
Given that , find the value of .
-
18M.2.SL.TZ1.S_4c:
Find the area of the region enclosed by the graphs of f and g.
-
19N.2.SL.TZ0.S_10a:
Find an expression for the velocity, m s−1, of the rocket during the first stage.
-
17M.2.SL.TZ2.S_7:
Note: In this question, distance is in metres and time is in seconds.
A particle moves along a horizontal line starting at a fixed point A. The velocity of the particle, at time , is given by , for . The following diagram shows the graph of

There are -intercepts at and .
Find the maximum distance of the particle from A during the time and justify your answer.
-
17M.1.SL.TZ1.S_10a:
Show that .
-
18M.1.AHL.TZ1.H_4b:
.
-
20N.1.AHL.TZ0.H_12a:
State the equation of the vertical asymptote on the graph of .
-
20N.1.AHL.TZ0.H_12c:
Use an algebraic method to determine whether is a self-inverse function.
-
19N.1.AHL.TZ0.H_10c:
Show that .
-
19M.1.SL.TZ2.S_10b:
Hence find .
-
SPM.1.SL.TZ0.9a:
Show that .
-
18M.1.AHL.TZ1.H_7b:
Find .
-
17M.1.AHL.TZ1.H_11a.i:
Express in the form .
-
20N.1.AHL.TZ0.H_12e:
The region bounded by the -axis, the curve , and the lines and is rotated through about the -axis. Find the volume of the solid generated, giving your answer in the form , where .
-
17M.2.SL.TZ1.S_7b:
A second particle Q also moves along a straight line. Its velocity, after seconds is given by for . After seconds Q has travelled the same total distance as P.
Find .
-
16N.2.SL.TZ0.S_4a:
Find the value of and of .
-
19N.2.AHL.TZ0.H_11b:
Find the area of .
-
18N.1.AHL.TZ0.H_10c:
Find the -coordinates of A and of C , giving your answers in the form , where , .
-
19N.1.AHL.TZ0.H_10d:
The area enclosed by the graph of and the line can be expressed as . Find the value of .
-
19M.1.SL.TZ1.S_7a:
Find the value of .
-
16N.2.SL.TZ0.S_9d:
(i) Find the total distance travelled by P between and .
(ii) Hence or otherwise, find the displacement of P from A when .
-
18M.1.AHL.TZ2.H_6b:
Hence, or otherwise, find .
-
17M.2.SL.TZ1.S_10a.iii:
Write down the value of .
-
17M.2.SL.TZ1.S_10c:
Let be the vertical distance from a point on the graph of to the line . There is a point on the graph of where is a maximum.
Find the coordinates of P, where .
-
17M.2.SL.TZ1.S_10a.ii:
Write down the value of ;
-
17M.2.SL.TZ1.S_10b.ii:
Hence, find the area of the region enclosed by the graphs of and .
-
21N.2.AHL.TZ0.10e.i:
Express in partial fractions.
-
21N.2.AHL.TZ0.10e.ii:
Hence find the exact value of , expressing your answer as a single logarithm.
-
21N.2.AHL.TZ0.10a.i:
-axis.
-
21N.2.AHL.TZ0.10b:
Write down the equation of the vertical asymptote of the graph of .

