| Date | May 2017 | Marks available | 1 | Reference code | 17M.2.SL.TZ1.S_10 |
| Level | Standard Level | Paper | Paper 2 | Time zone | Time zone 1 |
| Command term | Write down | Question number | S_10 | Adapted from | N/A |
Question
Let and , for .
The graph of can be obtained from the graph of by two transformations:
Let , for . The following diagram shows the graph of and the line .
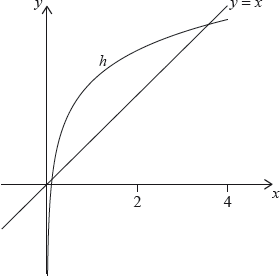
The graph of intersects the graph of at two points. These points have coordinates 0.111 and 3.31 correct to three significant figures.
Write down the value of ;
Write down the value of ;
Write down the value of .
Find .
Hence, find the area of the region enclosed by the graphs of and .
Let be the vertical distance from a point on the graph of to the line . There is a point on the graph of where is a maximum.
Find the coordinates of P, where .
Markscheme
A1 N1
Note: Accept , , and , 2.31 as candidate may have rewritten as equal to .
[1 mark]
A1 N1
Note: Accept , , and , 2.31 as candidate may have rewritten as equal to .
[1 mark]
A1 N1
Note: Accept , , and , 2.31 as candidate may have rewritten as equal to .
[1 mark]
2.72409
2.72 A2 N2
[2 marks]
recognizing area between and equals 2.72 (M1)
eg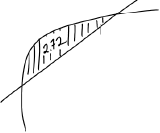
recognizing graphs of and are reflections of each other in (M1)
egarea between and equals between and
5.44819
5.45 A1 N3
[??? marks]
valid attempt to find (M1)
egdifference in -coordinates,
correct expression for (A1)
eg
valid approach to find when is a maximum (M1)
egmax on sketch of , attempt to solve
0.973679
A2 N4
substituting their value into (M1)
2.26938
A1 N2
[7 marks]