Calculate the area of cloth, in cm², needed to make Haruka’s bag.

Write down the $y$-intercept of the graph of $y=f\left(x\right)$.

Find the value of $a$ and the value of $b$.

Solve f '(x) = f "(x).

(i)     Find $h^{\prime }(x)$.

(ii)     Hence, show that $h^{\prime }(\pi )=\frac{-21!}{2}{\pi }^2$.

(i)     Find the first three derivatives of $g(x)$.

(ii)     Given that $g^{(19)}(x)=\frac{k!}{(k-p)!}(x^{k-19})$, find $p$.

Write down the number of possible solutions to the equation $f(x)=5$.

Find $\frac{\text{d}y}{\text{d}x}$.

Sketch the graph of $y=f^{\prime }\left(x\right)$.

Explain why $f$ is an even function.

Sketch the graph of $y=f(x)$ showing clearly the equations of asymptotes and the coordinates of any intercepts with the axes.

(i)     Find the first four derivatives of $f(x)$.

(ii)     Find $f^{(19)}(x)$.

Find $f^{\prime }\left(x\right)$.

Let $\text{C}$ be a point on the graph of $h$. The tangent to the graph of $h$ at $\text{C}$ is parallel to the graph of $f$.

Find the $x$-coordinate of $\text{C}$.

Sketch the graph of $y=f\left(x\right)$ for −3 ≤ $x$ ≤ 3 and −4 ≤ $y$ ≤ 12.

Find $h\left(x\right)$.

Find $f^{\prime }\left(x\right)$.

Find the coordinates of P.

Show that $C=20\pi r^2+\frac{320\pi }{r}$.

Write down an expression for the area of $R$.

The graph of $f$ has a local minimum at the point Q. The line L passes through Q.

Find the value of $a$.

Find $\frac{\text{d}y}{\text{d}x}$ in terms of $x$ and $y$.

Find the values of $d$ for which $g$ is an increasing function.

Hence explain why the graph of $f$ has a local maximum point at $x=a$.

Find the coordinates of the points on the curve $y^3+3x{y}^2-x^3=27$ at which $\frac{\text{d}y}{\text{d}x}=0$.

Write down the gradient of this tangent.

Find $f^{″}\left(b\right)$.

Find the area of the region enclosed by the graph of $f$ and the line $L$.

Calculate $\frac{\text{d}\theta }{\text{d}t}$ when $\theta =\frac{\pi }{3}$.

Hence find the exact area of $R$.

Explain why the inverse function $f^{-1}$ does not exist.

Hence, show that there are no solutions to $g^{\prime }(x)=0$;

The folium of Descartes is a curve defined by the equation $x^3+y^3-3xy=0$, shown in the following diagram.

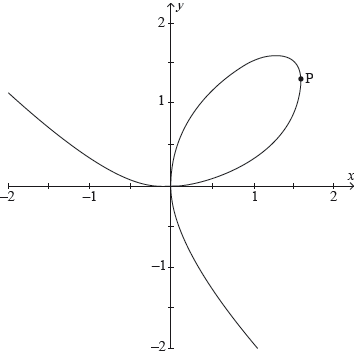
Determine the exact coordinates of the point P on the curve where the tangent line is parallel to the $y$-axis.

Find $f^{\prime }(x)$.

Find the largest possible domain $D$ for $f$ to be a function.

Find the area of triangle $\text{AOB}$ in terms of $k$.

Write down an expression for $f\text{'}\left(x\right)$.

Consider f(x), g(x) and h(x), for x∈$\mathbb{R}$ where h(x) = $\left(f\circ g\right)$(x).

Given that g(3) = 7 , g′ (3) = 4 and f ′ (7) = −5 , find the gradient of the normal to the curve of h at x = 3.

Let $f(x)=(x^2+3{)}^7$. Find the term in $x^5$ in the expansion of the derivative, $f^{\prime }(x)$.

Find $g^{\prime }(x)$.

Express h in terms of r.

The graph of $f$ is translated by $\left(\begin{array}{c}4\\ 3\end{array}\right)$ to give the graph of $g$.
In the following diagram:

• point $\text{Q}$ lies on the graph of $g$
• points $\text{C}$, $\text{D}$ and $\text{E}$ lie on the vertical asymptote of $g$
• points $\text{D}$ and $\text{F}$ lie on the horizontal asymptote of $g$
• point $\text{G}$ lies on the $x$-axis such that $\text{FG}$ is parallel to $\text{DC}$.

Line $L_2$ is the tangent to the graph of $g$ at $\text{Q}$, and passes through $\text{E}$ and $\text{F}$.

Given that triangle $\text{EDF}$ and rectangle $\text{CDFG}$ have equal areas, find the gradient of $L_2$ in terms of $p$.

Hence, find the number of vases that will maximize the profit.

Find the inverse function $g^{-1}$ and state its domain.

Show that the equation of $L_1$ is $kx+p^{2}y-2pk=0$.

The normal to the graph of $f$ at $x=a$ and the tangent to the graph of $f$ at $x=b$ intersect at the point ($p$, $q$) .

Find the value of $p$ and the value of $q$.

Find $f\text{'}\left(p\right)$ in terms of $k$ and $p$.

Write down an equation for the area, $A$, of the curved surface in terms of $r$.

Find the value of $P$ if no vases are sold.

Write down the $x$-coordinates of these two points;

Expand the expression for $f(x)$.

The line $y=kx-5$ is a tangent to the curve of $f$. Find the values of $k$.

Express this volume in $\text{c}{\text{m}}^3$.

Write down, in terms of $r$ and $h$, an equation for the volume of this water container.

Find $\frac{\text{d}A}{\text{d}r}$.

Using your answer to part (e), find the value of $r$ which minimizes $A$.

Find an expression for the volume of water $V({\text{m}}^3)$ in the trough in terms of $\theta$.

Hence, find the equation of L in terms of $a$.

Given that there is a minimum value for C, find this minimum value in terms of $\pi$.

An earth satellite moves in a path that can be described by the curve $72.5x^2+71.5y^2=1$ where $x=x(t)$ and $y=y(t)$ are in thousands of kilometres and $t$ is time in seconds.

Given that $\frac{\text{d}x}{\text{d}t}=7.75\times {10}^{-5}$ when $x=3.2\times {10}^{-3}$, find the possible values of $\frac{\text{d}y}{\text{d}t}$.

Give your answers in standard form.

Hence, use your answer to part (d)(i) to show that the graph of $f$ has a local minimum point at $x=b$.

Determine the equation of the tangent to $C$ at the point $\left(\frac{2}{\text{e}},\text{ e}\right)$

Hence find $\int \left(3x^2+1\right)\sqrt{x^3+x}\text{d}x$.

Find ${\int }_0^1\text{arccos}\left(\frac{x}{2}\right)\text{d}x$.

Hence, show that there are no solutions to $(g^{-1}{)}^{\prime }(x)=0$.

Find $\frac{\text{d}y}{\text{d}x}$.

Use your answer to part (f) to show that the width of Nanako’s bag is 12 cm.

Find the value of $r$ when the area of the curved surface is maximized.

Write down and simplify an expression in x and y for the area of cloth, A, used to make Nanako’s bag.

Differentiate $P\left(x\right)$.

Find the value of $k$.

Write down the $y$-intercept of the graph.

Show that $a=8$.

Find $f^{\prime }(x)$.

Write down $f\prime \left(x\right)$.

Determine the range of $f\left(x\right)$ for $p$ ≤ $x$ ≤ $q$.

Write down the coordinates of the point of intersection.

The equation $f(x)=m$, where $m\in \mathbb{R}$, has four solutions. Find the possible values of $m$.

Show that $A=\pi r^2+\frac{1000000}{r}$.

Find the value of this minimum area.

Find $\frac{\text{d}A}{\text{d}r}$.

Use your answers to parts (c) and (d) to show that

$A=3x^2+\frac{10368}{x}$.

Write down a formula for $A$, the surface area to be coated.

Find the least number of cans of water-resistant material that will coat the area in part (g).

Draw the graph of $f$ for $-3⩽x⩽3$ and $-40⩽y⩽20$. Use a scale of 2 cm to represent 1 unit on the $x$-axis and 1 cm to represent 5 units on the $y$-axis.

Find $f(2)$.

Write down the intervals where the gradient of the graph of $y=f(x)$ is positive.

Write down the range of $f(x)$.

Calculate the volume, in cm³, of the bag.

Use this value to write down, and simplify, the equation in x and y for the volume of Nanako’s bag.

Find $\frac{\text{d}A}{\text{d}x}$.