| Date | May 2013 | Marks available | 3 | Reference code | 13M.2.sl.TZ2.3 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find | Question number | 3 | Adapted from | N/A |
Question
The following diagram shows a triangle ABC.
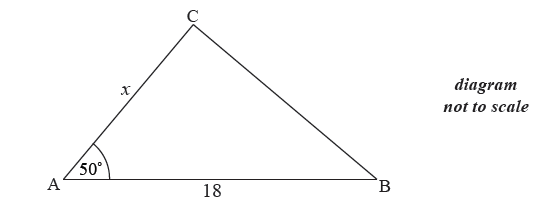
The area of triangle ABC is \(80\) cm2 , AB \( = 18\) cm , AC \( = x\) cm and \({\rm{B}}\hat {\rm{A}}{\rm{C}} = {50^ \circ }\) .
Find \(x\) .
Find BC.
Markscheme
correct substitution into area formula (A1)
eg \(\frac{1}{2}(18x)\sin 50\)
setting their area expression equal to \(80\) (M1)
eg \(9x\sin 50 = 80\)
\(x = 11.6\) A1 N2
[3 marks]
evidence of choosing cosine rule (M1)
eg \({c^2} = {a^2} + {b^2} + 2ab\sin C\)
correct substitution into right hand side (may be in terms of \(x\)) (A1)
eg \({11.6^2} + {18^2} - 2(11.6)(18)\cos 50\)
BC \( = 13.8\) A1 N2
[3 marks]
Examiners report
The vast majority of candidates were very successful with this question. A small minority drew an altitude from C and used right triangle trigonometry. Errors included working in radian mode, assuming that the angle at C was \(90^\circ \), and incorrectly applying the order of operations when evaluating the cosine rule.
The vast majority of candidates were very successful with this question. A small minority drew an altitude from C and used right triangle trigonometry. Errors included working in radian mode, assuming that the angle at C was \(90^\circ \), and incorrectly applying the order of operations when evaluating the cosine rule.

