| Date | May 2008 | Marks available | 3 | Reference code | 08M.2.sl.TZ1.2 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Find | Question number | 2 | Adapted from | N/A |
Question
The diagram below shows triangle PQR. The length of [PQ] is 7 cm , the length of [PR] is 10 cm , and \({\rm{P}}\widehat {\rm{Q}}{\rm{R}}\) is \(75^\circ \) .
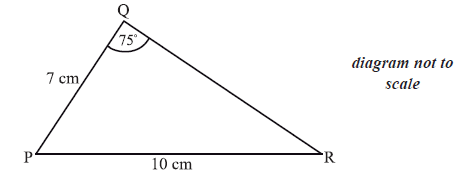
Find \({\rm{P}}\widehat {\rm{R}}{\rm{Q}}\) .
Find the area of triangle PQR.
Markscheme
choosing sine rule (M1)
correct substitution \(\frac{{\sin R}}{7} = \frac{{\sin 75^\circ }}{{10}}\) A1
\(\sin R = 0.676148 \ldots \)
\({\rm{P}}\widehat {\rm{R}}{\rm{Q = 42}}{\rm{.5}}^\circ \) A1 N2
[3 marks]
\(P = 180 - 75 - R\)
\(P = 62.5\) (A1)
substitution into any correct formula A1
e.g. \({\text{area }}\Delta {\text{PQR}} = \frac{1}{2} \times 7 \times 10 \times \sin ({\text{their }}P)\)
\(= 31.0\) (cm2) A1 N2
[3 marks]
Examiners report
This question was well done with most students using the law of sines to find the angle.
In part (b), the most common error occurred when angle R or 75 degrees was used to find the area. This particular question was the most common place to incur an accuracy penalty.

