| Date | May 2013 | Marks available | 4 | Reference code | 13M.2.sl.TZ1.8 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Hence or otherwise | Question number | 8 | Adapted from | N/A |
Question
The diagram shows a circle of radius \(8\) metres. The points ABCD lie on the circumference of the circle.
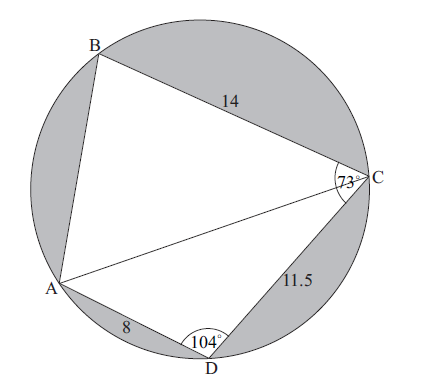
BC = \(14\) m, CD = \(11.5\) m, AD = \(8\) m, \(A\hat DC = {104^ \circ }\) , and \(B\hat CD = {73^ \circ }\) .
Find AC.
(i) Find \(A\hat CD\) .
(ii) Hence, find \(A\hat CB\) .
Find the area of triangle ADC.
(c) Find the area of triangle ADC.
(d) Hence or otherwise, find the total area of the shaded regions.
Hence or otherwise, find the total area of the shaded regions.
Markscheme
evidence of choosing cosine rule (M1)
eg \({c^2} = {a^2} + {b^2} - 2ab\cos C\) , \({\rm{C}}{{\rm{D}}^2} + {\rm{A}}{{\rm{D}}^2} - 2 \times {\rm{CD}} \times {\rm{AD}}\cos D\)
correct substitution A1
eg \({11.5^2} + {8^2} - 2 \times 11.5 \times 8\cos 104\) , \(196.25 - 184\cos 104\)
AC \( = 15.5\) (m) A1 N2
[3 marks]
(i) METHOD 1
evidence of choosing sine rule (M1)
eg \(\frac{{\sin A}}{a} = \frac{{\sin B}}{b}\) , \(\frac{{\sin {\rm{A}}\widehat {\rm{C}}{\rm{D}}}}{{{\rm{AD}}}} = \frac{{\sin D}}{{{\rm{AC}}}}\)
correct substitution A1
eg \(\frac{{\sin {\rm{A}}\hat {\rm{C}}{\rm{D}}}}{8} = \frac{{\sin 104}}{{15.516 \ldots }}\)
\({\rm{A}}\hat {\rm{C}}{\rm{D}} = {30.0^ \circ }\) A1 N2
METHOD 2
evidence of choosing cosine rule (M1)
eg \({c^2} = {a^2} + {b^2} - 2ab\cos C\)
correct substitution A1
e.g. \({8^2} = {11.5^2} + 15.516{ \ldots ^2} - 2(11.5)(15.516 \ldots )\cos C\)
\({\rm{A}}\hat {\rm{C}}{\rm{D}} = {30.0^ \circ }\) A1 N2
(ii) subtracting their \({\rm{A}}\hat {\rm{C}}{\rm{D}}\) from \(73\) (M1)
eg \({\rm{7}}3 - {\rm{A}}\hat {\rm{C}}{\rm{D}}\) , \(70 - 30.017 \ldots \)
\({\rm{A}}\hat {\rm{C}}{\rm{B}} = {43.0^ \circ }\) A1 N2
[5 marks]
correct substitution (A1)
eg area \(\Delta {\rm{ADC}} = \frac{1}{2}(8)(11.5)\sin 104\)
area \( = 44.6\) (m2) A1 N2
[2 marks]
(c) correct substitution (A1)
eg area \(\Delta {\rm{ADC}} = \frac{1}{2}(8)(11.5)\sin 104\)
area \( = 44.6\) (m2) A1 N2
[2 marks]
(d) attempt to subtract (M1)
eg \({\rm{circle}} - {\rm{ABCD}}\) , \(\pi {r^2} - \Delta {\rm{ADC}} - \Delta {\rm{ACB}}\)
area \(\Delta {\rm{ACB = }}\frac{1}{2}(15.516 \ldots )(14)\sin 42.98\) (A1)
correct working A1
eg \(\pi {(8)^2} - 44.6336 \ldots - \frac{1}{2}(15.516 \ldots )(14)\sin 42.98\) , \(64\pi - 44.6 - 74.1\)
shaded area is \(82.4\) (m2) A1 N3
[4 marks]
Total [6 marks]
attempt to subtract (M1)
eg \({\rm{circle}} - {\rm{ABCD}}\) , \(\pi {r^2} - \Delta {\rm{ADC}} - \Delta {\rm{ACB}}\)
area \(\Delta {\rm{ACB = }}\frac{1}{2}(15.516 \ldots )(14)\sin 42.98\) (A1)
correct working A1
eg \(\pi {(8)^2} - 44.6336 \ldots - \frac{1}{2}(15.516 \ldots )(14)\sin 42.98\) , \(64\pi - 44.6 - 74.1\)
shaded area is \(82.4\) (m2) A1 N3
[4 marks]
Total [6 marks]
Examiners report
There was an error on this question, where the measurements were inconsistent. Whichever method a candidate used to answer the question, the inconsistencies did not cause a problem. The markscheme included a variety of solutions based on possible combinations of solutions, and examiners were instructed to notify the IB assessment centre of any candidates adversely affected. Candidate scripts did not indicate any adverse effect.
Despite this unfortunate error, the question posed few difficulties for candidates and most approached the problem as intended. Although there were other ways to approach the problem (using properties of cyclic quadrilaterals) few considered this, likely due to the fact that cyclic quadrilaterals is not part of the syllabus.
There was an error on this question, where the measurements were inconsistent. Whichever method a candidate used to answer the question, the inconsistencies did not cause a problem. The markscheme included a variety of solutions based on possible combinations of solutions, and examiners were instructed to notify the IB assessment centre of any candidates adversely affected. Candidate scripts did not indicate any adverse effect.
Despite this unfortunate error, the question posed few difficulties for candidates and most approached the problem as intended. Although there were other ways to approach the problem (using properties of cyclic quadrilaterals) few considered this, likely due to the fact that cyclic quadrilaterals is not part of the syllabus.
There was an error on this question, where the measurements were inconsistent. Whichever method a candidate used to answer the question, the inconsistencies did not cause a problem. The markscheme included a variety of solutions based on possible combinations of solutions, and examiners were instructed to notify the IB assessment centre of any candidates adversely affected. Candidate scripts did not indicate any adverse effect.
Despite this unfortunate error, the question posed few difficulties for candidates and most approached the problem as intended. Although there were other ways to approach the problem (using properties of cyclic quadrilaterals) few considered this, likely due to the fact that cyclic quadrilaterals is not part of the syllabus. Candidates were proficient in their use of sine and cosine rules and most could find the area of the required triangle in part (c). Those who made errors in this question either had their GDC in the wrong mode or were rounding values prematurely while some misinformed candidates treated ADC as a right-angled triangle.
There was an error on this question, where the measurements were inconsistent. Whichever method a candidate used to answer the question, the inconsistencies did not cause a problem. The markscheme included a variety of solutions based on possible combinations of solutions, and examiners were instructed to notify the IB assessment centre of any candidates adversely affected. Candidate scripts did not indicate any adverse effect.
Despite this unfortunate error, the question posed few difficulties for candidates and most approached the problem as intended. Although there were other ways to approach the problem (using properties of cyclic quadrilaterals) few considered this, likely due to the fact that cyclic quadrilaterals is not part of the syllabus. Candidates were proficient in their use of sine and cosine rules and most could find the area of the required triangle in part (c). Those who made errors in this question either had their GDC in the wrong mode or were rounding values prematurely while some misinformed candidates treated ADC as a right-angled triangle. In part (d), most candidates recognized what to do and often obtained follow through marks from errors made in previous parts.
There was an error on this question, where the measurements were inconsistent. Whichever method a candidate used to answer the question, the inconsistencies did not cause a problem. The markscheme included a variety of solutions based on possible combinations of solutions, and examiners were instructed to notify the IB assessment centre of any candidates adversely affected. Candidate scripts did not indicate any adverse effect.
Despite this unfortunate error, the question posed few difficulties for candidates and most approached the problem as intended. Although there were other ways to approach the problem (using properties of cyclic quadrilaterals) few considered this, likely due to the fact that cyclic quadrilaterals is not part of the syllabus.
In part (d), most candidates recognized what to do and often obtained follow through marks from errors made in previous parts.

