| Date | May 2016 | Marks available | 5 | Reference code | 16M.1.sl.TZ2.5 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find | Question number | 5 | Adapted from | N/A |
Question
The following diagram shows a triangle ABC and a sector BDC of a circle with centre B and radius 6 cm. The points A , B and D are on the same line.
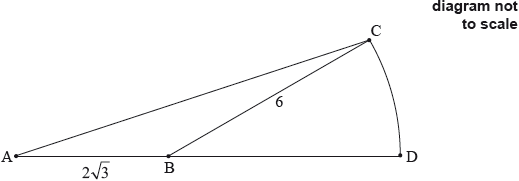
\({\text{AB}} = 2\sqrt 3 {\text{ cm, BC}} = 6{\text{ cm, area of triangle ABC}} = 3\sqrt 3{\text{ c}}{{\text{m}}^{\text{2}}}{\rm{, A\hat BC}}\) is obtuse.
Find \({\rm{A\hat BC}}\).
Find the exact area of the sector BDC.
Markscheme
METHOD 1
correct substitution into formula for area of triangle (A1)
eg\(\,\,\,\,\,\)\(\frac{1}{2}(6)\left( {2\sqrt 3 } \right)\sin B,{\text{ }}6\sqrt 3 \sin B,{\text{ }}\frac{1}{2}(6)\left( {2\sqrt 3 } \right)\sin B = 3\sqrt 3 \)
correct working (A1)
eg\(\,\,\,\,\,\)\(6\sqrt 3 \sin B = 3\sqrt 3 ,{\text{ }}\sin B = \frac{{3\sqrt 3 }}{{\frac{1}{2}(6)2\sqrt 3 }}\)
\(\sin B = \frac{1}{2}\) (A1)
\(\frac{\pi }{6}(30^\circ )\) (A1)
\({\rm{A\hat BC}} = \frac{{5\pi }}{6}(150^\circ )\) A1 N3
METHOD 2
(using height of triangle ABC by drawing perpendicular segment from C to AD)
correct substitution into formula for area of triangle (A1)
eg\(\,\,\,\,\,\)\(\frac{1}{2}\left( {2\sqrt 3 } \right)(h) = 3\sqrt 3 ,{\text{ }}h\sqrt 3 \)
correct working (A1)
eg\(\,\,\,\,\,\)\(h\sqrt 3 = 3\sqrt 3 \)
height of triangle is 3 A1
\({\rm{C\hat BD}} = \frac{\pi }{6}(30^\circ )\) (A1)
\({\rm{A\hat BC}} = \frac{{5\pi }}{6}(150^\circ )\) A1 N3
[5 marks]
recognizing supplementary angle (M1)
eg\(\,\,\,\,\,\)\({\rm{C\hat BD}} = \frac{\pi }{6},{\text{ sector}} = \frac{1}{2}(180 - {\rm{A\hat BC)(}}{{\text{6}}^2})\)
correct substitution into formula for area of sector (A1)
eg\(\,\,\,\,\,\)\(\frac{1}{2} \times \frac{\pi }{6} \times {6^2},{\text{ }}\pi ({6^2})\left( {\frac{{30}}{{360}}} \right)\)
\({\text{area}} = 3\pi {\text{ }}({\text{c}}{{\text{m}}^2})\) A1 N2
[3 marks]
Examiners report
In part (a) of this question, the large majority of candidates substituted correctly into the area formula for the triangle, though algebraic errors kept some of them from simplifying the equation to \(\sin {\rm{A\hat BC = }}\frac{1}{2}\). Unfortunately, a number of candidates who got to this point often did not know the correct angles that correspond with this sine value.
In part (b), many candidates realized that \({\rm{C\hat BD}}\) was the supplement of \({\rm{A\hat BC}}\). However, at this point many candidates substituted 30°, or their follow-through angle in degrees, into the formula for the area of a sector found in the formula booklet, not understanding that this formula only works for angles in radians.

