| Date | May 2012 | Marks available | 2 | Reference code | 12M.2.sl.TZ2.1 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find | Question number | 1 | Adapted from | N/A |
Question
The following diagram shows \(\Delta {\rm{PQR}}\) , where RQ = 9 cm, \({\rm{P\hat RQ}} = {70^ \circ }\) and \({\rm{P\hat QR}} = {45^ \circ }\) .
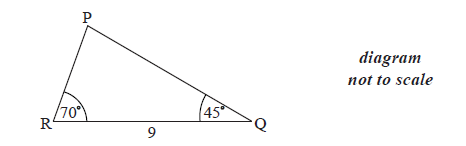
Find \({\rm{R\hat PQ}}\) .
Find PR .
Find the area of \(\Delta {\rm{PQR}}\) .
Markscheme
\({\rm{R\hat PQ = }}{65^ \circ }\) A1 N1
[1 mark]
evidence of choosing sine rule (M1)
correct substitution A1
e.g. \(\frac{{{\rm{PR}}}}{{\sin {{45}^ \circ }}} = \frac{9}{{\sin {{65}^ \circ }}}\)
7.021854078
\({\rm{PR}} = 7.02\) A1 N2
[3 marks]
correct substitution (A1)
e.g. \({\rm{area}} = \frac{1}{2} \times 9 \times 7.02 \ldots \times \sin {70^ \circ }\)
\(29.69273008\)
\({\rm{area}} = 29.7\) A1 N2
[2 marks]
Examiners report
This question was attempted in a satisfactory manner.
The sine rule was applied satisfactory in part (b) but some obtained an incorrect answer due to having their calculators in radian mode. Some incorrect substitutions were seen, either by choosing an incorrect side or substituting 70 instead of \(\sin {70^ \circ }\) . Approaches using a combination of the cosine rule and/or right-angled triangle trigonometry were seen.
Approaches using a combination of the cosine rule and/or right-angled triangle trigonometry were seen, especially in part (c) to calculate the area of the triangle.
A few candidates set about finding the height, then used the formula for the area of a right-angled triangle.

