| Date | November 2016 | Marks available | 2 | Reference code | 16N.1.sl.TZ0.8 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Write down | Question number | 8 | Adapted from | N/A |
Question
Let \(\overrightarrow {{\text{OA}}} = \left( {\begin{array}{*{20}{c}} { - 1} \\ 0 \\ 4 \end{array}} \right)\) and \(\overrightarrow {{\text{OB}}} = \left( {\begin{array}{*{20}{c}} 4 \\ 1 \\ 3 \end{array}} \right)\).
The point C is such that \(\overrightarrow {{\text{AC}}} = \left( {\begin{array}{*{20}{c}} { - 1} \\ 1 \\ { - 1} \end{array}} \right)\).
The following diagram shows triangle ABC. Let D be a point on [BC], with acute angle \({\text{ADC}} = \theta \).
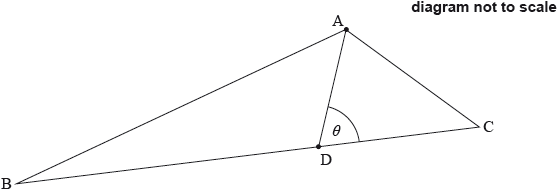
(i) Find \(\overrightarrow {{\text{AB}}} \).
(ii) Find \(\left| {\overrightarrow {{\text{AB}}} } \right|\).
Show that the coordinates of C are \(( - 2,{\text{ }}1,{\text{ }}3)\).
Write down an expression in terms of \(\theta \) for
(i) angle ADB;
(ii) area of triangle ABD.
Given that \(\frac{{{\text{area }}\Delta {\text{ABD}}}}{{{\text{area }}\Delta {\text{ACD}}}} = 3\), show that \(\frac{{{\text{BD}}}}{{{\text{BC}}}} = \frac{3}{4}\).
Hence or otherwise, find the coordinates of point D.
Markscheme
(i) valid approach to find \(\overrightarrow {{\text{AB}}} \)
eg\(\,\,\,\,\,\)\(\overrightarrow {{\text{OB}}} - \overrightarrow {{\text{OA}}} ,{\text{ }}\left( {\begin{array}{*{20}{c}} {4 - ( - 1)} \\ {1 - 0} \\ {3 - 4} \end{array}} \right)\)
\(\overrightarrow {{\text{AB}}} = \left( {\begin{array}{*{20}{c}} 5 \\ 1 \\ { - 1} \end{array}} \right)\) A1 N2
(ii) valid approach to find \(\left| {\overrightarrow {{\text{AB}}} } \right|\) (M1)
eg\(\,\,\,\,\,\)\(\sqrt {{{(5)}^2} + {{(1)}^2} + {{( - 1)}^2}} \)
\(\left| {\overrightarrow {{\text{AB}}} } \right| = \sqrt {27} \) A1 N2
[4 marks]
correct approach A1
eg\(\,\,\,\,\,\)\(\overrightarrow {{\text{OC}}} = \left( {\begin{array}{*{20}{c}} { - 1} \\ 1 \\ { - 1} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} { - 1} \\ 0 \\ 4 \end{array}} \right)\)
\(C\) has coordinates \(( - 2,{\text{ }}1,{\text{ }}3)\) AG N0
[1 mark]
(i) \({\rm{A\hat DB}} = \pi - \theta ,{\rm{ \hat D}} = 180 - \theta \) A1 N1
(ii) any correct expression for the area involving \(\theta \) A1 N1
eg\(\,\,\,\,\,\)\({\text{area}} = \frac{1}{2} \times {\text{AD}} \times {\text{BD}} \times \sin (180 - \theta ),{\text{ }}\frac{1}{2}ab\sin \theta ,{\text{ }}\frac{1}{2}\left| {\overrightarrow {{\text{DA}}} } \right|\left| {\overrightarrow {{\text{DB}}} } \right|\sin (\pi - \theta )\)
[2 marks]
METHOD 1 (using sine formula for area)
correct expression for the area of triangle ACD (seen anywhere) (A1)
eg\(\,\,\,\,\,\)\(\frac{1}{2}{\text{AD}} \times {\text{DC}} \times \sin \theta \)
correct equation involving areas A1
eg\(\,\,\,\,\,\)\(\frac{{\frac{1}{2}{\text{AD}} \times {\text{BD}} \times \sin (\pi - \theta )}}{{\frac{1}{2}{\text{AD}} \times {\text{DC}} \times \sin \theta }} = 3\)
recognizing that \(\sin (\pi - \theta ) = \sin \theta \) (seen anywhere) (A1)
\(\frac{{{\text{BD}}}}{{{\text{DC}}}} = 3\) (seen anywhere) (A1)
correct approach using ratio A1
eg\(\,\,\,\,\,\)\(3\overrightarrow {{\text{DC}}} + \overrightarrow {{\text{DC}}} = \overrightarrow {{\text{BC}}} ,{\text{ }}\overrightarrow {{\text{BC}}} = 4\overrightarrow {{\text{DC}}} \)
correct ratio \(\frac{{{\text{BD}}}}{{{\text{BC}}}} = \frac{3}{4}\) AG N0
METHOD 2 (Geometric approach)
recognising \(\Delta {\text{ABD}}\) and \(\Delta {\text{ACD}}\) have same height (A1)
eg\(\,\,\,\,\,\)use of \(h\) for both triangles, \(\frac{{\frac{1}{2}{\text{BD}} \times h}}{{\frac{1}{2}{\text{CD}} \times h}} = 3\)
correct approach A2
eg\(\,\,\,\,\,\)\({\text{BD}} = 3x\) and \({\text{DC}} = x,{\text{ }}\frac{{{\text{BD}}}}{{{\text{DC}}}} = 3\)
correct working A2
eg\(\,\,\,\,\,\)\({\text{BC}} = 4x,{\text{ BD}} + {\text{DC}} = 4{\text{DC, }}\frac{{{\text{BD}}}}{{{\text{BC}}}} = \frac{{3x}}{{4x}},{\text{ }}\frac{{{\text{BD}}}}{{{\text{BC}}}} = \frac{{3{\text{DC}}}}{{4{\text{DC}}}}\)
\(\frac{{{\text{BD}}}}{{{\text{BC}}}} = \frac{3}{4}\) AG N0
[5 marks]
correct working (seen anywhere) (A1)
eg\(\,\,\,\,\,\)\(\overrightarrow {{\text{BD}}} = \frac{3}{4}\overrightarrow {{\text{BC}}} ,{\text{ }}\overrightarrow {{\text{OD}}} = \overrightarrow {{\text{OB}}} + \frac{3}{4}\left( {\begin{array}{*{20}{c}} { - 6} \\ 0 \\ 0 \end{array}} \right),{\text{ }}\overrightarrow {{\text{CD}}} = \frac{1}{4}\overrightarrow {{\text{CB}}} \)
valid approach (seen anywhere) (M1)
eg\(\,\,\,\,\,\)\(\overrightarrow {{\text{OD}}} = \overrightarrow {{\text{OB}}} + \overrightarrow {{\text{BD}}} ,{\text{ }}\overrightarrow {{\text{BC}}} = \left( {\begin{array}{*{20}{c}} { - 6} \\ 0 \\ 0 \end{array}} \right)\)
correct working to find \(x\)-coordinate (A1)
eg\(\,\,\,\,\,\)\(\left( {\begin{array}{*{20}{c}} 4 \\ 1 \\ 3 \end{array}} \right) + \frac{3}{4}\left( {\begin{array}{*{20}{c}} { - 6} \\ 0 \\ 0 \end{array}} \right),{\text{ }}x = 4 + \frac{3}{4}( - 6),{\text{ }} - 2 + \frac{1}{4}(6)\)
D is \(\left( { - \frac{1}{2},{\text{ }}1,{\text{ }}3} \right)\) A1 N3
[4 marks]

