| Date | November 2017 | Marks available | 3 | Reference code | 17N.2.sl.TZ0.1 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 1 | Adapted from | N/A |
Question
The following diagram shows a triangle ABC.
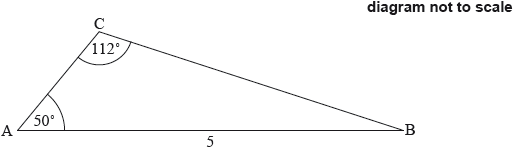
\({\text{AB}} = 5{\rm{ cm, C\hat AB}} = \) 50° and \({\rm{A\hat CB}} = \) 112°
Find BC.
Find the area of triangle ABC.
Markscheme
evidence of choosing sine rule (M1)
eg\(\,\,\,\,\,\)\(\frac{{\sin A}}{a} = \frac{{\sin B}}{b}\)
correct substitution (A1)
eg\(\,\,\,\,\,\)\(\frac{{{\text{BC}}}}{{\sin 50}} = \frac{5}{{\sin 112}}\)
4.13102
\({\text{BC}} = 4.13{\text{ (cm)}}\) A1 N2
[3 marks]
correct working (A1)
eg\(\,\,\,\,\,\)\({\rm{\hat B}} = 180 - 50 - 112\), 18°, \({\text{AC}} = 1.66642\)
correct substitution into area formula (A1)
eg\(\,\,\,\,\,\)\(\frac{1}{2} \times 5 \times 4.13 \times \sin 18,{\text{ }}0.5(5)(1.66642)\sin 50,{\text{ }}\frac{1}{2}(4.13)(1.66642)\sin 112\)
3.19139
\({\text{area}} = 3.19{\text{ (c}}{{\text{m}}^2}{\text{)}}\) A1 N2
[3 marks]

