| Date | May 2015 | Marks available | 3 | Reference code | 15M.2.sl.TZ2.1 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find | Question number | 1 | Adapted from | N/A |
Question
The following diagram shows triangle \(ABC\).
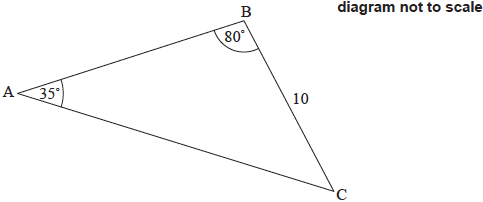
\[{\text{BC}} = 10{\text{ cm}},{\rm{ A\hat BC}} = 80^\circ \;{\text{and}}\;{\rm{B\hat AC}} = 35^\circ .\]
Find \(AC\).
Find the area of triangle \(ABC\).
Markscheme
evidence of choosing sine rule (M1)
eg\(\;\;\;\frac{{{\text{AC}}}}{{\sin ({\rm{A\hat BC)}}}} = \frac{{{\text{BC}}}}{{\sin ({\rm{B\hat AC)}}}}\)
correct substitution (A1)
eg\(\;\;\;\frac{{{\text{AC}}}}{{\sin 80^\circ }} = \frac{{10}}{{\sin 35^\circ }}\)
\({\text{AC}} = 17.1695\)
\({\text{AC}} = 17.2{\text{ (cm)}}\) A1 N2
[3 marks]
\({\rm{A\hat CB}} = 65^\circ \;\;\;\)(seen anywhere) (A1)
correct substitution (A1)
eg\(\;\;\;\frac{1}{2} \times 10 \times 17.1695 \times \sin 65^\circ \)
\({\text{area}} = 77.8047\)
\({\text{area}} = 77.8{\text{ (c}}{{\text{m}}^{\text{2}}}{\text{)}}\) A1 N2
[3 marks]
Total [6 marks]
Examiners report
Most candidates found this question straightforward and accessible.
Most recognized the need for the sine rule in part (a) to solve the problem. Occasionally, the setup had an incorrect match of angle and side. Some used radians instead of degrees, thus losing a mark.
Part (b) was also well done by most of the candidates. Some right triangle trigonometry correct approaches were seen to find the area. A few candidates used the cosine rule or right angled trigonometry, which were less efficient methods and often wasted valuable time.

