Home
 

Practice Questions

  1. Home
  2. Practice Questions

This page is a place where all the quizzes from the different chapters are written in one place. Please don't forget to go back to all of the individual pages for help in between if and when you need it! Remember, that whilst practising questions is an excellent way to revise, you will then have to do something about what you weren't able to do the first time, by going back to your resources for revision.

Number and Algebra

Exponents

1

Find

\({ 5 }^{ -2 }\times { 5 }^{ 5 }\)

When the bases are the same, multiply the exponents only.

\({ =5 }^{ (-2+5) }\)

2

Simplify

\({ { (2 }^{ 3 }) }^{ 4 }\)

This is equivalent to \({ { 2 }^{ 3 } } \times { { 2 }^{ 3 } } \times{ { 2 }^{ 3 } } \times { { 2 }^{ 3 } } .\) As the bases are the same we can now simply add together the exponents.

3

Simplify

\(3{ y }^{ -2 } \)

\(3{ y }^{ -2 }=3{ \quad \times \quad y }^{ -2 }\)

\({ y }^{ -2 }=\frac { 1 }{ y^2 } \)

Therefore

\({ 3y }^{ -2 }=3\times \frac { 1 }{ y^2 } \)

4

If \({ a }^{ 3 }\times { a }^{ 4 }={ a }^{ n }\), what is \(n\)?

n =

\({ a }^{ m }\times { a }^{ n }={ a }^{ m+n }\)

5

If \({ ({ 2p }^{ 3 }) }^{ 2 }=a{ p }^{ n }\), what are the values of \(a\) and \(n\)?

a =

n =

\({ ({ 2p }^{ 3 }) }^{ 2 }={ 2 }^{ 2 }\times { p }^{ 3\times 2 }=4{ p }^{ 6 }\)

6

If \({ 5 }^{ -1 } =n\), what is the value of \(n\)? (Without a calculator)

n =

\({ 5 }^{ -1 }=\frac { 1 }{ { 5 } } =0.2\)
7

If \({ ({ 3 }^{ 0 }) }^{ -3 }=\frac { m }{ n } \), what are the values of \(m\) and \(n\)? (Without a calculator)

m =

n =

\({ ({ 3 }^{ 0 }) }^{ -3 }={ 1 }^{ -3 }=\frac { 1 }{ { 1 }^{ 3 } } =\frac { 1 }{ 1 } \)
8

If \({ (\frac { { 9x }^{ 5 } }{ { 4y }^{ 7 } } ) }^{ -3 }=\frac { a{ y }^{ b } }{ m{ x }^{ n } } \), what are the values of \(a\), \(b\), \(m\) and \(n\)?

a =

b =

m =

n =

\({ (\frac { { 9x }^{ 5 } }{ { 4y }^{ 7 } } ) }^{ -3 }=\frac { 1 }{ { (\frac { { 9x }^{ 5 } }{ { 4y }^{ 7 } } ) }^{ 3 } } =1\times { (\frac { { 4y }^{ 7 } }{ { 9x }^{ 5 } } ) }^{ 3 }=\frac { { ({ 4y }^{ 7 }) }^{ 3 } }{ { ({ 9x }^{ 5 }) }^{ 3 } } =\frac { 64{ y }^{ 21 } }{ 729{ x }^{ 15 } } \)
9

If \({ (\frac { { 4a }^{ 3 }\times 2{ a } }{ { 12{ a }^{ 4 }\times a } } ) }^{ -3 }=\frac { { ma }^{ n } }{ x{ a }^{ y } } \), what are the values of \(m\), \(n\), \(x\) and \(y\)?

m =

n =

x =

y =

\({ (\frac { { 4a }^{ 3 }\times 2{ a } }{ { 12{ a }^{ 4 }\times a } } ) }^{ -3 }=\frac { 1 }{ { (\frac { { 4a }^{ 3 }\times 2{ a } }{ { 12{ a }^{ 4 }\times a } } ) }^{ 3 } } =1\times { (\frac { 12{ a }^{ 4 }\times a }{ { { 4a }^{ 3 }\times 2{ a } } } ) }^{ 3 }={ (\frac { { 12a }^{ 5 } }{ { 8{ a }^{ 4 } } } ) }^{ 3 }=\frac { { { ({ 12a }^{ 5 }) }^{ 3 } } }{ { { (8a }^{ 4 }) }^{ 3 } } =\frac { 1728{ a }^{ 15 } }{ 512{ a }^{ 12 } } \)
10

If \(\frac { 5 }{ { a }^{ 4 } } \times { 3a }^{ 8 }=m{ a }^{ n }\), what are the values of \(m\) and \(n\)?

m =

n =

\(\frac { 5 }{ { a }^{ 4 } } \times { 3a }^{ 8 }=5{ a }^{ -4 }\times { 3a }^{ 8 }=15{ a }^{ -4+8 }=15{ a }^{ 4 }\)
 

Amortisation and Annuities

1

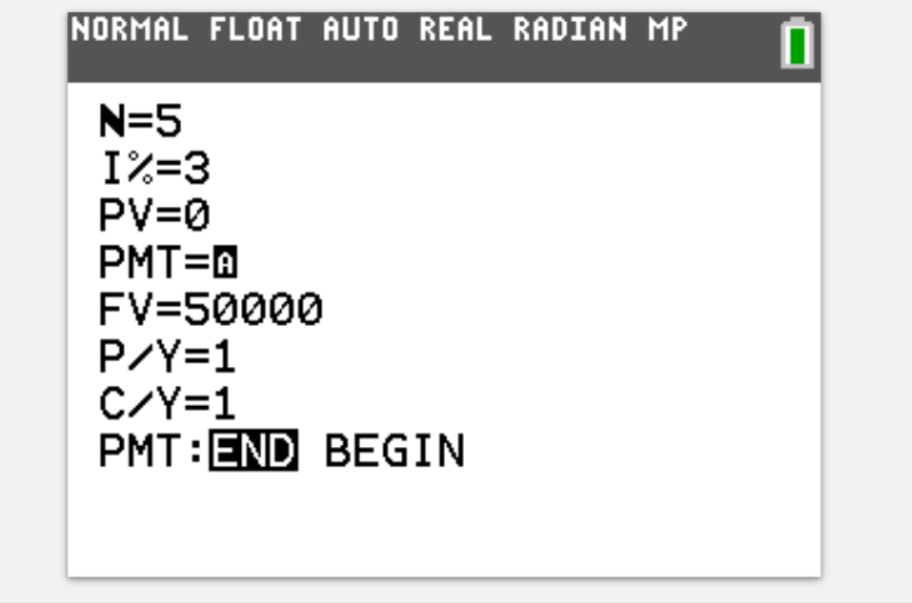
Katie wants to save to put a deposit of $50000 down on a house in five years. She saves every year in an annuity that gives 3% interest. Calculate how much she needs to save each year (to 3sf)

$

2

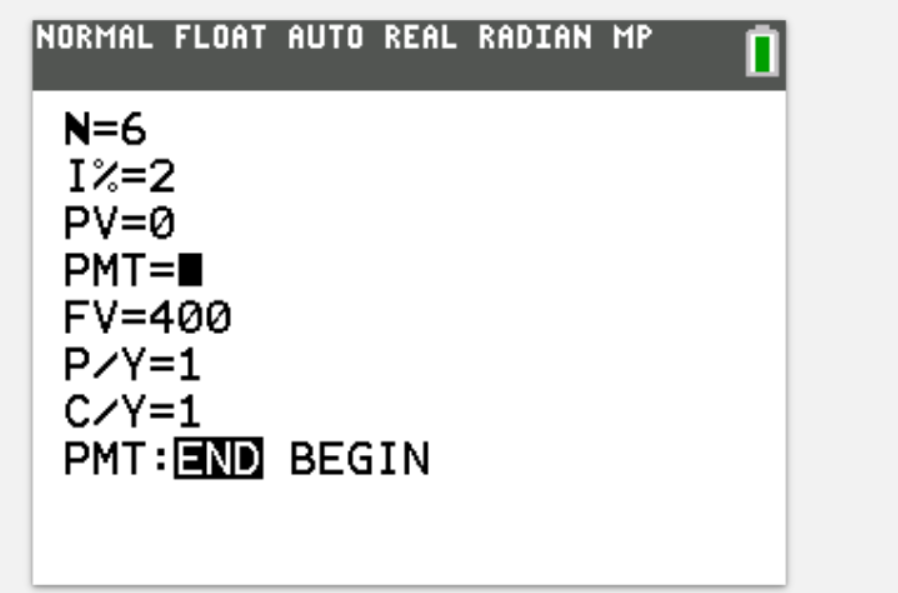
Joe is saving to buy a new pizza oven, which costs $400. He would like to buy it six months time. He saves every month in an annuity that gives 2% interest. How much does he need to save each month? (to 2dp)

$

3

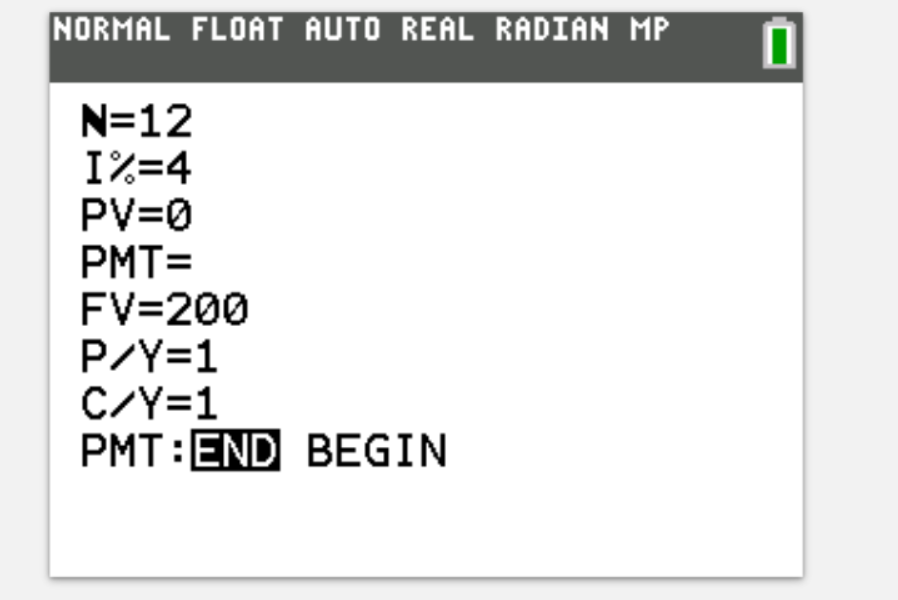
Adrian is saving to buy a record player, which costs $200. He would like to buy it a year's time, and saves every month in an annuity that gives 4% interest. How much does he need to save each month? (to 2dp)

$

4

Diane is saving to buy an expensive painting, which is valued at $1,000,000. She would like to buy it in 5 years time and saves each year in an annuity that gives 7% interest. Calculate how much she needs to save each year (to 2 dp)

$

 

Accuracy and Estimation

1

Which of the following is 14.7854 correctly rounded to 3 significant figures

14.8 - the third non zero digit is 7, which is rounded up to 8 because of the 8 that follows

2

Which of the following is 0.003046 correctly rounded to 3 significant figures

0.00305 - the third non zero digit is 4, which is rounded up to 7 because of the 6 that follows

3

Which of the following is 12348 correctly rounded to 3 significant figures

12300 - the third non zero digit is 3, which stays the same because of the 4 that follows

4

Which of the following is 6504905 correctly rounded to 3 significant figures

6500000 - the third non zero digit is 0, which stays the same because of the 4 that follows

5

Which of the following is 452756 correctly rounded to 3 significant figures

453000 - the third non zero digit is 2, which becomes 3 because of the 7 that follows

6

A rectangular field measures 23m by 63m, correct to the nearest metre. What is the smallest possible area of the field in square metres? (Give the exact answer)

The lower limt of both measurements are 22.5 and 62.5.

22.5 x 62.5 = 1406.25

7

A rectangular field measures 15m by 21m, correct to the nearest metre. What is the upper limit for the area of the field in square metres? (Round your answer to 3sf))

The upper limt of both measurements are 15.5 and 21.5.

15.5 x 21.5 = 333.25, which is 333 when rounded to 3sf

8

A bucket is used to lower the level of water in a swimming pool - 100 full buckets were removed. The bucket is advertised with a capcity of 3 litres, The actual capacity of the bucket is 3.2 litres. What is the percentage error if the marketed capacity is used to calculate the volume of water that is removed?

\(Volume\quad using\quad marketing\quad capacity\quad =\quad 300l\\ Actual\quad volume\quad =\quad 320l\\ Percentage\quad error\quad =\quad \frac { 320-300 }{ 320 } \times 100=6.25\)

9

Hannah estimates that the sum of the first 20 terms of the following sequence, \({ U }_{ n }=12+8(n-1)\), is 2000. What is her percentage error

\({ U }_{ n }=12+8(n-1)\\ n=20,\quad { U }_{ 1 }=12,\quad d=8\\ S_{ 20 }=\frac { 20 }{ 2 } (24+8(20-1))=1760\\ Error\quad =\quad \frac { 2000-1760 }{ 1760 } \times 100=13.6\quad (3sf)\)

10

Nick converted 300 Zambia Kwechas (ZMW) to Euros (EUR) and the bank were offering an exchange rate of 1 ZMW = 0.049 EUR. If he converted 300 and got 14 EUR, how much commission was he charged?

The conversion rate is

\(1\quad ZMW\quad =\quad 0.049\quad EUR\)

so converting 300 ZMW gives:

\(300\quad ZMW\quad =\quad 14.7\quad EUR\)

Buzz got 14 so he paid 0.7 EUR in commission, making the percentage difference:

\(\frac{0.7}{14.7}\cdot100=4.76\)

 

Standard Form

1

Convert the speed of light, \(300000000\space ms^{-1}\), into standard form.

The first number has to be a number between \(1\) and \(10\)(\(10\) not included). If we insert a decimal point after the digit \(3\), then count how many times we must move that point to get to the end of the number, that provides the power of \(10\) required.

2

Write 50200 in the form \(a\times 10^{k}, where\space 1\leq a<10\space and\space k \in \mathbb{Z}\).

The first number has to be a number between \(1\) and \(10\)(\(10\) not included). If we insert a decimal point after the digit \(5\), then count how many times we must move that point to get to the end of the number, that provides the power of \(10\) required.

3

The population of Beijing is approximately \(21.5\) million people. Write this in standard form.

Since \(1\) million is \(10^6\), we start by writing the number as \(21.5\times10^{6}\). The first number has to be a number between \(1\) and \(10\)(\(10\) not included), we must divide it by \(10\). To balance out that division so as not to change the number, we must multiply \(10^6\) by \(10\). This gives the answer shown.

4

Convert \(1.2\times10^{3}\) into normal form.

Start by writing out the first number, \(1.2\), and since the power is \(3\), move the decimal point to the right \(3\) places. Then fill in the gaps with zeros.

5

Convert \(5.5\times10^{-4}\) into normal form.

Start by writing out the first number, \(5.5\), and since the power is minus \(4\), move the decimal point to the left \(4\) places. Then fill in the gaps with zeros.

6

The average width of a red blood cell is \(0.006\space mm\). Write this in the form \(a\times 10^{k}, where\space 1\leq a<10\space and\space k \in \mathbb{Z}\).

The first number has to be a number between \(1\) and \(10\)(\(10\) not included). If we insert a decimal point after the digit \(6\), then count how many times we must move that point to get to the decimal, that provides the power of \(10\) required.

7

How many zeros are there beteen the decimal point and the first significant figure of \(4.63\times10^{-12}\)?

The number given is \(0.00000000000463\). There are \(11\) zeros between the decimal point and the first significant figure.

8

Water flows through a tube at a rate of \(12\space ms^{-1}\). How long will it take to fill a pool with volume \(1.7\times10^{3}\space m^{3}\)? Leave your answer to the nearest second.

Division: \((1.7\times10^{3})\div12=141.667 s\). The answer is shown to the nearest second.

9

It takes light approximately 8 minutes to reach the Earth from the Sun. If light travels at \(3\times10^{8}\space ms^{-1}\), calculate the distance between the Earth and the Sun. Give your answer in km, written in standard form.

Since \(8\) minutes is \(420\) seconds, multiply \(3\times10^{8}\times420=1.44\times10^{11}\space m\). To change metres into kilometres, we divide by \(1000\). However, dividing by \(10^{3}\) is equivalent to subtracting \(3\) from the power, leaving \(1.44\times10^{8}\space km\).

10

Write \(600.7\times10^{-6}\) the form \(a\times 10^{k}, where\space 1\leq a<10\space and\space k \in \mathbb{Z}\).

\(a=\)

\(k=\)

Since the first number has to be a number between \(1\) and \(10\)(\(10\) not included), we must divide it by \(100\) or \(10^{2}\). To balance out that division so as not to change the number, we must multiply \(10^{-6}\) by \(10^2\). This gives the answer shown.

 

Arithmetic Sequences

1

Which of the following sequences could be arithmetic

Arithmetic sequences must have a constant difference between the terms. Four of the answers do not. The others could be arithmetic sequences because they do.

2

What is the common difference in this sequence? 2, 1.8, 1.6, 1.4 (no spaces in your answer)

Sequence goes down by 0.2 each time so the difference is -0.2

3

The general term of an arithmetic sequence is given by Un = 3 + 4(n - 1), what is the 10th term of this sequence?

Substitute n = 9 into the nth term and get U10 = 3 + 4 X 9, so U10 = 39

4

Consider the following sequence, Un = -2 + 0.5(n - 1), work out the 8th and 15th terms and add them together.

Substitute n = 8 and 15 in to the general term. The 8th term is 1.5, 15th term is 5, together they sum to 6.5

5

An arithmetic sequence begins 5, 14, 23, 32..... Which of the following is the nth term of that sequence

Using the formula for the nth term, Un = U1 + d(n - 1), substitue U1 = 5 and d = 9

6

Consider the arithmetic sequence that begins 15, 31, 47.... Calculate the sum of the the first ten terms of this sequence.

Substitue U1 = 15 and d = 16 in to the sum formula, or work out that U10 = 159 and use the other formula

7

Calculate the sum of the first 20 terms of this sequence Un = 10 - 4(n - 1)

Substitue U1 = 10 and d = -4 in to the sum formula, or work out that U20 = -66 and use the other formula

8

An arithmetic sequence has U4 = 18 and U7 = 30, what is the first term of the sequence?

Work out that the common difference ias added 3 times between the 4th and 7th term and this is +12 all together so d = 4. Subtract the value of d 3 times to get back to the first term.

9

An arithmetic sequence has U2 = 18 and U9 = 53, what is the 10th term of the sequence?

Work out that the common difference ias added 7 times between the 2nd and 9th term and this is +35 all together so d = 5. Add the value of d once to get from the 9th to 10th terms.

10

Which is greater,

a) The sum of the sequence Un = 150 + 25(n - 1) to the first 20 terms or

b) The sum of the sequence Un = 150 + 20(n - 1) to the first 25 terms

The first sum is 7750 and the second is 9750

 

Geometric Sequences

1

Which of the following sequences could be geometric?

Onnly the sequences where each term is found by multiplying the previous term by the same common ratio. Example, 5, 10, 20 works because each term is the previous term multiplied by 2.

2

What is the common ratio of this geometric sequence?

7, 21, 63, 189

7 x 3 = 21, 21 x 3 = 63, 63 x 3 = 189

3

What is the next term of this geometric sequence?

4, 6, 9.....

Each term is 1.5 times bigger than the previous term

4

What is the 6th term of the geometric sequencethat begins 3, 15, 75 ?

3 x 55 = 9375

5

What is the 10th term of the geometric sequence Un = 2.5 x (-2)(n-1)

2.5 x (-2)9

6

Which of the following could be the nth term of the geometric sequence that begins...... 2, 8, 32, 128?

The general expression for the nth term of a geometric sequence is Un = U1 x r(n-1), where U1 is the first term, r is the common ratio and n is the postion/number of terms. We can see that the common ratio is 4 and the first term is 2.

7

Which of the following sequences could be a part of the geometric sequence with the general expression Un = 3 x 2(n-1)?

6, 12, 24 are the first 3 terms. If you divide the terms 192, 384, 768 by 3 (the first term) you get 64, 128, 256, which are successive powers of 2 and so each of these terms are 3 x a power of 2 and so they must be part of the sequence.

8

Consider the geometric sequence that begins 4.5, 9, 18....

What is the sum of the first 8 terms of this sequence?

Substitute n = 8, U1 = 4.5 and r = 2 in to the sum formula.

\({ S }_{ n }={ u }_{ 1 }\left( \frac { { r }^{ n }-1 }{ r-1 } \right) \\ in\quad this\quad case,\quad { u }_{ 1 }=4.5\quad and\quad r=2\\ SO,\\ { S }_{ 8 }=4.5\left( \frac { { 2 }^{ 8 }-1 }{ 2-1 } \right) \\ { S }_{ 8 }=4.5\left( \frac { 255 }{ 1 } \right) \\ { S }_{ 8 }=1147.5\)

9

What is the sum of the first 20 terms of this geometric sequence, Un = 15 x 1.2(n - 1). Give you answer correct to 3 sf.

Substitute n = 20, U1 = 15 and r = 1.2 in to the sum formula. Then round carefully.

\({ S }_{ n }={ u }_{ 1 }\left( \frac { { r }^{ n }-1 }{ r-1 } \right) \\ in\quad this\quad case,\quad { u }_{ 1 }=15\quad and\quad r=1.2\\ SO,\\ { S }_{ 20 }=15\left( \frac { { 1.2 }^{ 20 }-1 }{ 1.2-1 } \right) \\ { S }_{ 20 }=2800.319994\\ { S }_{ 20 }=2800\quad (3sf)\)

10

A geometric sequence has U3 = 9 and U6 = -243, what is its common ratio?

\({ u }_{ 3 }\times { r }\times { r }\times { r }={ u }_{ 6 }\\ { u }_{ 3 }\times { r }^{ 3 }={ u }_{ 6 }\\ 9\times { r }^{ 3 }=-243\\ { r }^{ 3 }=\frac { -243 }{ 9 } =-27\\ r=\sqrt [ 3 ]{ -27 } =-3\)

Functions

Trigonometric Models

1

On a unit circle, \(\sin\left(30\right)\) represents...

See answer given.

2

The period of the function, \(f\left(x\right)=\cos\left(x\right)\), is...

3

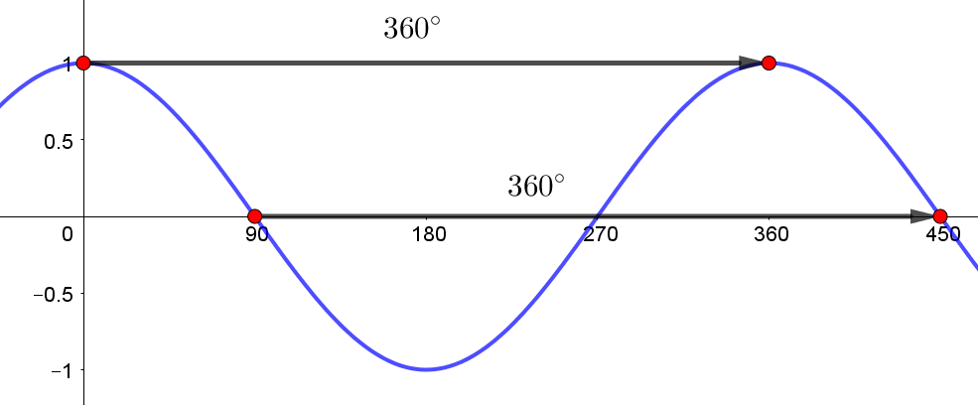
The period of the function, \(f\left(x\right)=\cos\left(2x\right)\), is...

Utilising the formula, \(Period=\frac{360}{b}\);

\(Period=\frac{360}{2}=180 ^{\circ}\)

4

The period of the function, \(f\left(x\right)=2\cos\left(x\right)\), is...

In this function the amplitude has doubled but the period has not changed from \(f\left(x\right)=\cos\left(x\right)\).

5

A function is given by \(f\left(x\right)=4\cos\left(kx\right)\). If the period of the function is 120 degrees, find the value of \(k\).

Utilising the formula, \(b=\frac{360}{Period}\);

\(b=\frac{360}{120}=3\)

6

A function, \(g\), is given by \(g\left(x\right)=3\sin\left(4x\right)+2\).

Identify the amplitude, period and principal axis of \(g.\)

, Period: \(90\) degrees; Principal Axis: \(y=2\)

, Period: \(4\), Principal Axis: \(y=2\)

The point of this question is to show that the \(4\) inside the brackets is not itself the period of the wave, but it does of course affect the period.

7

A function, \(g\), is given by \(g\left(x\right)=\sin\left(10x\right)-1\).

Identify the amplitude, period and principal axis of \(g.\)

Amplitude:

Period:

Principal Axis:

See answers given.

8

A function, \(g\), is given by \(g\left(x\right)=5\sin(\frac{x}{2})\).

Identify the amplitude, period and principal axis of \(g.\)

Amplitude:

Period:

Principal Axis:

In this case for the period, rewrite \(\frac{x}{2}\) as \(\frac{1}{2}x\) and utilise the formula, \(Period=\frac{360}{b}\);

\(Period=\frac{360}{0.5}=720 ^{\circ}\). Other answers are given and more easily understood.

9

The equation of the curve below is given as, \(f\left(x\right)=a\cos\left(bx\right)+c\).

Find the values of \(a\), \(b\) and \(c\).

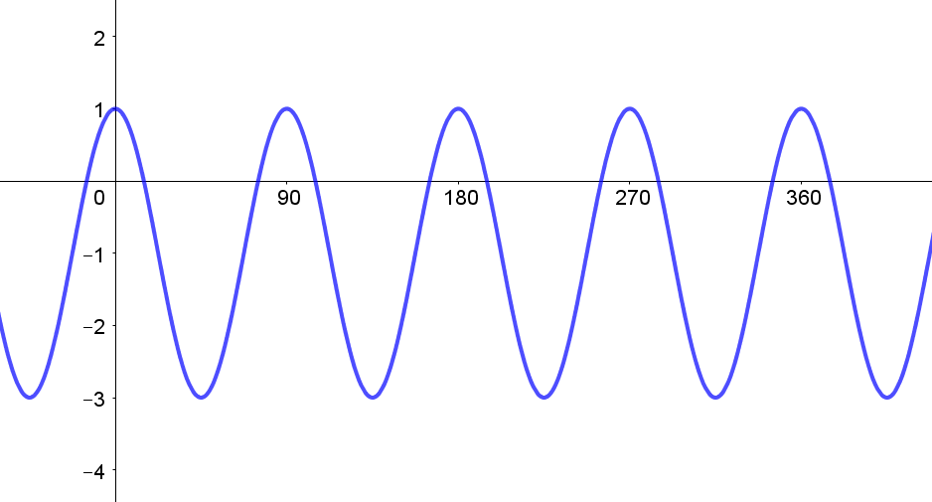
a:

b:

c:

You can use the equations given in video 4, or find these values more intuitively.

The principal axis (or centre line) or the curve is the most logical to identify first. This corresponds to the value \(c\) which is \(-1\).

The amplitude is the height between the principal axis and the maximum (or minimum points. This corresponds to the value \(a\) which is \(2\).

The period of the wave is \(90\) degrees. Intuitively this means that \(4\) waves fit into a \(360\) degree domain which means that the value \(b\) is \(4\). You might also find this using \(b=\frac{360}{Period}\);

\(b=\frac{360}{90}=4\).

10

The equation of the curve below is given as, \(f\left(x\right)=a\sin\left(bx\right)+c\).

Find the values of \(a\), \(b\) and \(c\).

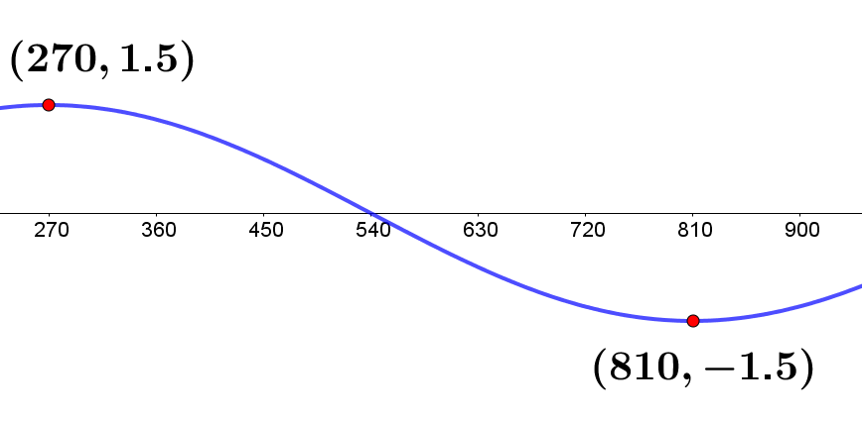
Utilising the formulae in this case:

\(a=\frac{\max-\min}{2}=\frac{1.5--1.5}{2}=\frac{3}{2}=1.5\)

To find \(b\), first identify the period of the wave. Half of the wave is shown with the co-ordinates given, so half the period is \(810-270=540\). The period is therefore \(540\cdot2=1080\). Hence, \(b=\frac{360}{1080}=\frac{1}{3}\).

\(c=\frac{\max+\min}{2}=\frac{1.5+-1.5}{2}=\frac{0}{2}=0\)

 

Key Features of Functions and Graphing

1

What can you call the points shown on the diagram below?

The only incorrect response to this question is "vertices".

2

A function, \(f\), is defined by \(f\left(x\right)=x^{2}+6x+3\)

Find the x-intercepts of the graphs of \(f\)

Answers: ,

Notice that the answers have not been given as co-ordinates. This is strictly correct, but not necessary in an exam scenario. Answers should also be given to 3 s.f. where appropriate.

3

Which of these function contain a vertical asymptote? (there is more than one correct answer)

Only the first two rational functions contain vertical asymptotes (they also contain horizontal asymptotes). The exponential function, \(f\left(x\right)=3^{x}-2\), contains a horizontal asymptote but no vertical asymptote.

4

Tick the answers below which are most commonly required when you are asked to "sketch a graph."

A sketch requires you to be relatively accurate, but it does not require the same level of detail as when you are asked to "draw a function."

5

Tick the answers below which are most commonly required when you are asked to "draw a graph."

Drawing a graph requires precision, hence why all answers above are correct.

6

The formuala, \(A=\pi{r}^{2}+\frac{100}{r}\), is given for the surface area, \(A\), of a cylinder with radius, \(r\).

Find the local minimum point which minimises the surface area.

Minimum Surface Area: \({cm}^2\)

Graph the function in your GDC and identify the local minimum. On the GDC you will be given (2.52, 59.6), but you can discard 2.52 given that this is the value of the radius, \(r\), which results in a minimum surface area, and that is not needed for the question.

7

Below is a sketch of the function, \(f\left(x\right)=\frac{1}{3}x^{3}+\frac{3}{4}x^{2}-x-1\)

Identify what is missing from the skecth below:

See answers given.

8

Consider the function, \(f\left(x\right)=3^{x}+\frac{1}{x+2}\)

Sketch the grap of \(y=f(x)\) for \({-2}\leq{x}\leq{2}\) and \({-2}\leq{y}\leq{10}\).

Type "done" into the textbook to check your answer:

9

Consider the functions \(f\left(x\right)=x+2\) and \(g\left(x\right)=3^{x}-3\)

Solve \(f\left(x\right)=g\left(x\right)\).

Answers: ,

When you graph the two functions, there are two points of intersection, (-5.00, -3.00) and (1.74, 3.74).

10

Finish the sentence -

A straight line can intersect a quadratic function in:

See answers.

 

Introducing Functions

1

Is this a function or a relation?

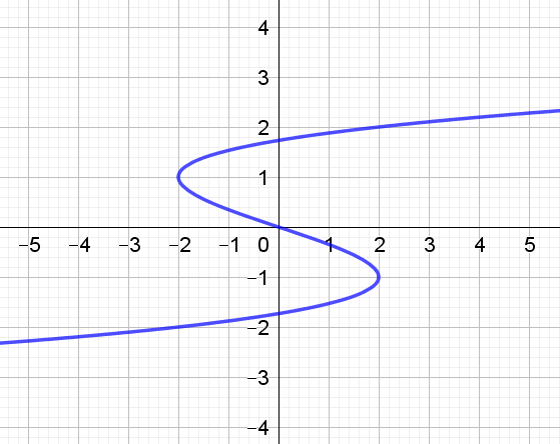
Since it fails the vertical line test - i.e. there is a section in which a vertical line passes through more than one point on the curve - it must be a relation.

2

Identify which functions are linear.

Linear functions - which are straight lines on a co-ordinate grid - have an \(x\) term with a maximum power of \(1\), which we of course do not write in mathematics. \(w(x)\) is a quadratics function, \(q(x)\) is a rational function and \(v(x)\) is an exponential function.

3

Consider the function \(f(x)=\frac{1}{3}x^2+\frac{2}{5}x-2\)

Find \(f(2)\), giving your answer to 3 significant figures.

If you substitute \(x=2\) into the functin you obtain 0.133.

4

A toy sales person sells \(t\) toys per month.

Her monthly profit in US dollars can be modelled by: \(N(t)=t^3+2t-100\)

Find the value of \(N\) if no toys are sold.

If no toys are sold, \(t=0\), and hence \(N(0)=-100\) dollars.

5

Consider the function \(f(x)=\frac{3+x}{x^2}\)

A point \((x, 14)\) lies on this function. Find the value of \(x \)

Start by substituting \(14\) into the equation: \(14=\frac{3+x}{x^2}\)

Using your GDC, graph each side of the equation and find the point of interestion of these graphs.

Since we are only interested in the \(x\space co-ordinate\) of that intersection point, you find \(x=0.25\)

6

If you know that \(f(10)=25\), find \(f^{-1}(25)\)

If \(f\) takes an input of \(10\) and produces an output of \(25\), then the inverse of \(f\), \(f^{-1}\), does the opposite.

7

Find the domain of the function, \(f(x)=\sqrt{x}\)

If you input the graph of \(f(x)=\sqrt{x}\) into your GDC, you will notice that it does not exist for any negative value of \(x \), because we cannot take the square root of a negative number and obtain a real answer. The domain is therefore, \(x \geq 0\).

8

Find the range of the function \(f(x)=x^2\)

If you completed the previous question, then you will already be aware the the domain of a function, is the same the range of its inverse. Therefore, the range of \(f(x)=x^2 \) is \(f(x) \geq0\). This can also been seen through inputting the graoh into your GDC, or noting that when you square any input number, the output will always be positive or zero.

9

What can you say about the domain and range of any diagonal straight line (linear function).

Domain:

Range:

Choose options below to write into the text input boxes - note that it may be the same option.

a. all real numbers

b. x / f(x) must be greater than zero

c. x / f(x) must be less than zero

The domain and range of diagonal straight lines is all real numbers. This is not the case for horizontal or vertical lines.

10

To graphically obtain an inverse function, you reflect it on the co-ordinate grid in the diagonal line, .....................................

To obtain the inverse function graphically, reflect it in the diagonal line, y = x.

 

Sinusoidal Functions

1

Match the functions shown in the diagram below with the letters

Drag the correct letter in the box A B C D

sinx is graph

sin2x is graph

2sinx is graph

sinx+2 is graph

2

Match the functions shown in the diagram below with the letters

Drag the correct letter in the box A B C D

cos3x is graph

0.5cosx is graph

2cosx is graph

cosx is graph

3

Consider the following sinusoidal function \(f(x)=asinbx+c\) as shown in the diagram below. Determine the values of a, b and c

a= b= c=

4

Consider the following sinusoidal function \(f(x)=asinbx+c\) as shown in the diagram below. Determine the values of a, b and c

a= b= c=

5

Consider the following sinusoidal function \(f(x)=asinbx+c\) as shown in the diagram below. Determine the values of a, b and c

a= b= c=

6

Consider the following sinusoidal function \(f(x)=acosbx+c\) as shown in the diagram below. Determine the values of a, b and c

a= b= c=

Watch out! For cos functions, the y-intercept is c+a

7

Consider the following sinusoidal function \(f(x)=acosbx+c\) as shown in the diagram below. Determine the values of a, b and c

a= b= c=

Watch out! For cos functions, the y-intercept is c+a

8

Consider the following sinusoidal function \(f(x)=acosbx+c\) as shown in the diagram below. Determine the values of a, b and c

a= b= c=

Watch out! For cos functions, the y-intercept is c+a

 

Quadratic Models

For the first seven questions of the is queuiz you need to refer to the quadratic function y = x2 -2x - 15 and its graph, drawn below,

1

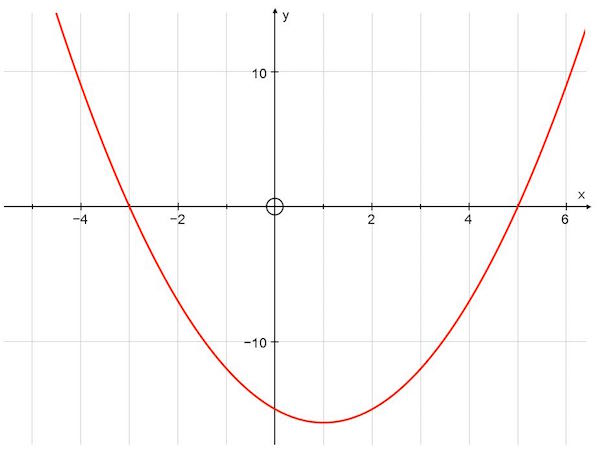
What is the exact value of y, when x = 2.5? (do not include spaces in your answer)

Type the function in to your GDC, use the table menu, set the table to go up in steps of 0.5 and read the answer from the table. OR, use the the 'value' or 'y solve' tool on your GDC.

......

2

What is the exact value of x, when y = 128? (do not include spaces in your answer)

Type the function in to your GDC, use the table menu, set the table appropriately and read the answer from the table. OR, use the 'x solve' tool on your GDC.

3

Which of the following is the correct factorisation of the given quadratic?

Expand the brackets to be sure. SInce the coefficient of x is -2, this must come from +3, -5. SInce the value of 'c' is - 15, this corresponds.

4

Use your GDC to find the 'zeros' or 'roots' of this quadratic equation. What are the coordinates of the positive root? Answer in the form (x,y) with no spaces.

USe the 'Calc' or 'gsolve' menu on your calculator and choose 'zeros' or 'roots'.

5

What are the coordinates of the y-intercept of the function? Answer in the form (x,y) with no spaces.

The y - intercept occurs when x = 0. This leaves y = -15.

6

What is the equation of the axis of symmetry for this function? (no spaces)

The axis of symmetry is given by x = -b/2a, where y = ax2 + bx + c

7

Use your GDC, or otherwise, to work out the coordinates of the vertex of the function. (no spaces)

Ues the 'calc' or 'gsolve' menu on your calculator and choose 'min'. Alternatively, sonce you know the axis of symmetry is x = 1, work out the value of y when x = 1.

8

Which of the following functions is shown in the diagram below?

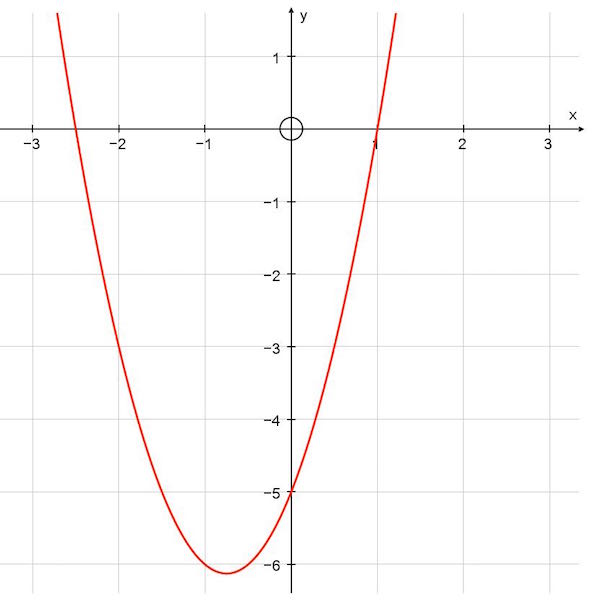
We can see that the function intersects th y axis at (0,-5) and so c = -5. This narrows it down to 2 functions. You can see the the function has zeros at x = -2.5 and 1. These values of x should give y = 0 when substituted.

9

The profit (P) in dollars made by a given enterprise is given by 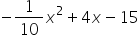negative 1 over 10 x squared plus 4 x minus 15 where x is the number units sold. What was the cost of their intial investment? How many units need to be sold before they break even. (this means they have covered their costs - answer should be a whole number)

Cost of initial investment dollars

Number of units sold to break even units

The initial investment is the money they spent before anything was sold. This is the y value when x = 0 , in other words, the y-intercept. The number of units for breakeven is the value of the first zero. Up until that point, the profit is negative. 5 is the fisrt whole number x - value that yields a profit of greater than or equal to zero.

10

The profit (P) in dollars made by a given enterprise is given by 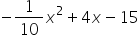negative 1 over 10 x squared plus 4 x minus 15 where x is the number units sold. What is the maximum profit that can be made with this model? How many units need to be sold for this maximum profit?

Maximum profit

Number of units

The maximum profit is the y coordinate of the maximum point on the curve. The number of units is the corresponding x coordinate. Use your GDC to find these values.

 

Exponential Models

1

Consider the exponetial function 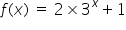f left parenthesis x right parenthesis space equals space 2 cross times 3 to the power of x plus 1,

Fill in the corresponding values of the function for the given values of x.

x = 0, so f(x) =

x = 5, so f(x) =

Either substitue the value of x in to the function and calculate directly OR type the function in to your GDC and read your answers from the table. Note a0=1.

2

Consider the exponetial function 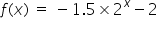f left parenthesis x right parenthesis space equals space minus 1.5 cross times 2 to the power of x minus 2,

Fill in the corresponding values of the function for the given values of x. (give exact answers)

x = 1 so f(x) =

x = -2, so f(x) =

Either substitue the value of x in to the function and calculate directly OR type the function in to your GDC and read your answers from the table. Note a0=1.

3

Write down the y-coordinate of the y-intercpt and the equation of the asymptote for the following exponential function.

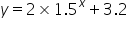
y equals 2 cross times 1.5 to the power of x plus 3.2

The y-intercept is at (0, )

The asymptote has the equation y =

For the y - intercept, substitute x = 0. So, 1.50 = 1 therefore y = 2 + 3.2. SInce 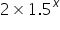2 cross times 1.5 to the power of x can never be zero, y can never be 3.2

4

Write down the y-coordinate of the y-intercpt and the equation of the asymptote for the following exponential function.

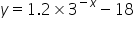
y equals 1.2 cross times 3 to the power of negative x end exponent minus 18

The y-intercept is at (0, )

The asymptote has the equation y =

For the y - intercept, substitute x = 0. So, 30 = 1 therefore y = 1.2 -18. SInce 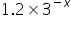1.2 cross times 3 to the power of negative x end exponent can never be zero, y can never be -18

5

Consider the graphs on the axes below. Write the corresponding letter next to each function. (use upper case)

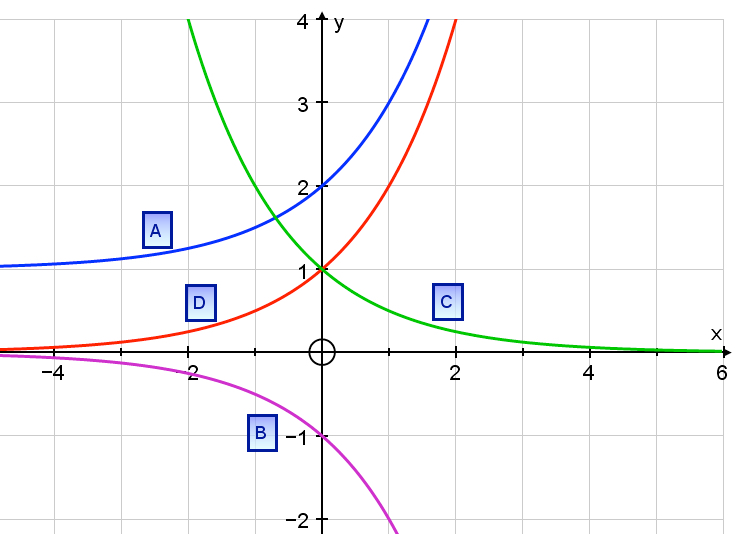
y = 2x ,

y = 2x+1,

y = -2x,

y = 2-x,

You can simply put these in your calculators. BUT you should recognises that A is the same as D but moved 1 up the y - axis. C has -x in the exponent to produce that reflection and B is -2x , the negative of 2x .

6

An experiment is done to monitor how a population of bacteria grows over time. At the start, there are 200 bacteria and they triple every hour. If the function we would use to model this is in the form 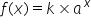f left parenthesis x right parenthesis equals k cross times a to the power of x , what are the values of k and a?

k =

a =

200 must be the starting value, when x = 0. Next, 3 is the multiplier because the population triples for every x-increase by one.

7

The value of a car depreciates by 20% each year after purchase. It was purchased for $4000. If the function we would use to model this is in the form 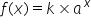f left parenthesis x right parenthesis equals k cross times a to the power of x , what are the values of k and a?

k =

a =

4000 must be the starting value, when x = 0. Next, 0.8 is the multiplier because the value becomes 80% of its previous value with each passing year.

8

Consider the model 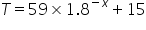T equals 59 cross times 1.8 to the power of negative x end exponent plus 15, which measures temperature (T) as time (x, in minutes) passes.

What is the initial temperature at the start of the experiment?

T =

This is when x = 0.

9

Consider the model 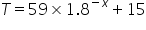T equals 59 cross times 1.8 to the power of negative x end exponent plus 15, which measures temperature (T) as time (x, in minutes) passes.

What is the temperature after 4 minutes? (3sf)

T =

This is when x = 4. Read this from the table on your GDC.

10

Consider the model 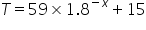T equals 59 cross times 1.8 to the power of negative x end exponent plus 15, which measures temperature (T) as time (x, in minutes) passes.

After how many minutes does the temperature fall below 18 degrees? (nearest minute)

After minutes.

Read this from the table on your GDC.

 
 

Statistics and Probability

Goodness of Fit and T-tests

1

A Chi-sqaured goodness of fit test has a p-value of 0.0231. If the test is conducted at a 5% significance level, what is the conclusion of the test.

, we reject the null hypothesis.

, we accept the null hypothesis.

If the p-value is less than or equal to the significance level, we reject the null hypothesis.

2

A t-test is has a p-value of 0.516. If the test is conducted at the 5% significance level, what is the conclusion of the test.

, we reject the null hypothesis.

, we accept the null hypothesis.

If the p-value is greater than the significance level, we accept the null hypothesis.

3

The formula for the degrees of freedom of a Chi-Squared goodness of fit test is:

See answer above.

4

When conducting a 2-sample t-test on your GDC, you start by inputting the data for each sample into your lists. The calculator will then ask you whether the data is Pooled. Which answer do you enter?

See answer above.

5

When conducting a 2 sample t-test, what assumptions do you make in performing a test?

See answers above.

6

A school decided to pilot a reward based system if students attended over 95% of the academic year. Any students in year 10 who attended over this percentage would be allowed to go on a reward trip. At the end of the year, the school decided to compare the year 10 attendance results with that of the previous year 10. It was assumed that students in the current year would be motivated by the reward trip and therefore attend school more regularly.

The analysis involved a t-test. What type of test would this involve?

This is a one-tailed test because we are hypothesising that the mean of the current group of year 10 students is going to be greater than the mean of the previous group of year 10 students. i.e. we have been given information in the question which suggests that one data set will have a higher mean than the other.

7

A school decided to pilot a reward based system if students attended over 95% of the academic year. Any students in year 10 who attended over this percentage would be allowed to go on a reward trip. At the end of the year, the school decided to compare the current year 10 attendance results with that of the previous year 10. It was assumed that students in the current year would be motivated by the reward trip and therefore attend school more regularly. A sample was taken of eacy year group and the results are shown below:

Current Year 1090%96%96%96%92%100%100%99%97%99%
Previous Year 1090%95%89%90%96%97%100%90%93%92%

Conduct a t-test and identify the p-value for this data. Give your answer to 3 significant figures.

p-value:

Insert each data set into a list, then perform a 2 sample t-test, with \(\mu_1>\mu_2\). Ensure you enter "Yes" on Pooled data.

8

For a Chi-squared goodness of fit test, the critical value is given as 14.1. The \(χ_2 \) statistic iscalculated to be 10.5. Identify the conclusion for the test.

See answer above.

9

For football stickers, the manufacturer claims the following distribution for the proportions of sticker type:

Rarity of StickerPercentage
Very Common50%
Common35%
Rare10%
Very Rare5%

Sophie is skeptical of the manufacturers claim and tests the result on 200 stickers based on the sticker website information. Her results are shown below:

Rarity of StickerFrequency
Very Common110
Common79
Rare7
Very Rare4

Find the expected frequency of how rare each category of sticker is.

Rarity of StickerExpected Frequency
Very Common
Common
Rare
Very Rare

To find the expected frequencies, multiply the total number of trials by the expected proportions. i.e.

Rarity of StickerExpected Frequency
Very Common\(200\times0.5\)
Common\(200\times0.35\)
Rare\(200\times0.1\)
Very Rare\(200\times0.05\)
10

For football stickers, the manufacturer claims the following distribution for the proportions of sticker type:

Rarity of StickerPercentage
Very Common50%
Common35%
Rare10%
Very Rare5%

Sophie is skeptical of the manufacturers claim and tests the result on 200 stickers based on the sticker website information. Her results are shown below:

Rarity of StickerFrequency
Very Common110
Common79
Rare7
Very Rare4

Conduct a Chi-Squared goodness of fit test to determine whether the manufacturers claims are correct. Enter the p-value in the space below, given to 3 significant figures, and determine the conclusion of the test at a 1% significance level.

Degrees of Freedom:

p-value:

Since 0.00264 < 0.01, we reject the null hypothesis which means that the manufacturers claim about the proportions of sticker types is incorrect.

 

Spearman's Rank

1

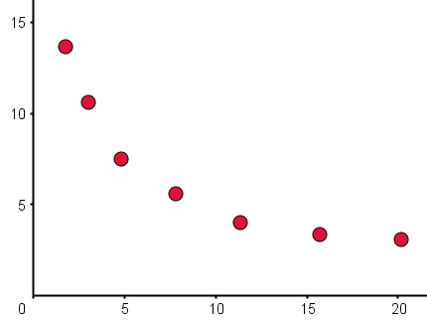
Estimate Spearman's rank correlation coefficient, \(r_{s}\), for the following scatter graph.

The data is strictly increasing, with the exeption of the final point, and given that the final point is still relatively close to the previous point, \(r_{s}\), is high.

2

Estimate Spearman's rank correlation coefficient, \(r_{s}\), for the following scatter graph.

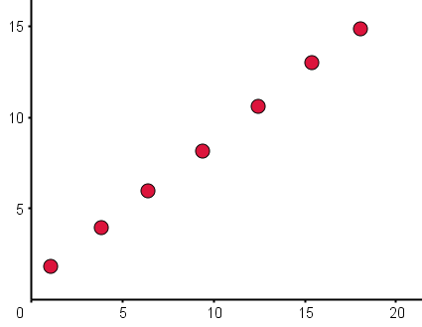
Given the data is strictly increasing (monotonic), \(r_{s}\) equals one.

3

Estimate Spearman's rank correlation coefficient, \(r_{s}\), for the following scatter graph.

Given the data is strictly increasing (monotonic), \(r_{s}\) equals minus one.

4

Two judges score a diving competition with five competitors. After ranking the scores, the \(r_{s}\) value is found to be 0.952. Comment on \(r_{s}\)in this context.

See answer above.

5

The amount of time studying for a Biology test is compared with the assessment scores. The \(r_{s}\) value for the data was 0.650. Interpret this value.

See answer above.

6

Before calulating Spearman's Rank Correlation Coeffiient, we create a ranked table. Create a ranked table for the data below. Rank from smallest to largest.

x22538
y32347
Rank, x
Rank, y

Given that the first position and second position are equal for the variable x, we average these positions to get 1.5 in each case. This is similarly the case for the second and third position for variable y, giving 2.5 for these positions. Note that it is equally valid to rank from largest to smallest, as long as you do this for bothh variables.

7

The temperature of coffee is taken over time. The results are given in the table below.

Time (t), mins010203040
Temperature, T, celsius6845302525

Find \(r_{s}\)

The ranked table should be:

Rank Time12345
Rank Temperature5431.51.5

After inserting this data into your GDC, you find \(r_{s}\) to be - 0.975.

8

The table below shows a class sample of study time compared with scores on a test.

Study Time, t1153.514
Score, S686092706480

Fill in the gaps in the ranked table below.

Study Time, t 64 5
Score, S316425

 

Given that the first, second and third position for time spent studying are the same, we will find the average of these positions by adding them and dividing by three. In this case, that gives a rank of 2 for all three empty boxes.

9

From the list below, pick the advantages of using Spearman's rank correlation coefficient rather than Pearson's product moment correlation coefficient.

See answers above.

10

A set of data is strictly increasing. If the final data point is brought below the previous data point, but so that it is still above all other data points. How will this effect \(r_{s}\)?

See answer above.

 

Statistical Concepts

1

Which of these are examples of discrete data?

Discrete data is data that can be counted, continuous data is data that can be measured

2

Which of these are examples of continuous data?

Discrete data is data that can be counted, continuous data is data that can be measured

3

Which type of data is data that can be measured, and can take an infinite number of values?

data

continuous data is data that can be measured, whereas discrete data is data that is counted

4

Which type of data is data that can be counted, and could only take a finite number of values?

data

continuous data is data that can be measured, whereas discrete data is data that is counted

5

An is a value that lies outside other values.

6

Below is a table of students' test results. One of these results is an outlier.

Craig45%
Laura36%
Luisa56%
Josh98%
Maia40%
Becca42%

a. Whose test result is the outlier?

b. What is the mean if you remove the outlier?

a.

b. %

7

An outlier is a piece of data that is distant from the other data in a data set. It can occur because of inaccurate data collection, but also just through variation in the data that is collected. As statisticians, we can choose to either include or exlude outliers, depending on whether we think they contribute to our analysis. This decision can change how we interpret a data set, as it impacts how we calculate central tendency, especially the

8

Match the word to the correct description:

The whole group we are interested in
A collection of data from the whole population
A collection of data from part of the population

Census Population Sample

Use this optional field for teacher explanations.

9

Match the word to the correct description of different types of sampling

Randomly chosen data, but in the ratio of group size
Data chosen from a random starting point, and then at even intervals
Data picked randomly from a list
A sample created from individuals that fit certain required characteristics
A sample chosen by ease of collection
Systematic Quota SimpleConvenience Stratified

Use this optional field for teacher explanations.

10

What type of sampling are you using if you survey every fifth person who enters the room?

Use this field for hidden/teacher's explanations

 

Discrete Random Variables

1

The following table shows the probability distribution of a discrete random variable X.

X1234
P(X=x)0.20.3 x 0.4

Find the value of x.

The sum of probabilities in a probability distribution must be one (i.e. 100%). Therefore, 0.2+0.3+x+0.1=1 and so x=0.1.

2

The following table shows the probability distribution of a discrete random variable X.

X1234
P(X=x)0.30.40.20.1

Find E(X).

To find the expected value, E(X): \(1\times0.3+2\times0.4+3\times0.2+4\times0.1=2.1\)

3

Which of the following are examples of discrete random variables?

Discrete random variables can only take a countable number of values. The marks on a test and the score on a die are both countable and so they are discrete random variables. In contrast, lengths of leaves and heights of students are measured, and they can take an infinite number of values. They are not discrete random variables.

4

X is a discrete random variable. Find the value of k in the following probability distribution.

X123
P(X=X)k 2k3k

Leave your answer as a fraction (use a / between the numerator and denominator)

The sum of probabilities in a probability distribution must be one (i.e. 100%). Therefore, \(k+2k+3k=1\) and so \(6k=1\), which means \(k=\frac{1}{6}\).

5

The following table shows the probability distribution of a discrete random variable, A.

a2 345
P(A=a)xy 0.10.2

Given that E(A) = 3.4, find the value of x and y.

x =

y =

Given that we have two unknowns, we will create 2 simultneous equations to solve.

Equation 1: \(x+y+0.2+0.1=1\), and thus \(x+y=0.7\)

Equation 2: \(2\times x+3\times y+4 \times 0.1+5\times 0.2=3.4\), and thus \(2x+3y=2\)

Solving these linear simultaneous equations on the GDC, we obtain \(x=0.1\) and \(y=0.6\).

6

Based on last season's statistics, a football player has the following probability distribution for goal scoring, with the discrete random variable, Y, representing the number of goals per game.

y0123
P(Y=y)0.30.450.20.05

Find the expected number of goals he will score in the next game. Leave your answer to the nearest positive integer.

The expected value, \(E(X)=0\times0.3+1\times0.45+2\times0.2+3\times0.05=1 \).

7

The random variable \(X\) has a probability distribution given by the function, \(P(X=x)=\frac{2x}{k}, x=1,2,3\).

Find the value of the constant, \(k\).

If we substitute the given values of \(x \) into the function, we obtain the following table:

\(x \)1 2 3
\(P(X=x)\)\(\frac{2}{k}\)\(\frac{4}{k}\)\(\frac{6}{k}\)

Since the probabilities in a probability distribution add up to one, then \(\frac{2}{k}+\frac{4}{k}+\frac{6}{k}=1\), so that \(\frac{12}{k}=1\) and hence \(k=12\).

8

A survey was taken in a school asking how many hours, to the nearest hour, IB Diploma students studied for each night. Relative frequencies were calculated, and the table below shows the probability distribution. The random variable, X, is how many hours per night students study for.

\(x \)0123
\(P(X=x)\)0.050.30.50.15

Find \(P\left(2\le X\le3\right)\).

\(P\left(2\le X\le3\right)\) is the probability that a student studies between 2 and 3 hours a night, including those values. That is 0.5 + 0.15 = 0.65.

9

The following table shows the probability distribution of a discrete random variable, A.

a2 345
P(A=a)x0.2 y0.2

Given that E(A) = 3.8, find the value of x and y.

x =

y =

Given that we have two unknowns, we will create 2 simultaneous equations to solve.

Equation 1: \(x+0.2+y+0.2=1\), and thus \(x+y=0.6\)

Equation 2: \(2\times x+3\times 0.2+4 \times y+5\times 0.2=3.8\), and thus \(2x+4y=2.2\)

Solving these linear simultaneous equations on the GDC, we obtain \(x=0.1\) and \(y=0.5\).

10

The following table shows the probability distribution of a discrete random variable, A.

a2 345
P(A=a)0.3xy0.2

Given that E(A) = 3.4, find the value of x and y.

x =

y =

Given that we have two unknowns, we will create 2 simultaneous equations to solve.

Equation 1: \(0.3+x+y+0.2=1\), and thus \(x+y=0.5\)

Equation 2: \(2\times 0.3+3\times x+4 \times y+5\times 0.2=3.4\), and thus \(3x+4y=1.8\)

Solving these linear simultaneous equations on the GDC, we obtain \(x=0.2\) and \(y=0.3\).

 

Central Tendency and Dispersion

1

What is the mean and median of this set of numbers?

8, 5, 6, 9, 2, 5, 3, 6

Mean =

Median =

Use lists and 1 variable data analysis on the GDC

2

What is the the standard deviation of this set of numbers? (Exact or 3.s.f)

42, 63, 62, 59, 48, 33, 41

Standard deviation =

Use lists and 1 variable data analysis on the GDC

3

Work out the mean and the standard deviation of the data from the following frequency table (exact or 3.s.f):

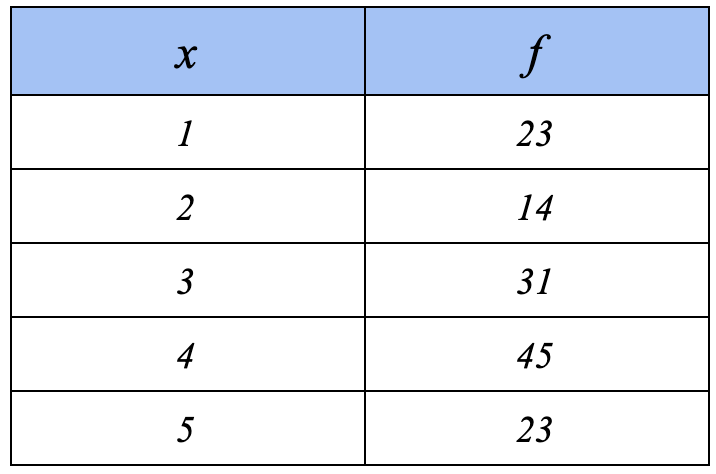
Mean =

Standard deviation =

Use lists and 1 variable data analysis on the GDC - make sure list 2 is set as frequency

4

A set of newborn babies in a hospital were weighed in kilograms. Calculate an estimation of the mean and standard deviation from the data collected in the frequency table below (Exact or 3.s.f)

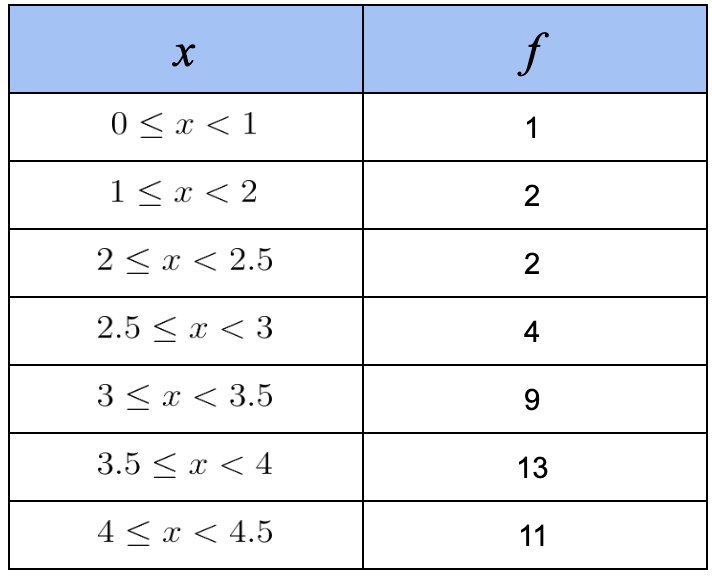
Mean:

Standard deviation:

Use lists and 1 variable data analysis on the GDC - make sure list 2 is set as frequency

To estimate \(x\), calculate the midpoint between the limits

 

Normal Distribution

1

Tick the boxes next to statements you think are true.

If a data set is normally distributed then we would expect it...

2

The ditribution below shows a data set that is normally distributed with a mean of 50 and standard deviation of 10. For each region (labelled A - D) say the percentage of results you would expect to find.

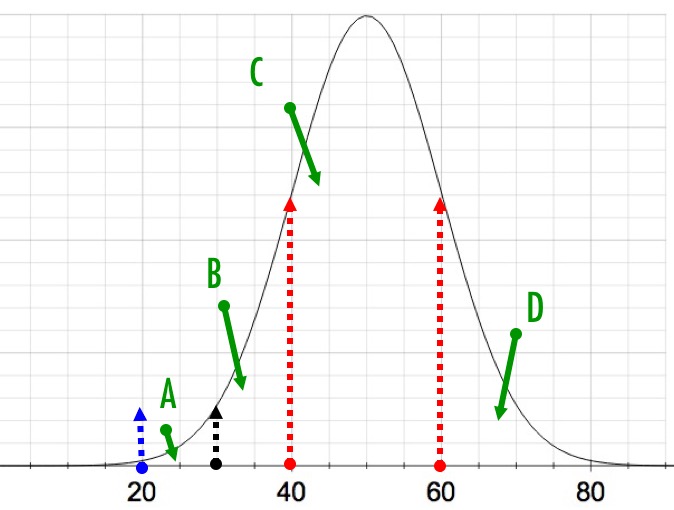
A %, B %, C %, D %

Based on the approximations, 68% +/-1sd, 95% +/-2sd, 99% +/-3sd and the symmetry of the diagram

3

The diagram below shows the normal distribution curve for a data set with a mean of 30 and standard deviation of 5. What pecentage of the data set should be represented by the shaded area.

%

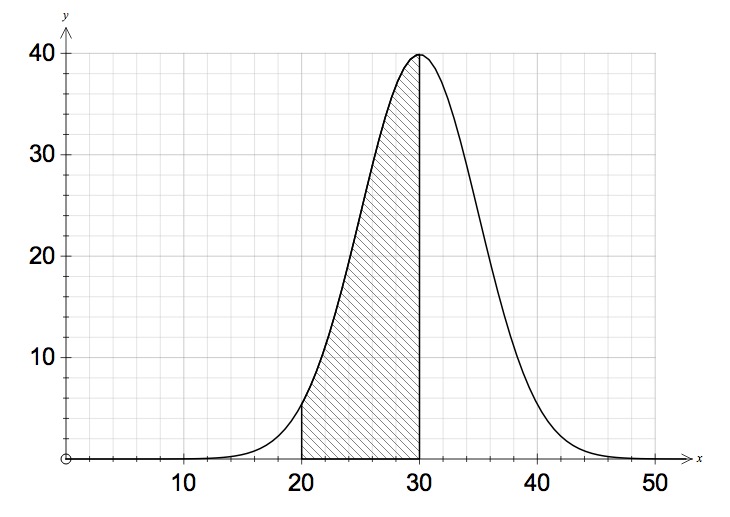
20 is 2 standard deviations below 30. Between 20 and 40 we would expect 95% of the results. As such between 20 and 30 should be half of that.

4

The diagram below shows the normal distribution curve for a data set with a mean of 30 and standard deviation of 5. What pecentage of the data set should be represented by the shaded areas A and B?

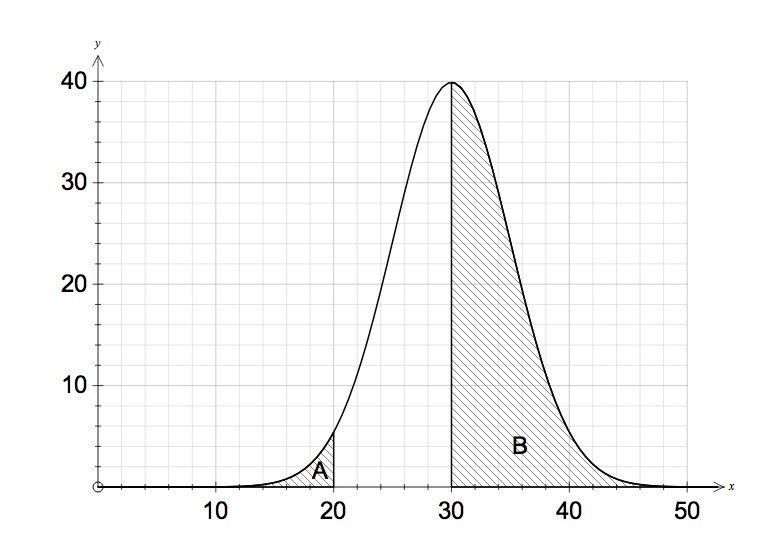
A %, B %

5

Consider a data set that is normally distributed with a mean of 40 and standard devisation of 7. Calculate the probability that a data item selected at random will be in the categories listed below. (give answers correct to 3 sf)

a) Less than 30,

b) Greater than 45,

c) Between 42 and 46,

Enter the Normal CDF function using the Mean, Standard deviation, Lower limit and upper limit.

6

Consider a data set that is normally distributed with a mean of 4.5 and standard devisation of 0.6. Calculate the probability that a data item selected at random will be in the categories listed below. (give answers correct to 3 sf)

a) Less than 3,

b) Greater than 4.7,

c) Between 4 and 6,

Enter the Normal CDF function using the Mean, Standard deviation, Lower limit and upper limit.

7

The weights of a sample of new born babies are normally distributed with a mean of 3.1kg and a standard deviation of 0.8 kg. Find the probability that a baby selected at random from that sample weighed.

a) More than 4kg,

If the sample contained 1500 babies, how many babies would you expect to be more than 4kg?

babies (nearest whole number)

Enter the Normal CDF function using the Mean, Standard deviation, Lower limit and upper limit. Then mutiply the probability by 1500.

8

Consider a data set that is normally distributed with a mean of 40 and standard devisation of 7. The probability of a data item selected at random being less than x, is given by 0.7.

What is the value of x? (3 sf)

Use the inverse normal function with Area/Probability = 0.7, Mean = 40, sd = 7. Round correctly

9

Consider a data set that is normally distributed with a mean of 4.5 and standard devisation of 0.6. The probability of a data item selected at random being more than x, is given by 0.45.

What is the value of x? (3 sf)

Use the inverse normal function with Area/Probability = 0.55, Mean = 40, sd = 7. Probability is 0.55 because that would leave 0.45 to the right. 0.55 is the probability on the left. Round correctly

10

The weights of a sample of new born babies are normally distributed with a mean of 3.1kg and a standard deviation of 0.8 kg. The bottom 10% of the sample were all below x kg.

What is the value of x? (3 sf)

Use the inverse normal function with Area/Probability = 0.1, Mean = 3.1, sd = 0.8. Round correctly

......

 

Probability

1

Question zone

Answers zone

Hidden explanation (optional)

 

Binomial Distribution

1

For \(X\sim B(n,p)\), describe what each element of this probability distribution represents. Use the following statements within the input boxes: discrete random variable, number of trials, probability of success, binomial distribution.

\(X \) is a

\(B\) represents the

\(n\) is the

\(p\) is the

This is clear from the answers above.

2

Given that \(X\sim B(10,0.3)\), find \(P(X=4)\). Give your answer to 1 decimal place.

Using the binomial distribution (pdf) on your GDC, you instantly arrive at the answer 0.2.

3

Given that \(X\sim B(10,0.3)\), find \(P\left(X\le3\right)\). Give your answer to 3 significant figures.

Using the binomial distribution (cdf) on your GDC, ensuring that you input "3" into your calculator as this value must be included, you instantly arrive at the answer 0.6496107..., which is 0.650 written to 3 significant figures.

4

Given that \(X\sim B(8,0.25)\), find \(P\left(X<5\right)\). Give your answer to 3 significant figures.

Using the binomial distribution (cdf) on your GDC, ensuring that you input "4" into your calculator given that "5" is not included, you instantly arrive at the answer 0.97270..., which is 0.973 written to 3 significant figures.

5

There are 20 students in a class. Assuming that being born on any day of the week is equally likely, find the probability that exactly 3 of the students were born on a Monday. Give your answer to 3 significant figures.

This is a binomial distribution, with \(X\) representing the number of students born on a Monday. Hence, \(X\sim B(20,\frac { 1 }{ 7 } )\), since there are 20 students and the probability of being born on a Monday is \(\frac { 1 }{ 7 } \). The question is then, find \(P(X=3)\), which using binomial (pdf) on the GDC, gives 0.242 to 3 significant figures.

6

\(X\sim B(20,0.1)\). Identify which sum below is equivalent to \(P\left(X>18\right)\).

See answer given above.

7

Given that \(X\sim B(8,0.25)\), find \(P\left(X=5\right)\). Give your answer to 3 significant figures.

Use the binomial distribution (pdf) on your GDC, and make sure to round carefully to 3sf

8

Given that \(X\sim B(9,0.3)\), find \(P\left(X\le3\right)\). Give your answer to 3 significant figures.

Using the binomial distribution (cdf) on your GDC, ensuring that you input "3" into your calculator as this value must be included, you instantly arrive at the answer 0.7296..., which is 0.730 written to 3 significant figures.

9

Given that \(X\sim B(10,0.3)\), find \(P(X=3)\). Give your answer to 3sf

Using the binomial distribution (pdf) on your GDC, you instantly arrive at the answer 0.267. See calculator skills page for more help with this!

 
 

Geometry and Trigonometry

Voronoi and Perpendicular Bisectors

1

What is the gradient of the perpendicular bisector of the points (1,1) and (7,3)?

The gradient between the two points is \(\frac{1}{3}\). Hence, the perpendiular gradient is \(-\frac{3}{1}=-3\).

2

Find the equation of the perpendicular bisector between the points (-2, 5) and (4, 3).

Midpoint: \(\left(\frac{-2+4}{2},\frac{5+3}{2}\right)=\left(1,4\right)\)

Gradient: \(\frac{3-5}{4--2}=-\frac{2}{6}=-\frac{1}{3}\)

Perpendicular Gradient: \(\frac{3}{1}=3\)

Equation: \(y=3x+c\)

Substitute \((1,4)\) into the equation: \(4=3\times1+c\), so \(c=1\).

Thus, \(y=3x+1\)

3

Find the equation of the perpendicular bisector between the points given on the graph below.

A vertical line which passes through \(4\) on the x-axis has equation, \(x =4\).

4

A line segment has a gradient of \(3\). What is the gradient of the perpendiular line?

If the gradient is \(3\), we can write the gradient as \(\frac{3}{1}\) so that the perpendicular gradient is \(-\frac{1}{3}\).

5

Below is a Voronoi diagram with an edge missing. Find the equation of the edge, and write your answer in the form \(ax+by+c=0\), where \(a,b,c \in \mathbb{Z}\) and \(a,b>0\).

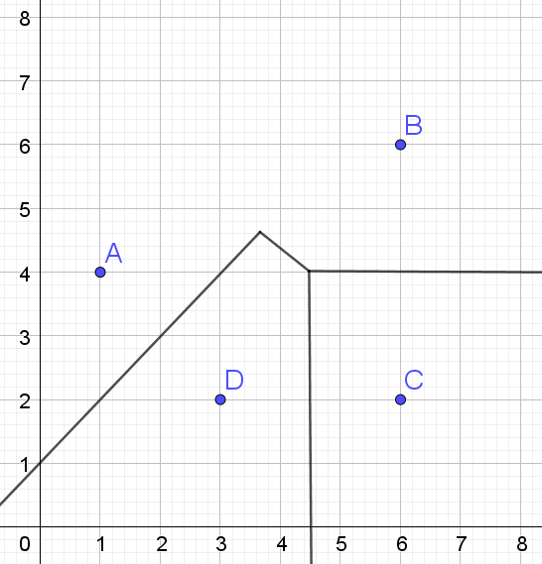
Equation:

The missing edge seperates sites A(1,4) and B(6,6).

Midpoint: \(\left(\frac{1+6}{2},\frac{4+6}{2}\right)=\left(3.5,5\right)\)

Gradient: \(\frac{6-4}{6-1}=\frac{2}{5}\)

Perpendicular Gradient: \(-\frac{5}{2}\)

Equation: \(y=-\frac{5}{2}x+c\)

Substitute \((3.5,5)\) into the equation: \(5=3.5\times-\frac{5}{2}+c\), so \(c=13.75\).

Thus, \(y=-\frac{5}{2}x+13.75\)

Since \(a,b,c \) must be integers with \(a,b>0\), we can multiply te equation by \(4\) and rearrange to obtain

\(10x+4y-55=0\)

6

The rainfall in three nearby cities, A, B, C and D, over the course of the previous month, is 15 cm, 22 cm, 18 cm and 20 cm respectively. Use nearest neighbour interpolation to estimate the rainfall at (2, 3).

cm

The point (2, 3) is located on an edge between the sites C and D. We therefore take the mean of the rainfalls at C and D: \(\frac{18+20}{2}=19\ cm\)

If the point was located inside a cell, then we would estimate the rainfall to be the same as the site within that cell.

7

The rainfall in three nearby cities, A, B, C and D, over the course of the previous month, is 15 cm, 22 cm, 18 cm and 20 cm respectively. Use nearest neighbour interpolation to estimate the rainfall at (5, 3).

cm

The point (5, 3) is located on a vertex between the sites B, C and D. We therefore take the mean of the rainfalls at B, C and D: \(\frac{22+18+20}{3}=20\ cm\)

8

In the Voronoi diagram below, a new site D has been added.

Choose which statement below is the correct process to create a new Voronoi diagram for sites A, B, C and D.

When adding a new site, a perpendicular bistector needs to be found between te new site, and the site which already exists in the cell. Then a new perpendicular bistector must be found between the new site, and any sites in cells which are directly next to the new site.

9

Find the co-ordinates of the missing site in the Voronoi diagram below.

( , )

The missing site is contained in the cell which currently does not have a site.

If we start by looking at the edge between the missing site and site D, it has gradient of 3 right and 1 down, \(-\frac{1}{3}\). Therefore the perpendicular gradient must be \(3\). Utilising the same idea with the edge between site B and the missing site, the gradient is \(-\frac{1}{2}\), which means the perpendicular gradient must be \(2\). Starting at site D and B, and drawing a line backwards with the perpendicular gradients found will ascertain the location of the missing site.

10

Find the centre and radius of the largest empty circle in the Voronoi diagram below.

Since there are two vertices, we will need to check the distance between each vertex and a randomly picked site that each vertex seperates.

For the vertex \((9,5)\), if I randomly pick site A, the distance is given by, \(d=\sqrt{(9-13)^2+(5-4)^2}=\sqrt{(-4)^2+1^2}=\sqrt{17} \)

For the vertex (5, 6), if I randomly pick site D, the distance is given by,

\(d=\sqrt{(5-0)^2+(6-9)^2}=\sqrt{5^2+3^2}=\sqrt{34} \)

Therefore, the largest empty circle has centre \((5, 6)\) and radius \(\sqrt{34} \).

 

Applications of Trigonometry

1

Identify the angle of depression in the figure below:

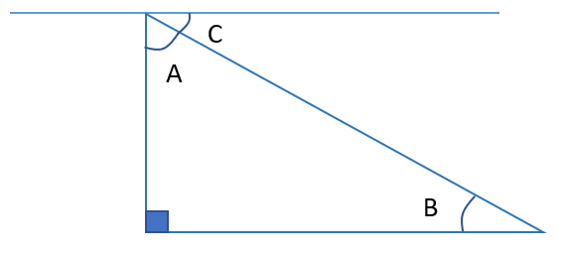
The angle of depression is the angle between the horizontal line of sight and the line of sight down to an object. It is therefore angle C.

2

Find the angle of elevation, \(x\), from the persons head to the top of the tree.

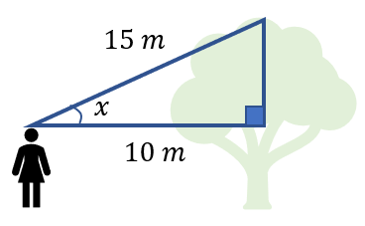
x =

Using right-angle triangle trigonometry, we can find the angle of elevation:

\(cos(\theta)=\frac{10}{15}\)

So, \(\theta=\cos^{-1}\left(\frac{10}{15}\right)\)

\(\theta=48.2^{o}\)

3

A person is standing near a tree. If the angle of elevation is given by 43 degrees, and the person is half the height of the tree, find the height of the tree.

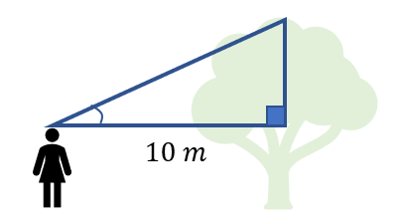
Height of Tree =

First finding the height of the right-angled triangle:

\(\tan\left(43^{o}\right)=\frac{h}{10}\)

\(h=10\cdot\tan\left(43^{o}\right)\)

\(h=9.3251...m\)

Given that the person is half the height of the tree, we can now double the previous answer to obtain the height of the tree.

Height of Tree \(=18.7 \space m\)

4

A lighthouse keeper measures the angle of depression between himself and a ship as \(3^{o}\). If the keeper is 20 metres above the water level, how far is the ship from the lighthouse?

Here is the worded statement translated into a picture:

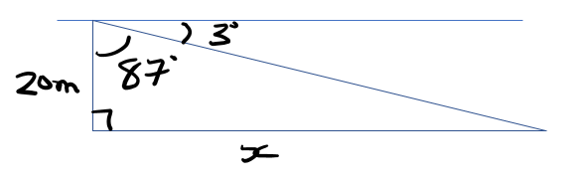
Using right-triangle trigonometry: SOH CAH TOA

\(\tan\left(87\right)=\frac{x}{20}\)

So \(x=20\cdot\tan\left(87\right)\)

\(x= 382 \space{m} (3sf)\)

5

Write the bearing of T from P in each diagram below:

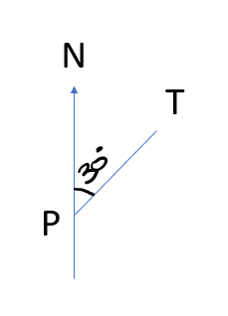
A bearing is a 3-digit angle which is measured clockwise from North. i.e. you start at the North line and identify the angle turned. Therefore, in this case the bearing is \(030^{o}\).

6

Write the bearing of T from P in each diagram below:

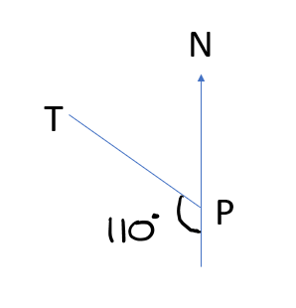
A bearing is a 3-digit angle which is measured clockwise from North. i.e. you start at the North line and identify the angle turned. Therefore, in this case the bearing is \(180^{o}+110^{o}=290^{o}\).

7

The bearing of Ship A to Ship B is \(080^{o}\). Give the bearing of Ship A from Ship B. You do not need to put the degree sign in the textbox provided.

By drawing a sketch, we first see that finding the supplementary angle (\(100^{o}\)) then allows us to calculate the bearing of A from B (or B to A).

8

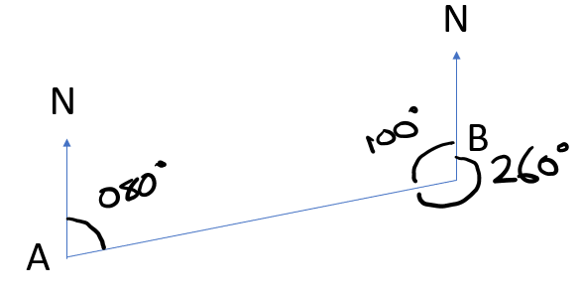
Ships A and B leave port at the same time. Ship A travels at 20 kmh on a bearing of \(045^{o}\) and Ship B travels at 15 kmh on a bearing of \(110^{o}\). How far are the ships away from each other after 3 hours of travelling?

Starting with a sketch:

Once the sketch has been drawn, use the cosine rule to find the missing length.

\(x^{2}=60^{2}+45^{2}-2\cdot60\cdot45\cdot\cos\left(65\right)\)

\(x = 57.8 \space{km}\)

9

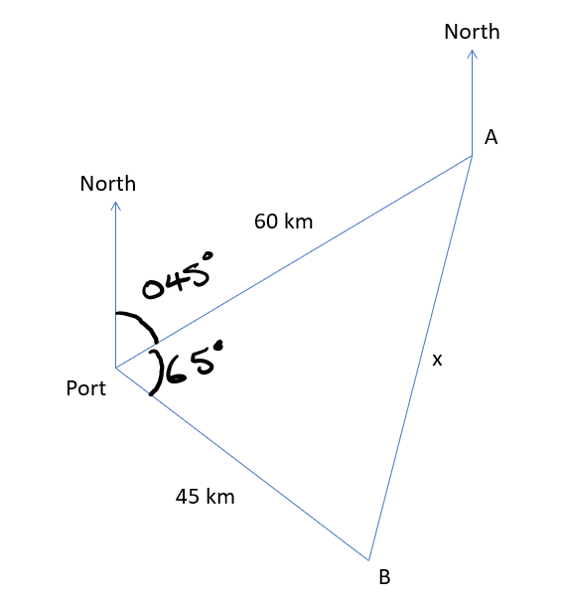
From a lamp post, a skateboarder travels 200 m east before turning on a bearing of \(162^{o}\) for 160 m. She then turns on a bearing of \(242^{o}\) for 380 m, and finally in a straight line back to the original lamp post.

Which of sketches below represent this information?

The bearings in the correct sketch both turn clockwise from North, whereas the second bearing in the incorrect skecth turns anti-clockwise.

10

Find the dotted line distance in the diagram below:

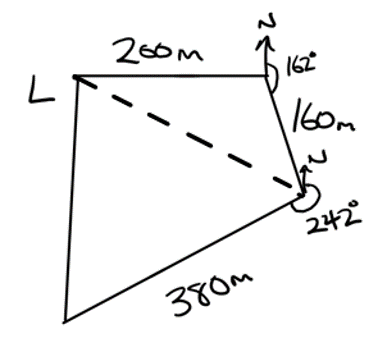
Start by finding the included angle between 200 m and 160 m. This is \(360^{o}-90^{o}-162^{o}=108^{o}\). Then use the cosine rule to find the missing length:

\(x^{2}=200^{2}+160^{2}-2\cdot200\cdot160\cdot\cos\left(108\right)\)

\(x = 292 \space{m}\)

 

Circles

1

Which formula from the formula booklet finds the length of a ciruclar arc, where \(\theta\) is measured in degrees and r is the radius of the arc?

The angle of the arc as a fraction of a whole circle (360 degrees), multiplied by the circumference of a circle (\(2\pi r\)), gives the arc length.

2

Find the length of a cicular arc which has a radius of 5 cm and a central angle of 30°.

Using the arc length formula:

\(l=\frac { 30° }{ 360° } \times 2\times \pi \times 5=2.62\quad cm\)

3

If the area of a sector is \(50{c m }^{ 2 }\) and the central angle is 45 degrees, find the radius of the sector.

Using the formula for the area of a sector:

\(50=\frac { 45° }{ 360° } \times \pi { r }^{ 2 }\)

Dividing both sides by \(\frac { 45° }{ 360° }\) and by \(\pi\):

\({r}^2=127.324...\)

\(\therefore \quad r=11.3cm\)

4

A semi-circlular logo has a radius of 10cm. Find the area of the logo, giving your answer to 1 decimal place.

We could use the formula for the area of a sector, with the angle, \(\theta\), being 180 degrees. However, it may be more efficient to use the formula for the area of a circle and then divide that area by 2 to get the area of the semi-circle.

\(A=\frac { \pi \times { 10 }^{ 2 } }{ 2 } =157.0796{ cm }^{ 2 }=157.1{ cm }^{ 2 }\)

5

Find the arc length of a sector with radius 6cm and a central angle of 120 degrees. Give your answer in terms of \(\pi\).

cm

cm

cm

cm

Using the formula for the arc length of a sector:

\(A=\frac { 120° }{ 360° } \times 2\times \pi \times 6=\frac { 1 }{ 3 } \times 12\pi =\frac { 12\pi }{ 3 } =4\pi \) cm

6

Find the total perimeter of the shape below, giving your answer to 3 significant figures. Do not include units.

There are a number of ways to do this, one way being to find the interior angle of the sector, which is 320°, and then utilize the arc length formula to obtain 39.0954 cm. To then find the total perimeter, we must add 14 cm for the two radii, giving 53.1 cm to 3 significant figures.

7

Find the area of a sector of a circle with radius 8 cm and central angle 10°. Give your answer to 3 significant figures. Do not include units.

The area of the sector is given by:

\(A=\frac { 10° }{ 360° } \times \pi \times { 8 }^{ 2 }=5.5851{ cm }^{ 2 }=5.59{cm}^2\)

8

A garden sprinkler is set at an angle of 160° and a spray distance of 4 metres. Find the area of grass that the sprinkler covers, leaving your answer to 3 significant figures. Do not include units.

Using the area of a sector formula:

\(A=\frac { 160° }{ 360° } \times \pi \times { 4 }^{ 2 }=22.3{ m }^{ 2 }\)

9

Which formulae below find the circumference of a circle, C, with radius, r, and diameter, d?

See answers.

10

The Area of a sector formula is given by, \(A=\frac { \theta }{ 360 } \times \pi { r }^{ 2 }\). Rearrange this formula to write \(\theta\) in terms of \(A\) and \(r\).

Given that \(\theta\) is divided by 360°, we must multiply both sides by 360°. Also, since we are multiplying \(\theta\) by \(\pi{r}^2\), we must divide both sides by \(\pi{r}^2\). Essentially we are conducting the inverse operations when rearranging.

 

Volume and Surface Area

1

a) What is the volume of the cuboid in the diagram below?

b) What is its surface area?

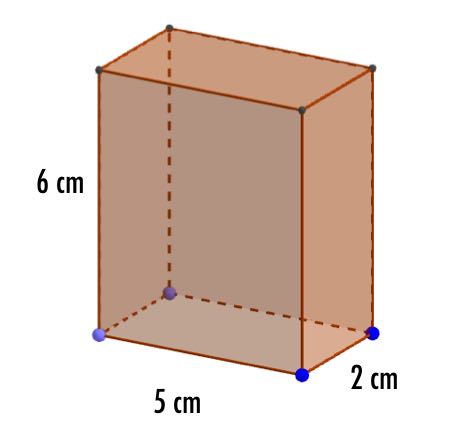
Write a number only

a) Volume = cm3

b) Surface area = cm2

The volume of the base is 5 x 2, then multiply by the height, 6, giveives volume = 5 x 2 x 6

b) 2 faces are 5 x 2, 2 faces are 6 x 2 and 2 faces are 5 x 6, giving a total of 20 + 24 + 60 = 104cm2

....

2

Drag the correct name of the shape in to the right box.

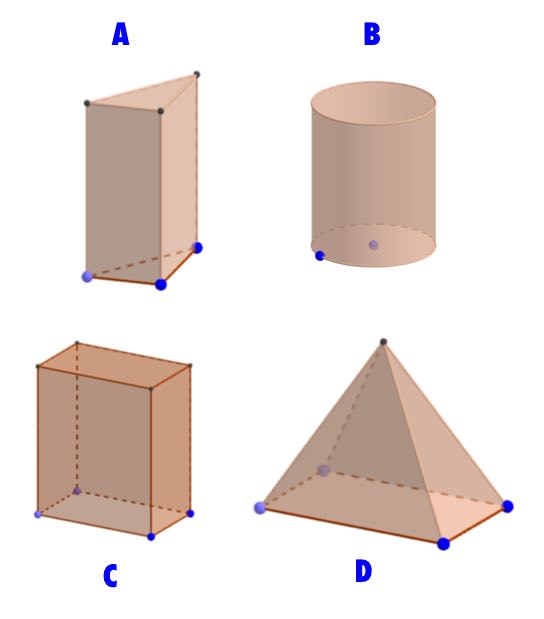
Shape A Triangular prism Pyramid
Shape B Cylinder Cone
Shape C Cuboid Octangonal based pyramid
Shape D  
Rectangular based Pyramid Sphere
 

....

3

The following right angled triangle is one face of a triangular prism whose length is 12 cm....

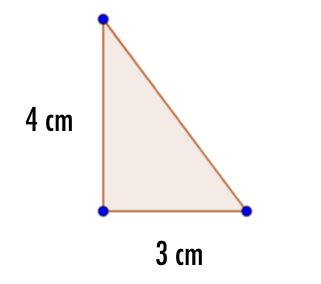
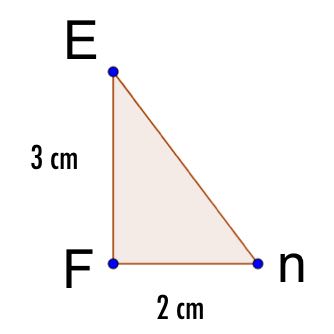
a) Calculate the length of the hypotenuse of the triangle

b) What is the area of the triangular cross section?

c) What is the volume of the prism?

d) What is the total surface area of the prism?

 

Write numbers only

a) Length of hypotenuse is cm

b) The area of the triangular cross section is cm2

c) The volume of the prism is cm3

d)The total surface area of the prism is cm2

a) Using pythagoras theorem, h2 = 32 + 42

b) Area = (3 x 4)/2 = 6

c) Volume is corss sectional area x length, so V = 6 x 12 = 72

d) There are 5 faces, 2 triangles on each end each 6, the bottom which is 3 x 12, the back which is 4 x 12 and the sloping face which is 5 x 12, so 6 + 6 + 36 + 48 + 60 = 156

....

4

A triangular prism has a volume of 300 cm3 and a length of 15cm.

a) What is the area of the triangular cross section?

b) If the triangular corss section has a height of 5cm, how long is its base?

a) Area of triangular face is cm2

b) the base of the triangular criss section is cm

a) Volume = Cross section x length, so 300 = Cross section x 15. Cross section = 300/15

b) Area of truiangle is base x height / 2. If base x 5/2 = 20 then base must be 8

...

5

Consider the following cylinder with a radius of 7 cm and a heigth of 15 cm

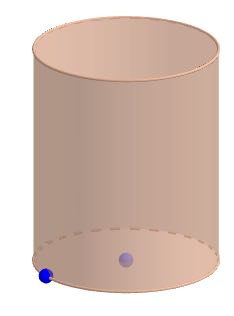
a) Work out the volume of the cylinder

b) Work out the surface are of the cylinder

Give your answers to 3sf

a) Volume = cm3

b) Surface area = cm2

a) Volume of a cylinder = (pi)r2h. in this case pi x 72 x 15 = 2039.07060 which is 2040 to 3sf

b) Surface area of a cylinder = 2 (pi)r2 + 2(pi)rh, substitute r = 7 and h = 15 and you get SA = 4926.01728 which rounds to 4930 to 3sf

....

6

Consider the following rectangular based Pyramid and its net. CD = 4cm, BC = 2cm, EF = 3cm

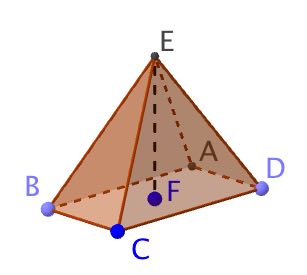
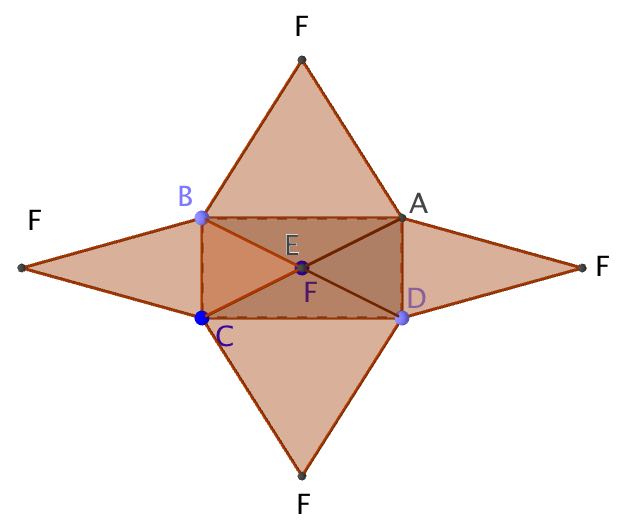
a) Work out the volume of the pyramid

b) What is the perpendicualr height, h, of triangle ECD? (give answer to 3sf)

c) What is the perpendicualr height, p, of triangle EBC? (give answer to 3sf)

d) Calculate the surface area of the Pyramid using rounded answers to the previous questions

a) V = cm3

b) h = cm

c) p = cm

d) SA = cm2

a) \(V=\frac { 1 }{ 3 } Area\quad of\quad base\quad \times \quad heigth\\ V\quad =\quad \frac { 2\times 4\times 3 }{ 3 } =8{ cm }^{ 3 }\)

b) Consider m to be the midpoint of CD then we have the folllowing triangle

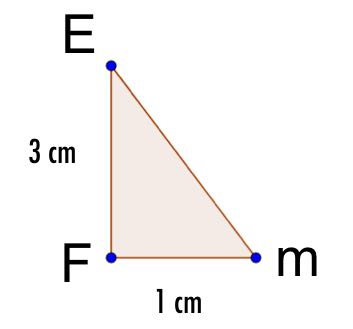The vertical height of triangle ECD is

\(h\quad =\quad \sqrt { { 3 }^{ 2 }+{ 1 }^{ 2 } } \\ h\quad =\quad 3.162277\\ h\quad =\quad 3.16\quad cm\quad (3sf)\)

c) Consider n to be the midpoint of BC then we have the folllowing triangle

The vertical height of triangle EBC is

\(p\quad =\quad \sqrt { { 3 }^{ 2 }+{ 2 }^{ 2 } } \\ p\quad =\quad 3.605551\\ p\quad =\quad 3.61\quad cm\quad (3sf)\)

d) \(Base\quad area\quad =\quad 2\quad x\quad 4\quad =\quad 8{ cm }^{ 2 }\\ \\ Triangle\quad ECD\quad =\quad triangle\quad EBA\quad \\ Area\quad =\quad \frac { 3.16\times 4 }{ 2 } =\quad 6.32\\ \\ Triangle\quad EBC\quad =\quad triangle\quad EAD\quad \\ Area\quad =\quad \frac { 3.61\times 2 }{ 2 } =\quad 3.61\\ \\ Total\quad surface\quad area\quad =\quad 8\quad +\quad 2\times 6.32\quad +\quad 2\times 3.61\quad =\quad 27.86\quad { cm }^{ 2 }\quad \\ \\ \)

SA = 27.9 (3sf)

...

7

Calculate a) the volume and b) the surface area of a cone with a base radius of 5cm and a height 12cm

a) Volume = cm3

b) Surface area = cm2

a) \(Volume\quad of\quad a\quad cone\quad =\quad \frac { \pi { r }^{ 2 }h }{ 3 } \\ V\quad =\quad \frac { \pi { \quad \times \quad 5 }^{ 2 }\quad \times \quad 12 }{ 3 } \\ V\quad =\quad 314.15926\\ V\quad =\quad 314\quad { cm }^{ 3 }\\ \\ \)

b)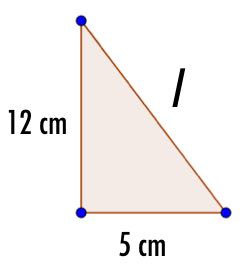 The profile of the cone looks like the diagram to the left. the slant height, l is calculated....

\(Slant\quad height\quad of\quad a\quad cone,\quad l\\ l\quad =\quad \sqrt { { 5 }^{ 2 }+{ 12 }^{ 2 } } \\ l\quad =\quad \sqrt { 169 } \\ l\quad =\quad 13\quad cm\\ \\ \\ \)

\(Surface\quad area\quad of\quad a\quad cone\quad =\quad \pi { r }^{ 2 }+\pi rl\\ SA\quad =\quad \pi \quad \times \quad 25\quad +\quad \pi \quad \times \quad 5\quad \times \quad 13\\ SA\quad =\quad 282.7433\\ SA\quad =\quad 283\quad { cm }^{ 2 }\)

8

The right angled triangle on the left is the base of a right pyramid whose volume is 90 cm3. What is the height of the pyramid?

Height = cm

\(Volume\quad of\quad pyramid\quad =\quad \frac { 1 }{ 3 } Area\quad of\quad base\quad \times \quad height\quad \\ 90\quad =\quad \frac { 1 }{ 3 } \quad \times \quad 6\quad \times \quad h\\ 270\quad =\quad 6h\\ h\quad =\quad \frac { 270 }{ 6 } \quad =\quad 45cm\\ \\ \\ \)

9

What is a) the volume and b) the surface area of a Sphere with a radius of 10cm? Give answers to 3sf

a) Volume = cm3

b) Surface Area = cm2

a) \(Volume\quad of\quad sphere\quad =\quad \frac { 4 }{ 3 } \pi { r }^{ 3 }\\ V\quad =\quad \frac { 4 }{ 3 } \pi \quad \times \quad 10^{ 3 }\\ V\quad =\quad 4188.7902\\ V\quad =\quad 4190\quad { cm }^{ 3 }\quad (3sf)\\ \\ \\ \)

b) \(Surface\quad Area\quad of\quad sphere\quad =\quad 4\pi { r }^{ 2 }\\ SA\quad =\quad 4\pi { \quad \times \quad 10 }^{ 2 }\\ SA\quad =\quad 1256.6370\\ SA\quad =\quad 1260\quad { cm }^{ 2 }\quad (3sf)\\ \\ \\ \)

10

A sphere and a cone have the same radius, 7cm, and the same volume. What is the height of the cone? Do not round until your final answer then give your answer to 3sf.

Height of cone = cm

\(Volume\quad of\quad sphere\quad =\quad \frac { 4 }{ 3 } \pi { r }^{ 3 }\\ { V }_{ sphere }\quad =\quad \frac { 4 }{ 3 } \pi \quad \times \quad 7^{ 3 }\\ { V }_{ sphere }\quad =\quad 1436.7550402\quad (Keep\quad calculator\quad display)\\ \\ { V }_{ sphere }\quad =\quad { V }_{ cone\quad }=\quad \frac { 1 }{ 3 } \pi { r }^{ 2 }h\quad =\quad \frac { 1 }{ 3 } \pi { \quad \times \quad 7 }^{ 2 }h\\ (\times 3)\quad \quad \quad 3\quad \times \quad { V }_{ sphere }\quad =\quad \pi { \quad \times \quad 49 }h\\ (\div 49\pi )\quad \frac { 3\quad \times \quad { V }_{ sphere } }{ 49\pi } \quad =\quad h\\ h\quad =\quad 27.99999999\\ h\quad =\quad 28.0\quad cm\quad (3sf)\\ \\ \)

 

Right Angled Trigonometry

1

Use your calculator to work out solve the following equations. Give your answers as decimals correct to 3sf.

a) x = sin 35

b) y = tan 75

c) z = cos 26

d) Sinp = 0.7

e) Cosq = 0.1

f) Tanr = 2.5

a) x =

b) y =

c) z =

d) p =

e) q =

f) r =

This is really just about correctly using the buttons on your calculator. For the last three parts when you have the sine of an angle, you need the inverse sine of that number to get the angle. For example,

part d) \(sin\quad p\quad =\quad 0.7\\ so\quad p\quad =\quad { sin }^{ -1 }(0.7)\quad =\quad 44.4\\ \\ \)

2

Use your calculator to work out solve the following equations. Give your answers as decimals correct to 3sf

a) \(sin\quad 30\quad =\quad \frac { x }{ 10 } \) , so x =

b) \(Cos\quad 40\quad =\quad \frac { 5 }{ x } \) , so x

c) \(Tan\quad x\quad =\quad \frac { 7 }{ 14 } \), so x =

a) \(sin\quad 30\quad =\quad \frac { x }{ 10 } \\ so\quad x\quad =\quad 10\quad \times \quad sin\quad 30\quad =\quad 5.00\)

b) \(Cos\quad 40\quad =\quad \frac { 5 }{ x } \\ so\quad x\quad =\quad \frac { 5 }{ cos\quad 40 } =\quad 6.53\)

c) \(Tan\quad x\quad =\quad \frac { 7 }{ 14 } \\ so\quad x\quad =\quad { tan }^{ -1 }\left( \frac { 7 }{ 14 } \right) =\quad 26.6\)

3

Consider the folloiwng diagram

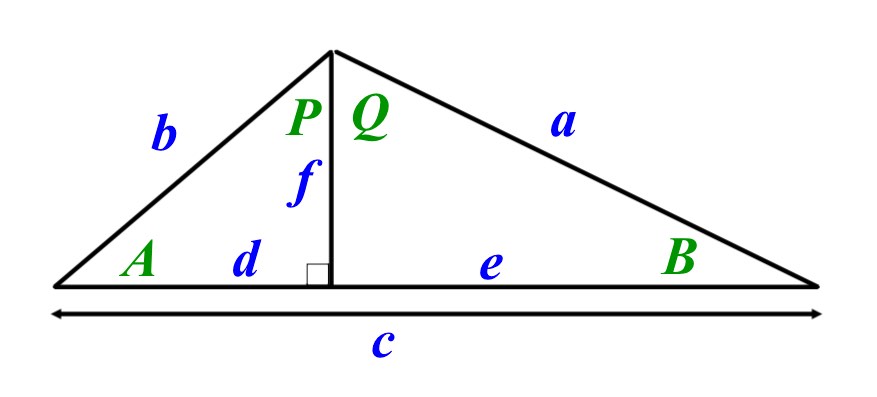
Capital letters (in green) are angles. Lower case letters (in blue) are side lengths.

Next to each of the statements below, enter either 'T' for True of 'F' for False

  1. \(Sin\quad A\quad =\quad \frac { f }{ b } \)
  2. \(Cos\quad B\quad =\quad \frac { f }{ a } \)
  3. \(Tan\quad P\quad =\quad \frac { f }{ d } \)
  4. \(Cos\quad Q\quad =\quad \frac { e }{ a } \)
  5. \(Tan\quad B\quad =\quad \frac { f }{ e } \)
  6. \(Sin\quad Q\quad =\quad \frac { e }{ a } \)
  7. \(Sin\quad A\quad =\quad Cos\quad P\)
  8. \(Tan\quad A\quad =\quad Tan\quad B\)

This question is really about encouraging the making of statements that are true about a given situation. In practice you can then pick which ones will be mist hepful to you. Clearly it depends on remmebering the trig ratios - SOHCAHTOA and identifying the Hypotenuse as the longest side and the positions of the Opposite and adject sides relative to the angle in question.

4

Consider the triangle in the image below.

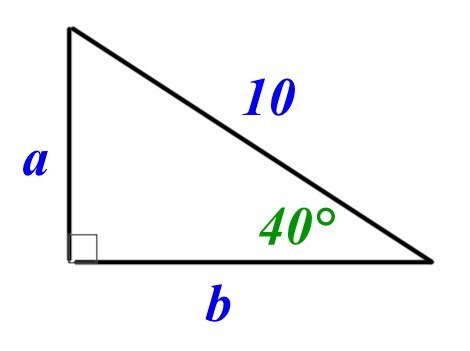
Use trigonometry to work out the lengths of sides a and b in the diagram. Give your answer correct to 3 sf.

a =

b =

a, \(Sin40\quad =\quad \frac { a }{ 10 } \\ so\quad a\quad =\quad 10\times sin40\\ a\quad =\quad 6.43\quad (3sf)\)

b, \(Cos40\quad =\quad \frac { b }{ 10 } \\ so\quad b\quad =\quad 10\times cos40\\ a\quad =\quad 7.66\quad (3sf)\)

5

Consider the triangle in the image below.

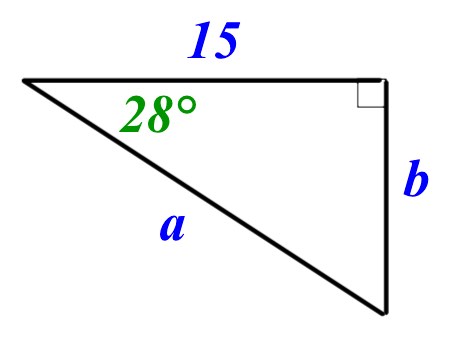
Use trigonometry to work out the lengths of sides a and b in the diagram. Give your answer correct to 3 sf.

a =

b =

a, \(sin28\quad =\quad \frac { 15 }{ a } \\ so\quad a\quad =\quad \frac { 15 }{ sin28 } \\ a\quad =\quad 32.0\quad (3sf)\)

b, \(tan28\quad =\quad \frac { b }{ 15 } \\ so\quad b\quad =\quad 15\times tan28\\ a\quad =\quad 7.98\quad (3sf)\)

6

Consider the triangle in the image below.

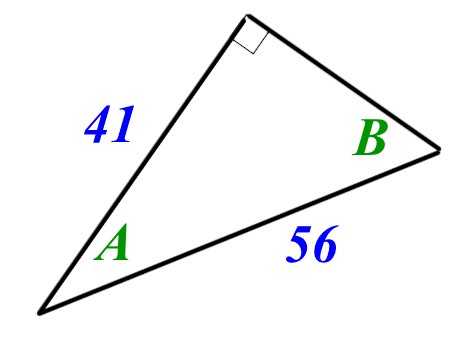
Use trigonometry to work out the lengths of angles A and B in the diagram. Give your answer correct to 3 sf.

A =

B =

A, \(cos\quad A\quad =\quad \frac { 41 }{ 56 } \\ so,\quad A\quad =\quad { cos }^{ -1 }\left( \frac { 41 }{ 56 } \right) \\ A\quad =\quad 42.9\quad (3sf)\)

B, \(sin\quad B\quad =\quad \frac { 41 }{ 56 } \\ so,\quad B\quad =\quad { sin }^{ -1 }\left( \frac { 41 }{ 56 } \right) \\ A\quad =\quad 47.1\quad (3sf)\)

NOTE, A + B = 90 as they should!

7

The diagram below shows a ladder put against a house for cleaning the gutters. The yop of the ladder is 5m above the ground and the angle the ladder makes with the horizontal must be 65°.

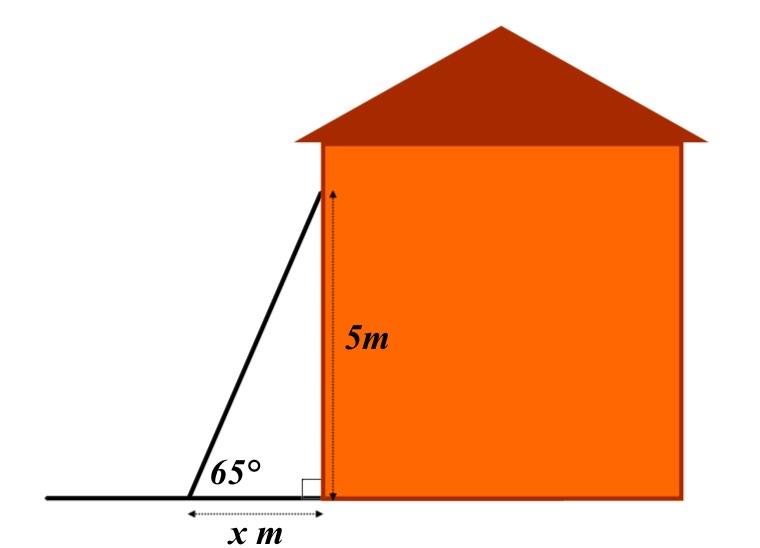
a) How far away (x) from the wall must the base of the ladder be put to make the angle 65°

b) How long does the ladder need to be? (Use trigonometry and unrounded numbers to answer this question)

c) If the length of the ladder is fixed at 6m and the height against the house remains at 5m, what would the angle between the ladder and the gorund become?

d) What is the precentage error in the new angle from the required 65°? (Use the rounded answer to part c)

a) x = m

b) length of ladder = m

c) New angle betwen the ladder and the ground = °

d) Percentage error = %

a) \(tan\quad 65\quad =\quad \frac { 5 }{ x } \\ so,\quad x\quad =\quad \frac { 5 }{ tan\quad 65 } \\ A\quad =\quad 2.33\quad (3sf)\)

b) \(sin\quad 65\quad =\quad \frac { 5 }{ l } \\ so,\quad l\quad =\quad \frac { 5 }{ sin\quad 65 } \\ A\quad =\quad 5.52\quad (3sf)\\ \\ OR\quad { l }^{ 2 }\quad =\quad { 5 }^{ 2 }+{ x }^{ 2 }\\ Using\quad the\quad unrounded\quad answer\quad for\quad x\quad gives\quad the\quad same\quad result\quad for\quad l\)

NOTE, you could have used cosine with x and 65°. Again if you used the unrounded anser for x you would have got the same result.

c) 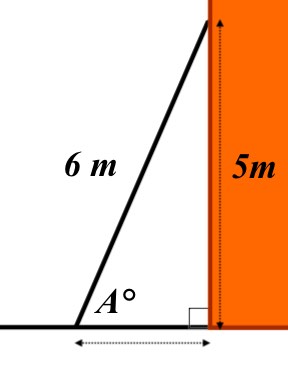\(sin\quad A\quad =\quad \frac { 5 }{ 6 } \\ so,\quad A\quad =\quad { sin }^{ -1 }\left( \frac { 5 }{ 6 } \right) \\ A\quad =\quad 56.4\quad (3sf)\)

d) = \(\frac { 65\quad -\quad 56.4 }{ 65 } \times \quad 100\quad =\quad 13.2\)

8

The diagram below shows part of a metal structure and lists some its geometrical properties.

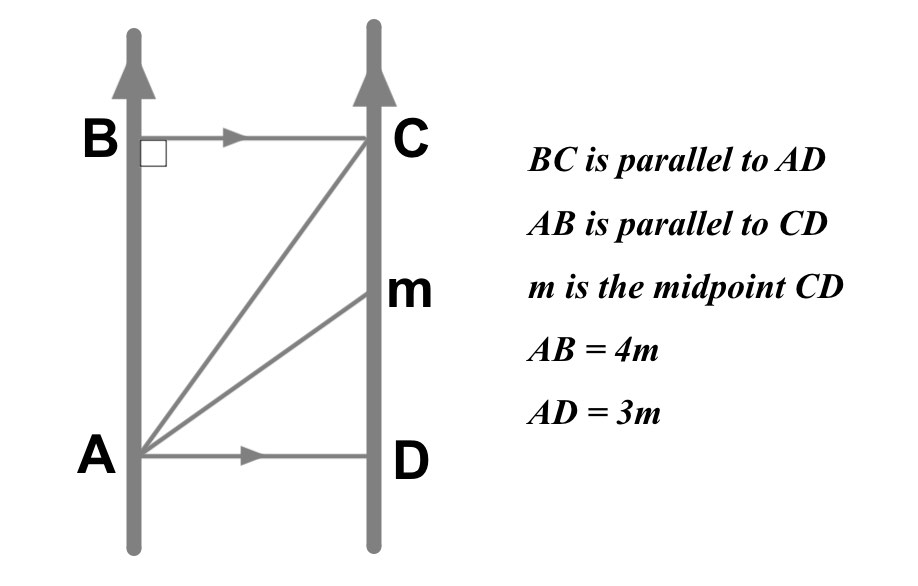
Find the folllowing giving all answers correct to 3sf

a) The length AC = m

b) \(\hat { CAD } \) = °

c) \(\hat { mAD } \) =

In changes to the design it is decided that \(\hat { mAD } \) needs to be exactly halved

d) What is the new length AM? m

a) \({ AC }^{ 2 }\quad =\quad { 4 }^{ 2 }+{ 5 }^{ 2 }\\ AC\quad =\sqrt { 25 } =5.00\quad (3sf)\)

b) \(tan\hat { CAD } =\frac { 4 }{ 3 } \\ so,\quad \hat { CAD } \quad =\quad { tan }^{ -1 }\left( \frac { 4 }{ 3 } \right) \\ \hat { CAD } \quad =\quad 53.1°\)

c) \(tan\hat { mAD } =\frac { 2 }{ 3 } \\ so,\quad \hat { mAD } \quad =\quad { tan }^{ -1 }\left( \frac { 2 }{ 3 } \right) \\ \hat { mAD } \quad =\quad 45.0°\)

d) 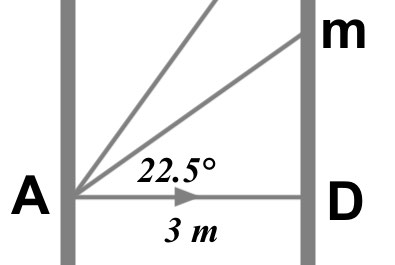\(cos22.5\quad =\quad \frac { 3 }{ mA } \\ so,\quad mA\quad =\quad \frac { 3 }{ cos\quad 22.5 } \\ mA\quad =\quad 3.25m\quad (3sf)\)

9

USe the diagram below for the following questions.

The angle of elevation from Point A to some looking out of the window at point B is 60°

a) What is the height, h, of point B above the ground?

A person looking at point A from point C is 35m above the ground.

b) What is the angle of depression, D, they are looking at?

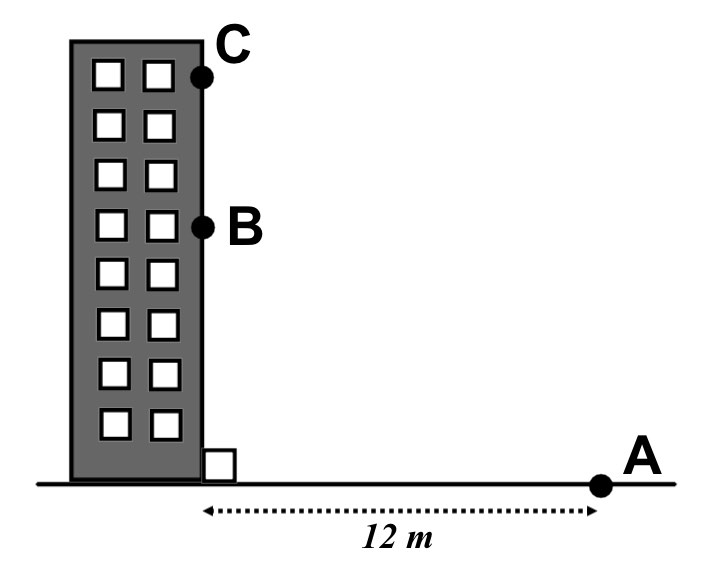
a) Height h =

b) Angle of depression, a =

a) 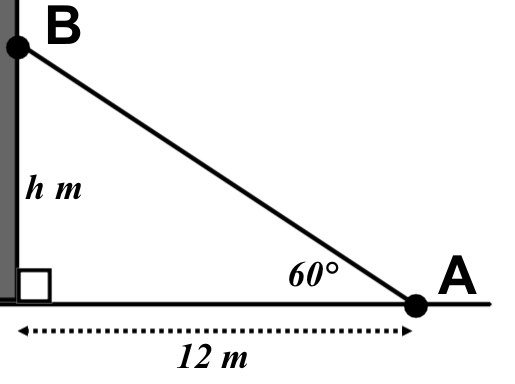\(tan60\quad =\quad \frac { h }{ 12 } \\ so,\quad h\quad =\quad 12\times tan60\\ h\quad =\quad 20.9m\quad (3sf)\)

b) 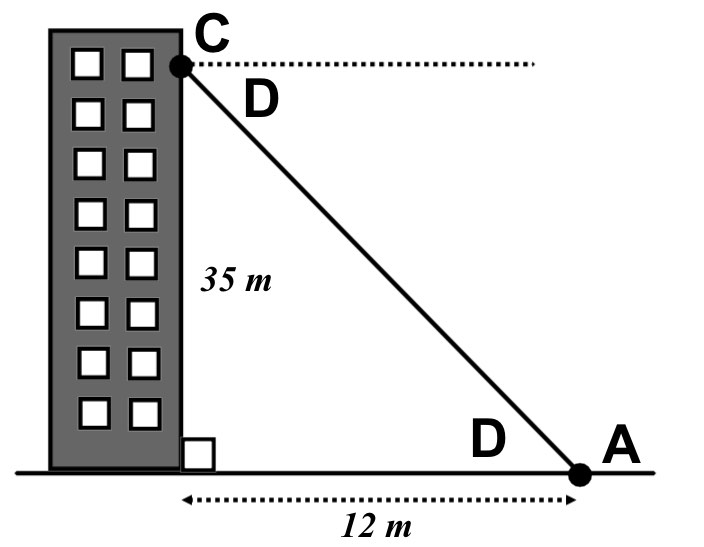\(tanD\quad =\quad \frac { 35 }{ 12 } \\ so,\quad D\quad =\quad { tan }^{ -1 }\left( \frac { 35 }{ 12 } \right) \\ h\quad =\quad 71.1°\quad (3sf)\)

10

The diagram below shows ta narrow chanel of water between the cliff coasts of two islands. Some distances are shown.

The diagram also shows.....

  • The top of a lighthouse at point A
  • The view from the base of the light house at point B
  • A boat at point C
  • The view from the top of the cliff at point D

The angle of elevation of point D from point C is 65°. The angle of depression of point C from point D is 40°.

a) Find the width of the water chanel by finding the respective distances x and y to 3sf. (Use rounded answers to get the total width)

The angle of elevation from point C to point A is 75° .

b) What is the height of the lighthouse above the the ground? (Use rounded ansers to any distances you have calculated)

c) What is the angle, p, of depression from the top of the light house to point D? (Use rounded ansers to any distances you have calculated)

a) x = m to (3sf), y = m (3sf),

Total distance = m

b) h = m

a) \(tan40\quad =\quad \frac { 10 }{ x } \\ x\quad =\quad \frac { 10 }{ tan40 } \\ x\quad =\quad 11.9\quad (3sf)\)

\(tan65\quad =\quad \frac { 18 }{ y } \\ y\quad =\quad \frac { 18 }{ tan65 } \\ y\quad =\quad 8.39\quad (3sf)\)

Total distance = 8.39 + 11.9 = 20.29 , 20.3 (3sf)

b) 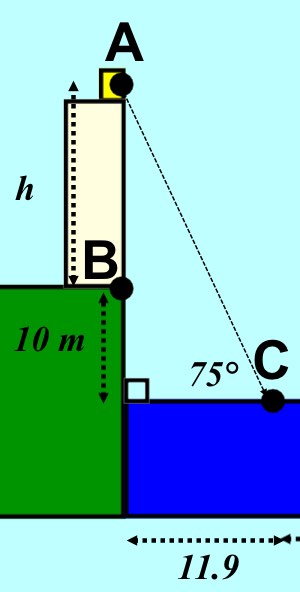\(tan75\quad =\quad \frac { h+10 }{ 11.9 } \\ h\quad +\quad 10\quad =\quad 11.9\times tan75\\ h\quad =\quad 11.9\times tan75\quad -\quad 10\\ h\quad =\quad 34.4\quad m\quad (3sf)\)

c) \(tanp\quad =\quad \frac { 10\quad +\quad 34.4\quad -\quad 18 }{ 11.9 } =\frac { 26.4 }{ 20.3 } \\ p\quad =\quad { tan }^{ -1 }\left( \frac { 26.4 }{ 20.3 } \right) \\ p\quad =\quad 52.4\quad (3sf)\)

 

Non Right Angled Trigonometry

1

Solve the following equations, giving your answers correct to 3sf

a) \(\frac { a }{ Sin20 } =\frac { 10 }{ sin30 } \) b) \(\frac { 18 }{ sinA } =\frac { 27 }{ sin40 } \) c) \({ a }^{ 2 }={ 7 }^{ 2 }+{ 10 }^{ 2 }-2\times 7\times 10\times cos48\) d) \(cosA\quad =\quad \frac { { 13 }^{ 2 }+{ 20 }^{ 2 }-{ 8 }^{ 2 } }{ 2\times 13\times 20 } \)

a) a = b) b = °

c) a = d) A = °

a) \(\frac { a }{ sin20 } =\frac { 10 }{ sin30 } \\ a\quad =\quad \frac { 10 }{ sin30 } \times sin20\\ a\quad =\quad 6.84\quad (3sf)\)

b) \(\frac { 18 }{ sinA } =\frac { 27 }{ sin40 } \\ \frac { sinA }{ 18 } =\frac { sin40 }{ 27 } \\ sinA\quad =\quad \frac { sin40 }{ 27 } \times 18\\ A\quad =\quad { sin }^{ -1 }\left( \frac { sin40 }{ 27 } \times 18 \right) \\ A\quad =\quad 25.4°\quad (3sf)\)

c) \({ a }^{ 2 }={ 7 }^{ 2 }+{ 10 }^{ 2 }-2\times 7\times 10\times cos\quad 48\\ a=\sqrt { 149\quad -\quad 140cos48 } \\ a\quad =\quad 7.44\quad (3sf)\)

d) \(cosA\quad =\quad \frac { { 13 }^{ 2 }+{ 20 }^{ 2 }-{ 8 }^{ 2 } }{ 2\times 13\times 20 } \\ A\quad =\quad { cos }^{ -1 }\left( \frac { { 13 }^{ 2 }+{ 20 }^{ 2 }-{ 8 }^{ 2 } }{ 2\times 13\times 20 } \right) \\ A\quad =\quad 13.8° (3sf)\)

2

Consider the following diagram

Mark each of the following statements about the diagram as either true (T) or false (F)

Enter either 'T' for true or 'F' for false

a) \(\frac { sinA }{ a } =\frac { sinB }{ b } \)

b) \({ b }^{ 2 }={ a }^{ 2 }+{ c }^{ 2 }-2ac\times cosQ\)

c) \(cosB\quad =\quad \frac { { a }^{ 2 }+{ c }^{ 2 }-{ b }^{ 2 } }{ 2ac } \)

d) \(\frac { c }{ sin(P+Q) } =\frac { a }{ sinA } \)

a) T - Angles and sides in each fraction are opposite eachother

b) F - Q is not the angle between sides a and c

c) T - B is the angle between a and c

d) T - P + Q is the angle opposite side c and likewise for A and a

3

Consider the diagram below.

a) What is the exact value of z?

b) Find the values of x and y (give your answer to 3sf)

z = °

x = cm

y = cm

a) Since angles in a triangle add up to 180°, z = 100

b) \(\frac { x }{ sin50 } =\frac { 10 }{ sin30 } \\ x\quad =\quad \frac { 10 }{ sin30 } \times sin50\\ x\quad =\quad 15.3\quad cm\quad (3sf)\)

c) \(\frac { y }{ sin100 } =\frac { 10 }{ sin30 } \\ y\quad =\quad \frac { 10 }{ sin30 } \times sin100\\ y\quad =\quad 19.7\quad cm\quad (3sf)\)

4

For the triangle below

a) Calculate the value of z to 3sf

b) Use that rounded value for z and the sine rule to work out the value of x

c) Again, use the rounded value of z to calculate the area of the triangle

a) z = ° , b) x = m, c) Area = \({ cm }^{ 2 }\)

a) \(\frac { sinz }{ 57 } =\frac { sin44 }{ 43 } \\ sinz\quad =\quad \frac { sin44 }{ 43 } \times 57\\ z\quad =\quad { sin }^{ -1 }\left( \frac { sin44 }{ 43 } \times 57 \right) \\ z\quad =\quad 67.0°\quad (3sf)\)

b) Since z = 67.0° to 3sf, we can calculate that the thrid angle (opposite side x) is 23°

\(\frac { x }{ sin23 } =\frac { 43 }{ sin44 } \\ x\quad =\quad \frac { 43 }{ sin44 } \times sin23\\ y\quad =\quad 24.2\quad cm\quad (3sf)\)

c) \(Area\quad =\quad \frac { 1 }{ 2 } \times 43\times 57\times sin23\\ Area\quad =\quad 479{ cm }^{ 2 }\)

5

Consider the following diagram

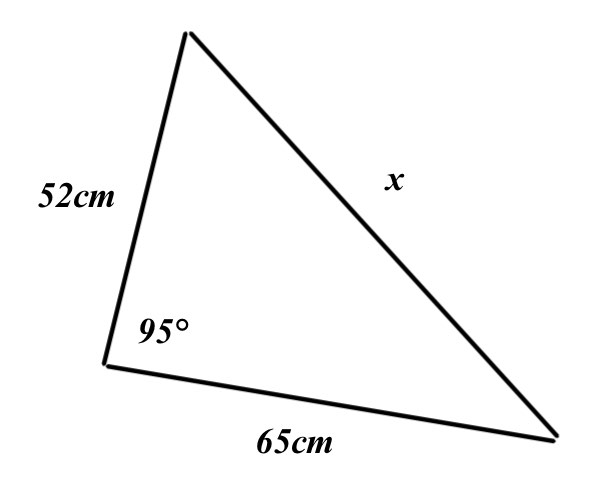
a) Work out the value of x

b) Work out the area of the triangle

a) x = cm

b) Area = \({ cm }^{ 2 }\)

a) \({ x }^{ 2 }={ 52 }^{ 2 }+{ 65 }^{ 2 }-2\times 52\times 65\times cos95\\ a=\sqrt { 6929\quad -\quad 3380cos95 } \\ a\quad =\quad 85.0cm\quad (3sf)\)

b) \(Area\quad =\quad \frac { 1 }{ 2 } \times 52\times 65\times sin95\\ Area\quad =\quad 1683.56904\\ Area\quad =\quad 1680\quad { cm }^{ 2 }\quad (3sf)\)

6

Answer questions referring to the diagram below.

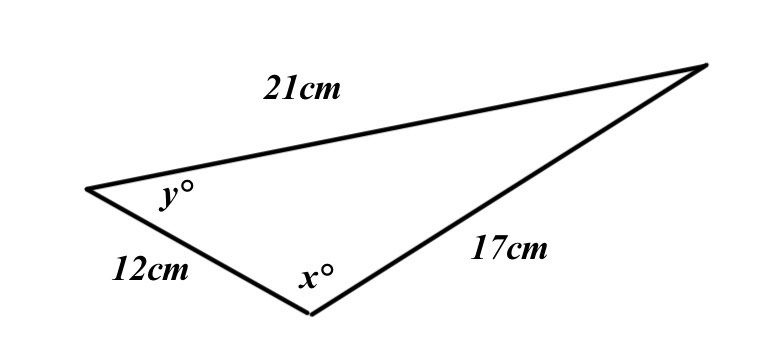
a) Calculate the value of x to 3sf.

b) Calculate the value of y to 3sf.

c) Use the rounded value of x to work out the area of the triangle

a) x = °

b) y = °

c) Area = \({ cm }^{ 2 }\)

a) \(cosx\quad =\quad \frac { { 12 }^{ 2 }+{ 17 }^{ 2 }-{ 21 }^{ 2 } }{ 2\times 12\times 17 } \\ x\quad =\quad { cos }^{ -1 }\left( \frac { { 12 }^{ 2 }+{ 17 }^{ 2 }-{ 21 }^{ 2 } }{ 2\times 12\times 17 } \right) \\ x\quad =\quad 91.1°\)

b) \(cosy\quad =\quad \frac { { 12 }^{ 2 }+{ 21 }^{ 2 }-{ 17 }^{ 2 } }{ 2\times 12\times 21 } \\ y\quad =\quad { cos }^{ -1 }\left( \frac { { 12 }^{ 2 }+{ 21 }^{ 2 }-{ 17 }^{ 2 } }{ 2\times 12\times 21 } \right) \\ y\quad =\quad 54.0°\)

c) \(Area\quad =\quad \frac { 1 }{ 2 } \times 12\times 17\times sin91.1\\ Area\quad =\quad 101.9812026\\ Area\quad =\quad 102\quad { cm }^{ 2 }\quad (3sf)\)

7

Consider the square based pyramid ABCDE

EF = 4cm, GF = 3cm, CD = 6cm, EC = \(\sqrt { 34 } cm\)

a) What is the angle \(\hat { DEC } \) (to 3sf)

b) What is the angle, y, between FG and the plane ECD

c) What is the angle, z, between EC and the plane ABCD

a) \(\hat { DEC } \) = °

b) Angle = °

c) Angle = °

a) \(cos\hat { DEC } \quad =\quad \frac { { \left( \sqrt { 34 } \right) }^{ 2 }+{ \left( \sqrt { 34 } \right) }^{ 2 }-{ 6 }^{ 2 } }{ 2\times \sqrt { 34 } \times \sqrt { 34 } } \\ \hat { DEC } \quad =\quad { cos }^{ -1 }\left( \frac { 34+34-{ 6 }^{ 2 } }{ 2\times 34 } \right) \\ \hat { DEC } \quad =\quad 61.9°\quad (3sf)\)

Could also be done by splitting the triangle in totwo congruent right angled triangles since triangle ECD is isosceles.

b) Extracting a 2D triangle from the 3D situation. Triangle EFG is right angled with sides EF and FG known.

\(y\quad =\quad \hat { FGE } \\ tany\quad =\quad \frac { 4 }{ 3 } \\ y\quad =\quad { tan }^{ -1 }\left( \frac { 4 }{ 3 } \right) \\ y\quad =\quad 53.1°\quad (3sf)\)

c) Extracting a 2D triangle from the 3D situation. Triangle EFC is right angled with sides EF and EC known.

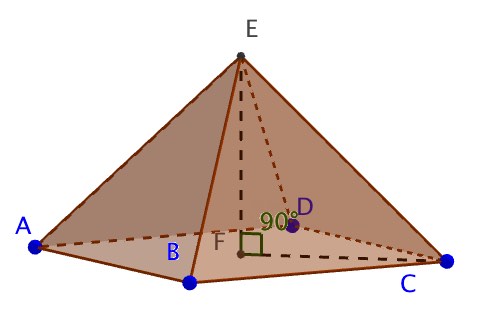\(z\quad =\quad \hat { FCE } \\ sinz\quad =\quad \frac { 4 }{ \sqrt { 34 } } \\ z\quad =\quad { sin }^{ -1 }\left( \frac { 4 }{ \sqrt { 34 } } \right) \\ z\quad =\quad 43.3°\quad (3sf)\)

8

Use the map below to answer the questions

  • The map shows the locations of four boats A, B, C and D
  • The shortest distance from A to B is 1km
  • The shortest distance from B to C is 800m
  • The angle ABC is 100°

a) What is the shortest distance from A to C in km? (to 3sf)

b) Use the result to part a) and the sine rule to work out the angle BCA

  • Angle CBD = 60°
  • The distance BD = 300m

c) What is the distance AD in km? (to 3sf)

  • Angle DAC is 30°
  • Using rounded answers to previous parts of the question

d) What is the distance DC?

a) AC = km

b) Angle BCA = °

c) DIstance AD = km

d) Distance DC = km

a) Looking at the the triangle ABC

\({ AC }^{ 2 }={ 1 }^{ 2 }+{ 0.8 }^{ 2 }-2\times 1\times 0.8\times cos100\\ AC=\sqrt { { 1 }^{ 2 }+{ 0.8 }^{ 2 }-2\times 1\times 0.8\times cos100 } \\ AC\quad =\quad 1.38km\quad (3sf)\)

b) Using AC = 1.38 km

\(\frac { sin\hat { BCA } }{ 1 } =\frac { sin100 }{ 1.38 } \\ sin\hat { BCA } \quad =\quad \frac { sin100 }{ 1.38 } \times 1\\ \hat { BCA } \quad =\quad { sin }^{ -1 }\left( \frac { sin100 }{ 1.38 } \times 1 \right) \\ \hat { BCA } \quad =\quad 45.5°\quad (3sf)\)

c) Looking at Triangle ABD

\({ AD }^{ 2 }={ 1 }^{ 2 }+0.3^{ 2 }-2\times 1\times 0.3\times cos100\\ AD=\sqrt { { 1 }^{ 2 }+{ 0.3 }^{ 2 }-2\times 1\times 0.3\times cos100 } \\ AD\quad =\quad 1.29km\quad (3sf)\)

d) Considering triangle ADC

\({ DC }^{ 2 }={ 1 }.29^{ 2 }+1.38^{ 2 }-2\times 1.29\times 1.38\times cos30\\ DC=\sqrt { { 1 }.29^{ 2 }+1.38^{ 2 }-2\times 1.29\times 1.38\times cos30 } \\ DC\quad =\quad 0.696km\quad (3sf)\)

9

The diagram below shows a metal structure.

  • Give all answers correct to 3sf
  • Use rounded answers in subsequent calculations

a) What is the length AB?

b) What is angle CDB?

c) Which is longer AD or AC?

a) AB = m

b) Angle CDB = °

c) Which is longer AD or DC?

a) \(\frac { AB }{ sin50 } =\frac { 4 }{ sin40 } \\ AB\quad =\quad \frac { 4 }{ sin40 } \times sin50\\ AB\quad =\quad 4.77\quad m\quad (3sf)\)

b) \(\frac { sin\hat { CDB } }{ 4 } =\frac { sin50 }{ 3.5 } \\ sin\hat { CDB } \quad =\quad \frac { sin50 }{ 3.5 } \times 4\\ \hat { CDB } \quad =\quad { sin }^{ -1 }\left( \frac { sin50 }{ 3.5 } \times 4 \right) \\ \hat { CDB } \quad =\quad 61.1°\quad (3sf)\)

c) For the length AD, since angle CDB = 61.1° then ADB must equal 118.9° and so angle DBA must be 21.1°

\(\frac { AD }{ sin21.1 } =\frac { 3.5 }{ sin40 } \\ AD\quad =\quad \frac { 3.5 }{ sin40 } \times sin21.1\\ AD\quad =\quad 1.96\quad m\quad (3sf)\)

For the length AC, since angle CDB is 61.1°, then DBC must be 68.9°

\(\frac { DC }{ sin68.9 } =\frac { 3.5 }{ sin50 } \\ DC\quad =\quad \frac { 3.5 }{ sin50 } \times sin68.9\\ DC\quad =\quad 4.26\quad m\quad (3sf)\)

10

Triangle ABC is the base of a triangular prism as shown in the diagram below

  • The length AB is 10cm
  • The length AC is 13cm
  • The Length BC is 7cm
  • The prism has a depth of 5cm

a) Calculate the angle BAC

b) What is the area of triangle ABC

A line is drawn from the point E down to the mid point of AC, M.

c) How long is that line EM?

d) What angle does the line EM make with the plane ABC

a) Angle BAC = °

b) Area = cm2

c) The line EM has length cm

d) The angle EM makes with the plane ABC = °

a) \(cos\hat { BAC } \quad =\quad \frac { { 10 }^{ 2 }+{ 13 }^{ 2 }-{ 7 }^{ 2 } }{ 2\times 10\times 13 } \\ \hat { BAC } \quad =\quad { cos }^{ -1 }\left( \frac { { 10 }^{ 2 }+{ 13 }^{ 2 }-{ 7 }^{ 2 } }{ 2\times 10\times 13 } \right) \\ \hat { BAC } \quad =\quad 32.2°\quad (3sf)\)

b) \(Area\quad =\quad \frac { 1 }{ 2 } \times 10\times 13\times sin32.2\\ Area\quad =\quad 34.6\quad (3sf)\)

c) and d) Consider the triangle EBM

The angle required is the angle EMB (The angle the line EM makes with the plane ABC)

EB is known as 5cm (depth of prism)

BM can be calculated using the cosine rule as follows.....

\({ BM }^{ 2 }=10^{ 2 }+6.5^{ 2 }-2\times 10\times 6.5\times cos32.2\\ BM=\sqrt { 10^{ 2 }+6.5^{ 2 }-2\times 10\times 6.5\times cos32.2 } \\ BM\quad =\quad 5.68cm\quad (3sf)\)

Now using triangle EBM and BM = 5.68

\(tan\hat { EMB } \quad =\quad \frac { 5 }{ 5.68 } \\ EMB\quad =\quad { tan }^{ -1 }\left( \frac { 5 }{ 5.68 } \right) \\ EMB\quad =\quad 41.4°\quad (3sf)\)

 

Calculus

Concept of Differentiating

1

Another way to find the rate of change of a particular function using a graph is to find the at that point.

 

 

2
Please complete the sentence.

The instantaneous rate of change of a function \(f(x)\) at a point A on a curve is given by the to the curve at point A

3

Find:

\(\lim _{ x\rightarrow 3 }{ (x+4) } \)

This is asking us to find the limit, as x approaches 3, for the expression x+4.

4

Find:

\(\lim _{ x\rightarrow 3 }{ ({ x }^{ 2 }-3) } \)

This is asking us to find the limit, as x approaches 3, for the expression \(x^2-3\).

5

Identify the gradient/rate of change of the following functions

y = 3x +2

y= -5x

y = 7

y = 0.5x - 4

These are all straight line (linear) functions in the form y = mx + c, where m is the gradient. In the case of y = 7, we can think of this as y = 0x + 7 and so the gradient is 0. Graphs like this are horizontal lines so it is logical to conclude that they have gradient = 0.

6

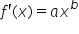Consider the function f left parenthesis x right parenthesis equals 2 x to the power of 5 for which f apostrophe left parenthesis x right parenthesis equals a x to the power of b. What are the values of a and b?

a = , b =

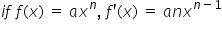
i f space f left parenthesis x right parenthesis space equals space a x to the power of n comma space f apostrophe left parenthesis x right parenthesis space equals space a n x to the power of n minus 1 end exponent

7

Consider the function f left parenthesis x right parenthesis equals 1 over x plus fraction numerator 3 over denominator 4 x squared end fraction, for which f apostrophe left parenthesis x right parenthesis equals a x to the power of b minus c over 2 x to the power of negative d end exponent. What are the values of a, b, c and d? (do it on paper and be careful with the signs)

a = , b= , c = , d =

i f space f left parenthesis x right parenthesis space equals space x to the power of negative 1 end exponent plus 3 over 4 x to the power of negative 2 end exponent space s o space f apostrophe left parenthesis x right parenthesis space equals space minus x to the power of negative 2 end exponent minus 6 over 4 x to the power of negative 3 end exponent space space space space a n d space 6 over 4 equals 3 over 2

8

What is the gradient of the function f left parenthesis x right parenthesis space equals space 4 x squared plus 3 x when x = 2?

Gradient =

f apostrophe left parenthesis x right parenthesis space equals space 8 x plus 3 comma space s u b s t i t u t e space x space equals space 2f apostrophe left parenthesis 2 right parenthesis space equals space 19

9

What is the gradient of the function 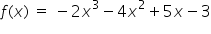f left parenthesis x right parenthesis space equals space minus 2 x cubed minus 4 x squared plus 5 x minus 3 when x = -3?

Gradient =

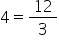
f apostrophe left parenthesis x right parenthesis space equals space minus 6 x squared minus 8 x plus 5 comma space w h e n space x space equals space minus 3f apostrophe left parenthesis negative 3 right parenthesis space equals space minus 54 space minus space minus space 24 space plus space 5 space equals space minus 25

10

Identify the gradient/rate of change of the following functions

y = 7x +2

y= 3x

y = 4

y = 1.5x - 4

These are all straight line (linear) functions in the form y = mx + c, where m is the gradient. In the case of y = 7, we can think of this as y = 0x + 7 and so the gradient is 0. Graphs like this are horizontal lines so it is logical to conclude that they have gradient = 0.

 

Increasing and Decreasing Functions

1

Fill in the missing parts in the following sentences.

If \(f'(x)>0, \)the graph of \(f(x) \) is

Use this optional field for teacher explanations.

2

Fill in the missing parts in the following sentences.

If \(f'(x)=0, \)the graph of \(f(x) \) is

Use this optional field for teacher explanations.

3

Fill in the missing parts in the following sentences.

If \(f'(x)<0, \)the graph of \(f(x) \) is

Use this optional field for teacher explanations.

 

Tangents and Normals

1

Consider the function f(x)=x3+3x2-2x+4, The tangent to this curve at x = -2 is given by y = ax +b. Find the values of a and b

a = , b =

f'(x)=3x2+6x-2, so f'(-2) = -2 Therefore the gradient, a = -2. So you know y = -2x + b, f(-2) = 12 which means the line goes through the point (-2, 12). Now substitute x = -2 and y = 12 (from the gievn point) to get the value of b.

2

Consider the function f(x)=25x2+1x2 , The tangent to this curve at x = 2 is given by y = ax +b. Find the values of a and b.

a = , b =

f(x)=0.4x2+x-2, so f'(x)=0.8x2-2x-3 and f'(2) = 1.35

You can read this from the table function on your GDC. 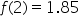f left parenthesis 2 right parenthesis equals 1.85, so the line goes through the point (2, 1.85). Use this to work out the value of c when y = 1.35x + c (since you know that the gradient is 1.35)

3

Find the tangent of \(f(x)=\frac { 8{ x }^{ 2 } }{ 6 } +\frac { { x }^{ 4 } }{ 3 } -5{ x }^{ 2 }+9\) when x = 3.5. If the tangent is \(y=mx+c\), find the values of m and c (with calculator) (Exact or 3.s.f)

\(m=\)

\(c=\)

On GDC; graph; sketch; tangent; x=3.5

4

Find the tangent of \(f(x)=\frac { { x }^{ 3 } }{ 2 } +8{ x }^{ 2 }-x+7\) when x = 2. If the tangent is \(y=mx+c\), find the values of m and c (without a calculator - you may be asked to 'show') (Exact or 3.s.f)

m =

c =

\(f(x)=\frac { { x }^{ 3 } }{ 2 } +8{ x }^{ 2 }-x+7\\ f'(x)=\frac { 3{ x }^{ 2 } }{ 2 } +16x-1\\ at\quad x=2,\quad f(2)=41,\quad f'(2)=37\\ so,\quad at\quad (2,41),\quad m=37\\ Tangent\quad is\quad y=mx+c\\ so\quad y=37x+c,\\ Substitute\quad x=2\quad and\quad y=41\\ 41=37\times 2+c\\ so,\quad c=-33\\ tangent\quad is\quad y=37x-33\)

5

Find the tangent of \(f(x)=\frac { { 3x }^{ 2 } }{ 2 } -6{ x }+9\) when x = 4. If the tangent is \(y=mx+c\), find the values of m and c (without a calculator - you may be asked to 'show') (Exact or 3.s.f)

m =

c =

\(f(x)=\frac { { 3x }^{ 2 } }{ 2 } -6{ x }+9\\ \)

\(f'(x)=3x-6\)

at \( x=4,\quad f(4)=9,\quad f'(4)=6\)

so \((4,9),\quad m=6\\\)

tangent is \( y=mx+c\)

so\(y=6x+c,\)

substitute \( x=4\quad and\quad y=9\)

\(\ 9=6\times 4+c\)

so \(c=-15\)

therefore tangent is \(y=6x-15\)

6

Find the normal of \(f(x)=3{ x }^{ -3 }+\frac { x }{ 4 } -2\) when x = 8. If the normal is \(y=mx+c\), find the values of m and c (with calculator) (3.s.f)

\(m=\)

\(c=\)

On GDC; graph; sketch; normal; x=8

7

Find the normal of \(f(x)=2{ x }^{ 2 }+3x-5\) when x = 3. If the normal is \(y=mx+c\), find the values of m and c (show your working) (3.s.f)

\(m=\)

\(c=\)

\(f(x)=2{ x }^{ 2 }+3x-5\\ f'(x)=4x+3\\ at\quad x=3,\quad f(3)=22,\quad f'(3)=15\\ so,\quad at\quad (3,22),\quad m(tangent)=15\\ Normal\quad is\quad y=-\frac { 1 }{ m } x+c\\ so\quad y=-\frac { 1 }{ 15 } x+c\\ Substitute\quad x=3\quad and\quad y=22\\ 22=-\frac { 1 }{ 15 } \times 3+c\\ so,\quad c=22.2\\ Normal\quad is\quad y=-0.0667x+22.2\)

8

Find the normal of \(f(x)=4{ x }^{ 3 }+2{ x }^{ 2 }+6\) when x = 2. If the normal is \(y=mx+c\), find the values of m and c (show your working)) (3.s.f)

\(m=\)

\(c=\)

\(f(x)=4{ x }^{ 3 }+2{ x }^{ 2 }+6\\ f'(x)=12{ x }^{ 2 }+4x\\ at\quad x=2,\quad f(2)=46,\quad f'(2)=56\\ so,\quad at\quad (2,46),\quad m(tangent)=56\\ Normal\quad is\quad y=-\frac { 1 }{ m } x+c\\ so\quad y=-\frac { 1 }{ 56 } x+c\\ Substitute\quad x=2\quad and\quad y=46\\ 46=-\frac { 1 }{ 56 } \times 2+c\\ so,\quad c=46.0\\ Normal\quad is\quad y=-0.0179x+46.0\)

9

Find the normal of \(f(x)=\frac { 2 }{ { x }^{ 3 } } +3{ x }^{ 2 }-\frac { 4 }{ x } \) when x = 2. If the normal is \(y=mx+c\), find the values of m and c (show your working)) (3.s.f)

\(m=\)

\(c=\)

\(f(x)=\frac { 2 }{ { x }^{ 3 } } +3{ x }^{ 2 }-\frac { 4 }{ x } \\ f'(x)=-6{ x }^{ -4 }+6x+4{ x }^{ -2 }\\ at\quad x=2,\quad f(2)=\frac { 41 }{ 4 } ,\quad f'(2)=\frac { 101 }{ 8 } \\ so,\quad at\quad (2,\frac { 41 }{ 4 } ),\quad m(tangent)=\frac { 101 }{ 8 } \\ Normal\quad is\quad y=-\frac { 1 }{ m } x+c\\ so\quad y=-\frac { 1 }{ (\frac { 101 }{ 8 } ) } x+c\\ Substitute\quad x=2\quad and\quad y=\frac { 41 }{ 4 } \\ \frac { 41 }{ 4 } =-\frac { 1 }{ (\frac { 101 }{ 8 } ) } \times 2+c\\ so,\quad c=10.4\\ Normal\quad is\quad y=-0.0792x+10.4\)

10

Find the normal of \(f(x)=\frac { 1 }{ { x }^{ 2 } } -3{ x }^{ -4 }+{ x }^{ 3 }\) when x = 1. If the normal is \(y=mx+c\), find the values of m and c (show your working)) (3.s.f)

\(m=\)

\(c=\)

\(f(x)=\frac { 1 }{ { x }^{ 2 } } -3{ x }^{ -4 }+{ x }^{ 3 }\\\)

\( f'(x)=-2{ x }^{ -3 }+12{ x }^{ -5 }+3{ x }^{ 2 }\\\)

at \( x=1,\quad f(1)=-1,\quad f'(1)=13\)

\(\\ so,\quad at\quad (1,-1),\quad m(tangent)=13\)

\(\\ Normal\quad is\quad y=-\frac { 1 }{ m } x+c\)

\(\\ so\quad y=-\frac { 1 }{ 13 } x+c\)

Substituting \(x=1\quad and\quad y=-1\)

\(\\ -1=-\frac { 1 }{ 13 } \times 1+c\)

so \(c=-0.923\)

\( Normal\quad is\quad y=-0.0769x-0.923\)

 

Stationary Points

1
The x value at the minimum point on the curve \(y=4x^{2}+kx+38\) is 3. Find the value of k.

First differentiate to find the gradient function:

\(\frac{dy}{dx}=8x+k\)

As the minimum point exists when x=3, set the derivative equal to zero and then solve to find k:

\(0=8\left(3\right)+k\)

\(k=-24\)


2
The x value at the maximum point on the curve \(y=kx^{2}-36x-160\) is -9. Find the value of k.

First differentiate to find the gradient function:

\(\frac{dy}{dx}=2kx-36\)

As the maximum point exists when x=-9, substitute in \(x=-9\) ,set the derivative equal to zero and then solve to find k:

\(0=-18k-36\)

\(k=-2\)


 

Second Derivative

1

In which ways can you classify a stationary point?

These are all correct responses. The most common method in an exam scenario is to use the second derivative. If you find that the second derivative is equal to zero, then do be aware that you also need to check the sign of either the first derivative or second derivative either side of the point to be sure that you have a stationary inflexion point.

2

A model rocket follows a quadratic path, given by the function, \(H(t)=16t-4{ t }^{ 2 }+2\), where H is the height of the rocket in metres and t is the time in seconds. Find the maximum height of the rocket during its path.

Step 1: Differente

\(H'(t)=16-8t\)

Step 2: Find the maximum point when the gradient is equal to zero. It is a maximum because it is a negative quadratic curve.

\(16-8t=0\\ \therefore \quad t=2\)

Step 3: The maximum height occurs 2 seconds after launch. Substitute \(t=2\) into the original function.

\(H(2)=16(2)-4({ 2 }^{ 2 })+2\\H(2)=18\)

 

Optimisation

1

A 30cm long string is shaped to create a rectangle. What width should the shape have to create the biggest possible area?

cm

Length=x

Width=15-x

\(A=\left(15-x\right)x\)

Differentiating:

\(\frac{dA}{dx}=15-2x\)

Where the Area is the maximum, the derivative is equal to zero:

\(0=15-2x\)

At the maximum area, the length is therefore 7.5cm

 

Integration

1

Estimate the area between the curve, \(y=2^x-1\), and the x-axis between \(2 \le x\le5\), using 3 trapezoids.

x2345
y381531

First find the height of each trapezoid, \(h\) using the trapezoid formula, where \(a=2,b=5 \space and \space n=3\)

\(h=\frac{b-a}{n}=\frac{5-2}{3}=1\) (or simply notice that the height of each trapezoid is increasing by 1 in the top row of the table).

Now using the trapezoid rule formula:

\(\int _{ 2 }^{ 5 }{ { 2 }^{ x }-1\quad dx=\frac { 1 }{ 2 } \times 1\times (3+2(8+15)+31)=\space 40\space { units }^{ 2 } } \)

2

Find \(\int { x²\quad dx } \)

Add one to the power and divide by the power