Here we take trigonometry to the next level by working with triangles that do not have a right angle. We will work on three key rules. The Sine rule, the Cosine rule and the formula for th area of a triangle. All of these involve linking four bits of information about a given triangle. When you know three of them you can figure out the fourth. These problems are then extended in to three dimensions.
In this unit you should learn to…
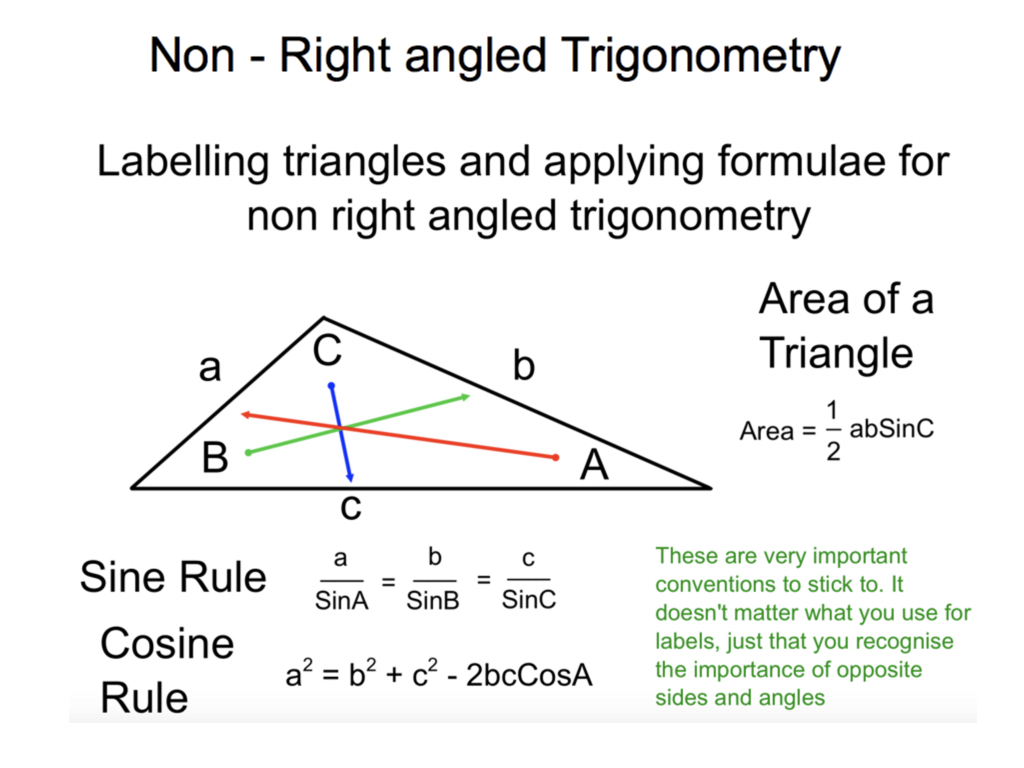
Derive, understand and use the sine rule for solving problems in non right angled trigonometry
Derive, understand and use the cosine rule for solving problems in non right angled trigonometry
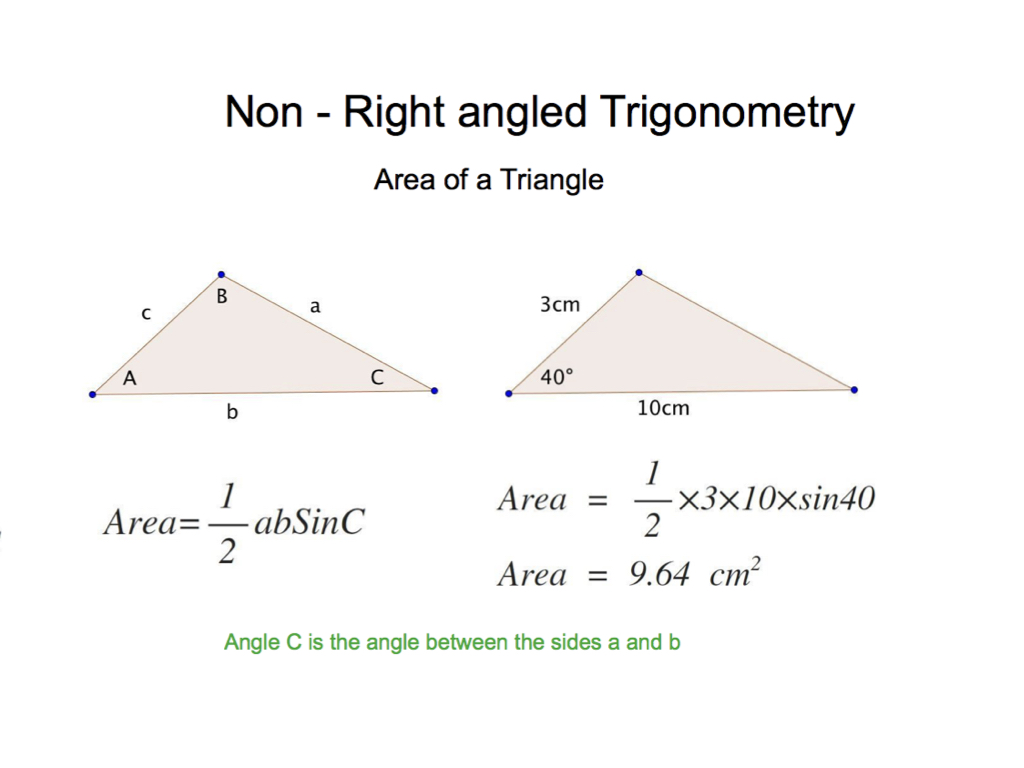
Work out the area of a non right angled triangle using trigonometry
Solve problems involving the above
Successfully using trigonometry with non right angled triangles depends on sticking to these important conventions. The key is recognising pairs of opposite angles and sides.
What is it and how do we use it to solve problems in non right angled triangles.
What is it and how do we use it to solve problems in non right angled triangles.
How to find the area of a triangle with no right angle and thus, without the perpendicular height.
5. Angles between lines and planes
A brief visual to help you understand what is meant by this idea.
This section of the page can be used for quick review. The flashcards help you go over key points and the quiz lets you practice answering questions on this subtopic.
Flash Cards Review this condensed 'key point' flashcard to help you check and keep ideas fresh in your mind.
Self Checking quiz Practice your understanding on these quiz questions. Check your answers when you are done and read the hints where you got stuck. If you find there are still some gaps in your understanding then go back to the videos and slides above.
1
Solve the following equations, giving your answers correct to 3sf
a) \(\frac { a }{ Sin20 } =\frac { 10 }{ sin30 } \) b) \(\frac { 18 }{ sinA } =\frac { 27 }{ sin40 } \) c) \({ a }^{ 2 }={ 7 }^{ 2 }+{ 10 }^{ 2 }-2\times 7\times 10\times cos48\) d) \(cosA\quad =\quad \frac { { 13 }^{ 2 }+{ 20 }^{ 2 }-{ 8 }^{ 2 } }{ 2\times 13\times 20 } \)
a) \(\frac { a }{ sin20 } =\frac { 10 }{ sin30 } \\ a\quad =\quad \frac { 10 }{ sin30 } \times sin20\\ a\quad =\quad 6.84\quad (3sf)\)
b) \(\frac { 18 }{ sinA } =\frac { 27 }{ sin40 } \\ \frac { sinA }{ 18 } =\frac { sin40 }{ 27 } \\ sinA\quad =\quad \frac { sin40 }{ 27 } \times 18\\ A\quad =\quad { sin }^{ -1 }\left( \frac { sin40 }{ 27 } \times 18 \right) \\ A\quad =\quad 25.4°\quad (3sf)\)
c) \({ a }^{ 2 }={ 7 }^{ 2 }+{ 10 }^{ 2 }-2\times 7\times 10\times cos\quad 48\\ a=\sqrt { 149\quad -\quad 140cos48 } \\ a\quad =\quad 7.44\quad (3sf)\)
d) \(cosA\quad =\quad \frac { { 13 }^{ 2 }+{ 20 }^{ 2 }-{ 8 }^{ 2 } }{ 2\times 13\times 20 } \\ A\quad =\quad { cos }^{ -1 }\left( \frac { { 13 }^{ 2 }+{ 20 }^{ 2 }-{ 8 }^{ 2 } }{ 2\times 13\times 20 } \right) \\ A\quad =\quad 13.8° (3sf)\)
2
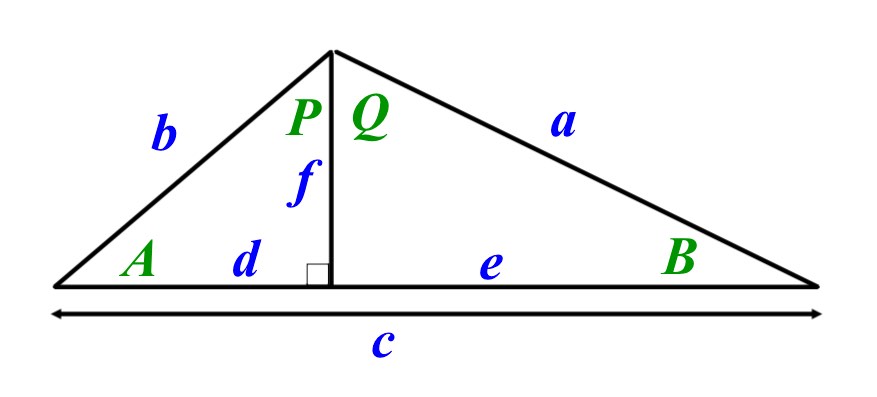
Consider the following diagram
Mark each of the following statements about the diagram as either true (T) or false (F)
a) T - Angles and sides in each fraction are opposite eachother
b) F - Q is not the angle between sides a and c
c) T - B is the angle between a and c
d) T - P + Q is the angle opposite side c and likewise for A and a
3
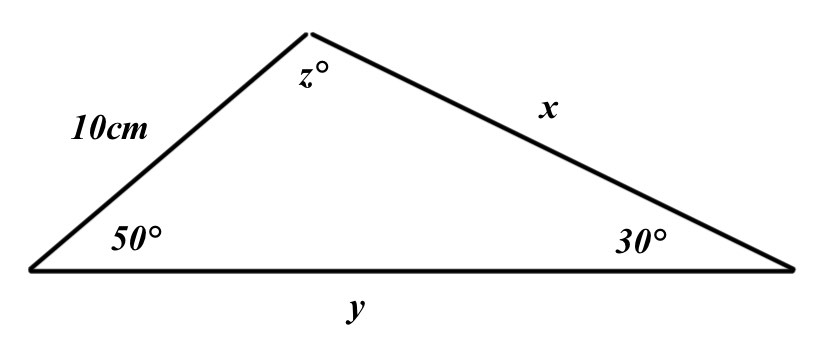
Consider the diagram below.
a) What is the exact value of z?
b) Find the values of x and y (give your answer to 3sf)
a) Since angles in a triangle add up to 180°, z = 100
b) \(\frac { x }{ sin50 } =\frac { 10 }{ sin30 } \\ x\quad =\quad \frac { 10 }{ sin30 } \times sin50\\ x\quad =\quad 15.3\quad cm\quad (3sf)\)
c) \(\frac { y }{ sin100 } =\frac { 10 }{ sin30 } \\ y\quad =\quad \frac { 10 }{ sin30 } \times sin100\\ y\quad =\quad 19.7\quad cm\quad (3sf)\)
4
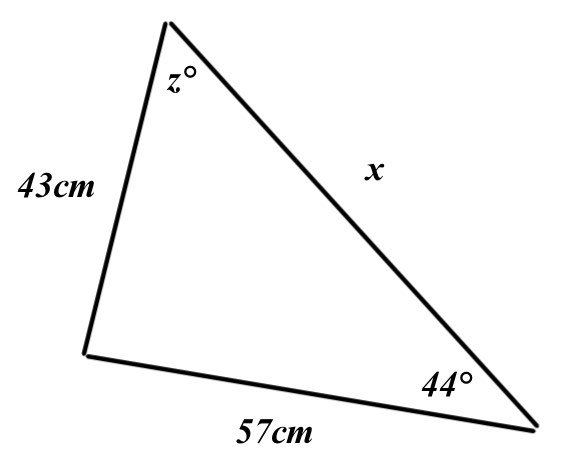
For the triangle below
a) Calculate the value of z to 3sf
b) Use that rounded value for z and the sine rule to work out the value of x
c) Again, use the rounded value of z to calculate the area of the triangle
a) \(\frac { sinz }{ 57 } =\frac { sin44 }{ 43 } \\ sinz\quad =\quad \frac { sin44 }{ 43 } \times 57\\ z\quad =\quad { sin }^{ -1 }\left( \frac { sin44 }{ 43 } \times 57 \right) \\ z\quad =\quad 67.0°\quad (3sf)\)
b) Since z = 67.0° to 3sf, we can calculate that the thrid angle (opposite side x) is 23°
\(\frac { x }{ sin23 } =\frac { 43 }{ sin44 } \\ x\quad =\quad \frac { 43 }{ sin44 } \times sin23\\ y\quad =\quad 24.2\quad cm\quad (3sf)\)
c) \(Area\quad =\quad \frac { 1 }{ 2 } \times 43\times 57\times sin23\\ Area\quad =\quad 479{ cm }^{ 2 }\)
5
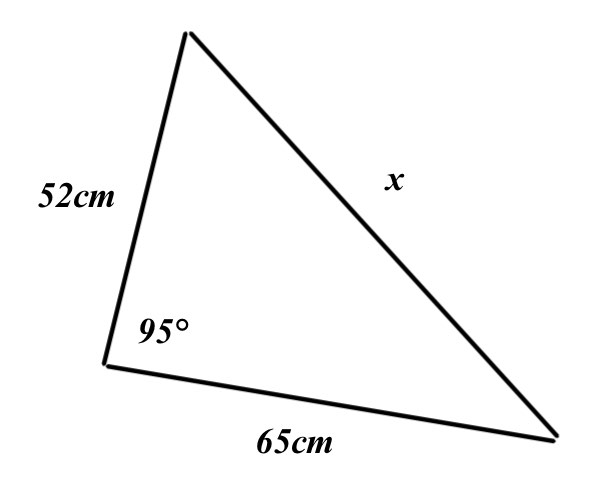
Consider the following diagram
a) Work out the value of x
b) Work out the area of the triangle
a) \({ x }^{ 2 }={ 52 }^{ 2 }+{ 65 }^{ 2 }-2\times 52\times 65\times cos95\\ a=\sqrt { 6929\quad -\quad 3380cos95 } \\ a\quad =\quad 85.0cm\quad (3sf)\)
b) \(Area\quad =\quad \frac { 1 }{ 2 } \times 52\times 65\times sin95\\ Area\quad =\quad 1683.56904\\ Area\quad =\quad 1680\quad { cm }^{ 2 }\quad (3sf)\)
6
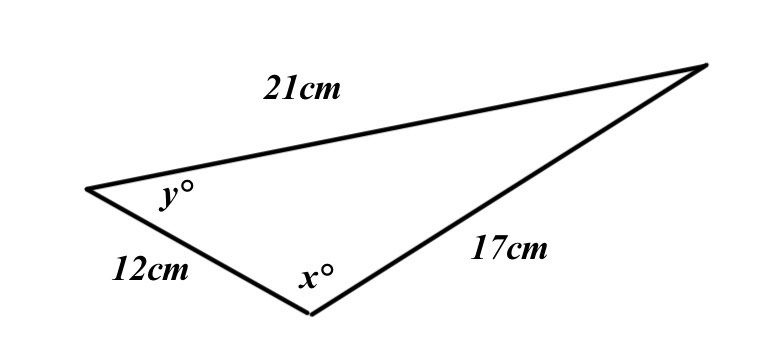
Answer questions referring to the diagram below.
a) Calculate the value of x to 3sf.
b) Calculate the value of y to 3sf.
c) Use the rounded value of x to work out the area of the triangle
a) \(cosx\quad =\quad \frac { { 12 }^{ 2 }+{ 17 }^{ 2 }-{ 21 }^{ 2 } }{ 2\times 12\times 17 } \\ x\quad =\quad { cos }^{ -1 }\left( \frac { { 12 }^{ 2 }+{ 17 }^{ 2 }-{ 21 }^{ 2 } }{ 2\times 12\times 17 } \right) \\ x\quad =\quad 91.1°\)
b) \(cosy\quad =\quad \frac { { 12 }^{ 2 }+{ 21 }^{ 2 }-{ 17 }^{ 2 } }{ 2\times 12\times 21 } \\ y\quad =\quad { cos }^{ -1 }\left( \frac { { 12 }^{ 2 }+{ 21 }^{ 2 }-{ 17 }^{ 2 } }{ 2\times 12\times 21 } \right) \\ y\quad =\quad 54.0°\)
c) \(Area\quad =\quad \frac { 1 }{ 2 } \times 12\times 17\times sin91.1\\ Area\quad =\quad 101.9812026\\ Area\quad =\quad 102\quad { cm }^{ 2 }\quad (3sf)\)
7
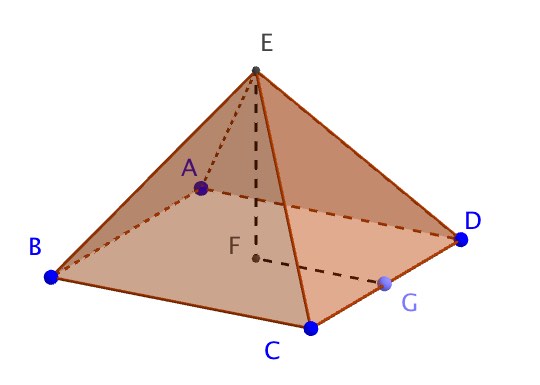
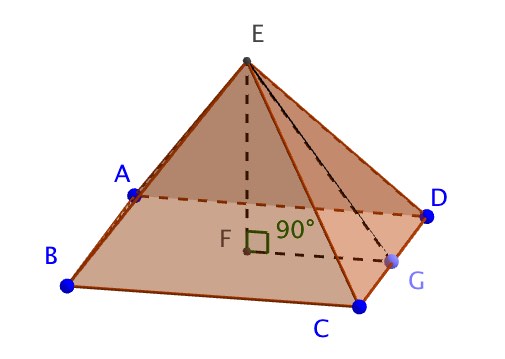
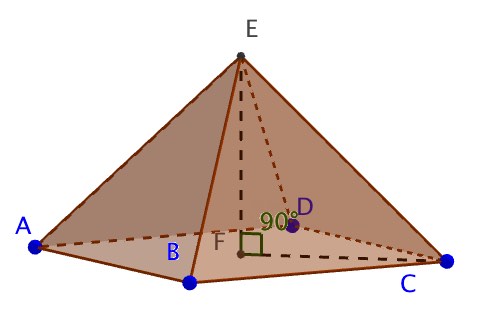
Consider the square based pyramid ABCDE
EF = 4cm, GF = 3cm, CD = 6cm, EC = \(\sqrt { 34 } cm\)
a) What is the angle \(\hat { DEC } \) (to 3sf)
b) What is the angle, y, between FG and the plane ECD
c) What is the angle, z, between EC and the plane ABCD
a) \(cos\hat { DEC } \quad =\quad \frac { { \left( \sqrt { 34 } \right) }^{ 2 }+{ \left( \sqrt { 34 } \right) }^{ 2 }-{ 6 }^{ 2 } }{ 2\times \sqrt { 34 } \times \sqrt { 34 } } \\ \hat { DEC } \quad =\quad { cos }^{ -1 }\left( \frac { 34+34-{ 6 }^{ 2 } }{ 2\times 34 } \right) \\ \hat { DEC } \quad =\quad 61.9°\quad (3sf)\)
Could also be done by splitting the triangle in totwo congruent right angled triangles since triangle ECD is isosceles.
b) Extracting a 2D triangle from the 3D situation. Triangle EFG is right angled with sides EF and FG known.
\(y\quad =\quad \hat { FGE } \\ tany\quad =\quad \frac { 4 }{ 3 } \\ y\quad =\quad { tan }^{ -1 }\left( \frac { 4 }{ 3 } \right) \\ y\quad =\quad 53.1°\quad (3sf)\)
c) Extracting a 2D triangle from the 3D situation. Triangle EFC is right angled with sides EF and EC known.
\(z\quad =\quad \hat { FCE } \\ sinz\quad =\quad \frac { 4 }{ \sqrt { 34 } } \\ z\quad =\quad { sin }^{ -1 }\left( \frac { 4 }{ \sqrt { 34 } } \right) \\ z\quad =\quad 43.3°\quad (3sf)\)
8
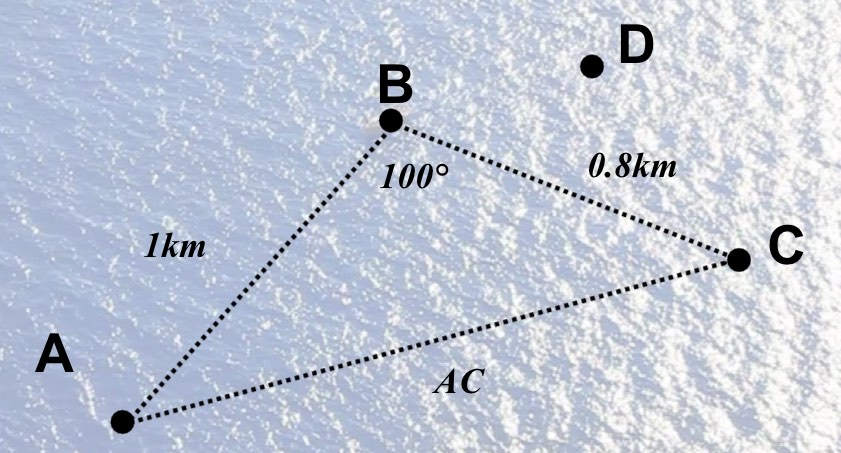
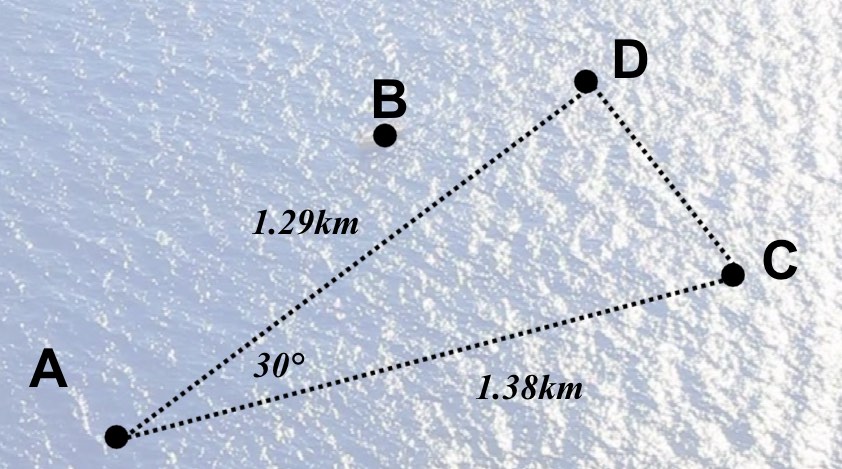
Use the map below to answer the questions
The map shows the locations of four boats A, B, C and D The shortest distance from A to B is 1km The shortest distance from B to C is 800m The angle ABC is 100° a) What is the shortest distance from A to C in km? (to 3sf)
b) Use the result to part a) and the sine rule to work out the angle BCA
Angle CBD = 60° The distance BD = 300m c) What is the distance AD in km? (to 3sf)
Angle DAC is 30° Using rounded answers to previous parts of the question d) What is the distance DC?
a) Looking at the the triangle ABC
\({ AC }^{ 2 }={ 1 }^{ 2 }+{ 0.8 }^{ 2 }-2\times 1\times 0.8\times cos100\\ AC=\sqrt { { 1 }^{ 2 }+{ 0.8 }^{ 2 }-2\times 1\times 0.8\times cos100 } \\ AC\quad =\quad 1.38km\quad (3sf)\)
b) Using AC = 1.38 km
\(\frac { sin\hat { BCA } }{ 1 } =\frac { sin100 }{ 1.38 } \\ sin\hat { BCA } \quad =\quad \frac { sin100 }{ 1.38 } \times 1\\ \hat { BCA } \quad =\quad { sin }^{ -1 }\left( \frac { sin100 }{ 1.38 } \times 1 \right) \\ \hat { BCA } \quad =\quad 45.5°\quad (3sf)\)
c) Looking at Triangle ABD
\({ AD }^{ 2 }={ 1 }^{ 2 }+0.3^{ 2 }-2\times 1\times 0.3\times cos100\\ AD=\sqrt { { 1 }^{ 2 }+{ 0.3 }^{ 2 }-2\times 1\times 0.3\times cos100 } \\ AD\quad =\quad 1.29km\quad (3sf)\)
d) Considering triangle ADC
\({ DC }^{ 2 }={ 1 }.29^{ 2 }+1.38^{ 2 }-2\times 1.29\times 1.38\times cos30\\ DC=\sqrt { { 1 }.29^{ 2 }+1.38^{ 2 }-2\times 1.29\times 1.38\times cos30 } \\ DC\quad =\quad 0.696km\quad (3sf)\)
9
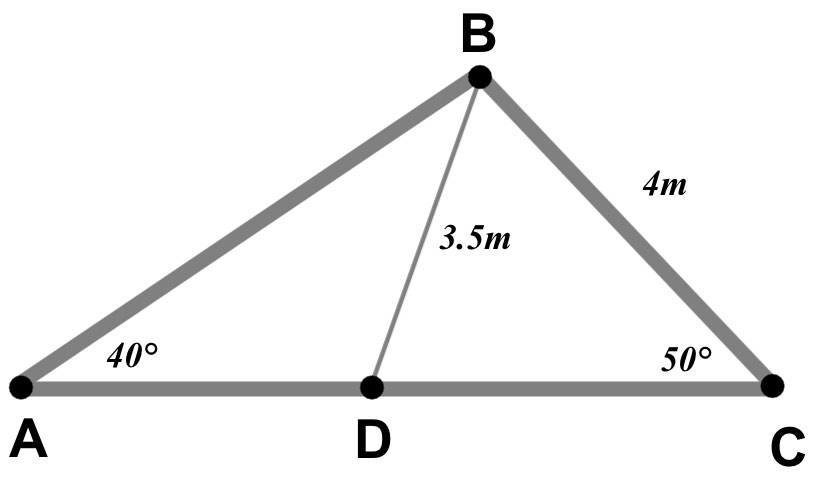
The diagram below shows a metal structure.
Give all answers correct to 3sf Use rounded answers in subsequent calculations a) What is the length AB?
b) What is angle CDB?
c) Which is longer AD or AC?
a) \(\frac { AB }{ sin50 } =\frac { 4 }{ sin40 } \\ AB\quad =\quad \frac { 4 }{ sin40 } \times sin50\\ AB\quad =\quad 4.77\quad m\quad (3sf)\)
b) \(\frac { sin\hat { CDB } }{ 4 } =\frac { sin50 }{ 3.5 } \\ sin\hat { CDB } \quad =\quad \frac { sin50 }{ 3.5 } \times 4\\ \hat { CDB } \quad =\quad { sin }^{ -1 }\left( \frac { sin50 }{ 3.5 } \times 4 \right) \\ \hat { CDB } \quad =\quad 61.1°\quad (3sf)\)
c) For the length AD, since angle CDB = 61.1° then ADB must equal 118.9° and so angle DBA must be 21.1°
\(\frac { AD }{ sin21.1 } =\frac { 3.5 }{ sin40 } \\ AD\quad =\quad \frac { 3.5 }{ sin40 } \times sin21.1\\ AD\quad =\quad 1.96\quad m\quad (3sf)\)
For the length AC, since angle CDB is 61.1°, then DBC must be 68.9°
\(\frac { DC }{ sin68.9 } =\frac { 3.5 }{ sin50 } \\ DC\quad =\quad \frac { 3.5 }{ sin50 } \times sin68.9\\ DC\quad =\quad 4.26\quad m\quad (3sf)\)
10
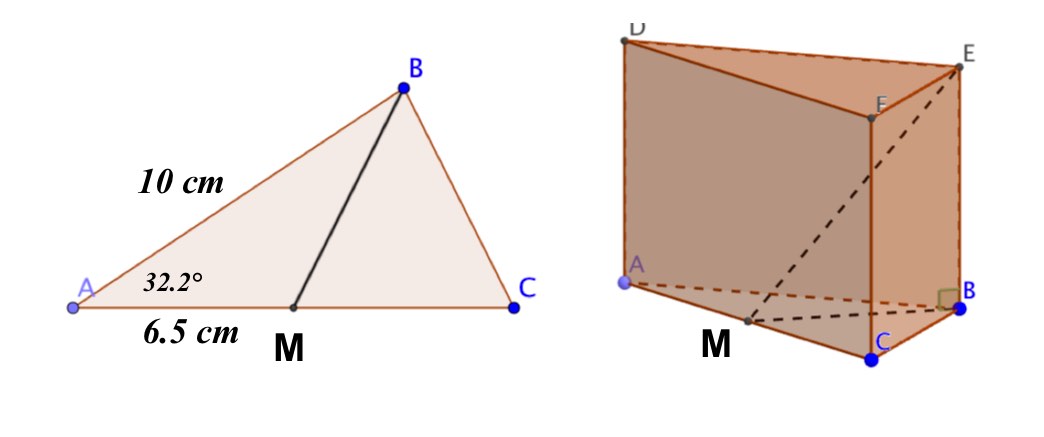
Triangle ABC is the base of a triangular prism as shown in the diagram below
The length AB is 10cm The length AC is 13cm The Length BC is 7cm The prism has a depth of 5cm a) Calculate the angle BAC
b) What is the area of triangle ABC
A line is drawn from the point E down to the mid point of AC, M.
c) How long is that line EM?
d) What angle does the line EM make with the plane ABC
a) \(cos\hat { BAC } \quad =\quad \frac { { 10 }^{ 2 }+{ 13 }^{ 2 }-{ 7 }^{ 2 } }{ 2\times 10\times 13 } \\ \hat { BAC } \quad =\quad { cos }^{ -1 }\left( \frac { { 10 }^{ 2 }+{ 13 }^{ 2 }-{ 7 }^{ 2 } }{ 2\times 10\times 13 } \right) \\ \hat { BAC } \quad =\quad 32.2°\quad (3sf)\)
b) \(Area\quad =\quad \frac { 1 }{ 2 } \times 10\times 13\times sin32.2\\ Area\quad =\quad 34.6\quad (3sf)\)
c) and d) Consider the triangle EBM
The angle required is the angle EMB (The angle the line EM makes with the plane ABC)
EB is known as 5cm (depth of prism)
BM can be calculated using the cosine rule as follows.....
\({ BM }^{ 2 }=10^{ 2 }+6.5^{ 2 }-2\times 10\times 6.5\times cos32.2\\ BM=\sqrt { 10^{ 2 }+6.5^{ 2 }-2\times 10\times 6.5\times cos32.2 } \\ BM\quad =\quad 5.68cm\quad (3sf)\)
Now using triangle EBM and BM = 5.68
\(tan\hat { EMB } \quad =\quad \frac { 5 }{ 5.68 } \\ EMB\quad =\quad { tan }^{ -1 }\left( \frac { 5 }{ 5.68 } \right) \\ EMB\quad =\quad 41.4°\quad (3sf)\)
The following questions are based on IB exam style questions from past exams. You should print these off (from the document at the top) and try to do these questions under exam conditions. Then you can check your work with the video solution.
Video solution
Video solution
Video solution
MY PROGRESS
Self-assessment How much of 3.2 Non-right angled trigonometry have you understood?
My notes
Which of the following best describes your feedback?
 Trigonometry for all triangles
Trigonometry for all triangles




















 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn