Exponents
The exponents of a number tell us how many times the number has been multiplied. Understanding these well, and being able to apply the laws of exponents will help us when sketching graphs, using calculus, and working with very large or very small numbers.
In this unit you should learn to…
- Use the basic laws of exponents
- Understand the concepts of logarithms
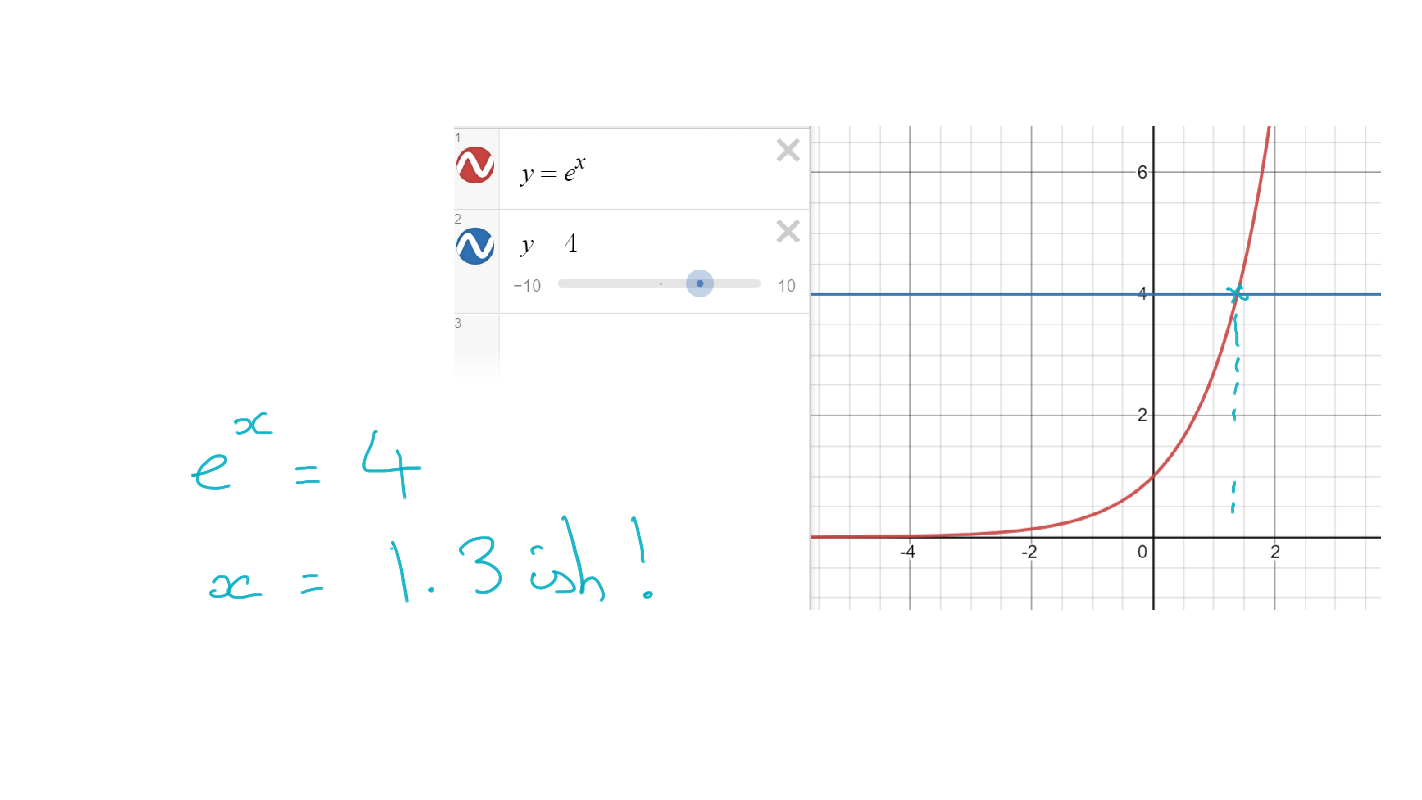
- Evaluate logarithms and exponents using technology
Quiz
Practice your understanding on these quiz questions. Check your answers when you are done and read the worked solutions when you get stuck. If you find there are still some gaps in your understanding then go back to the videos above.
Find
\({ 5 }^{ -2 }\times { 5 }^{ 5 }\)
When the bases are the same, multiply the exponents only.
\({ =5 }^{ (-2+5) }\)
Simplify
\({ { (2 }^{ 3 }) }^{ 4 }\)
This is equivalent to \({ { 2 }^{ 3 } } \times { { 2 }^{ 3 } } \times{ { 2 }^{ 3 } } \times { { 2 }^{ 3 } } .\) As the bases are the same we can now simply add together the exponents.
Simplify
\(3{ y }^{ -2 } \)
\(3{ y }^{ -2 }=3{ \quad \times \quad y }^{ -2 }\)
\({ y }^{ -2 }=\frac { 1 }{ y^2 } \)
Therefore
\({ 3y }^{ -2 }=3\times \frac { 1 }{ y^2 } \)
If \({ a }^{ 3 }\times { a }^{ 4 }={ a }^{ n }\), what is \(n\)?
n =
\({ a }^{ m }\times { a }^{ n }={ a }^{ m+n }\)
If \({ ({ 2p }^{ 3 }) }^{ 2 }=a{ p }^{ n }\), what are the values of \(a\) and \(n\)?
a =
n =
\({ ({ 2p }^{ 3 }) }^{ 2 }={ 2 }^{ 2 }\times { p }^{ 3\times 2 }=4{ p }^{ 6 }\)
If \({ 5 }^{ -1 } =n\), what is the value of \(n\)? (Without a calculator)
n =
If \({ ({ 3 }^{ 0 }) }^{ -3 }=\frac { m }{ n } \), what are the values of \(m\) and \(n\)? (Without a calculator)
m =
n =
If \({ (\frac { { 9x }^{ 5 } }{ { 4y }^{ 7 } } ) }^{ -3 }=\frac { a{ y }^{ b } }{ m{ x }^{ n } } \), what are the values of \(a\), \(b\), \(m\) and \(n\)?
a =
b =
m =
n =
If \({ (\frac { { 4a }^{ 3 }\times 2{ a } }{ { 12{ a }^{ 4 }\times a } } ) }^{ -3 }=\frac { { ma }^{ n } }{ x{ a }^{ y } } \), what are the values of \(m\), \(n\), \(x\) and \(y\)?
m =
n =
x =
y =
If \(\frac { 5 }{ { a }^{ 4 } } \times { 3a }^{ 8 }=m{ a }^{ n }\), what are the values of \(m\) and \(n\)?
m =
n =
The following questions are based on IB exam style questions from past exams. You should print these off (from the document at the top) and try to do these questions under exam conditions. Then you can check your work with the video solution.
How much of 1.5 Exponents and Logarithms have you understood?





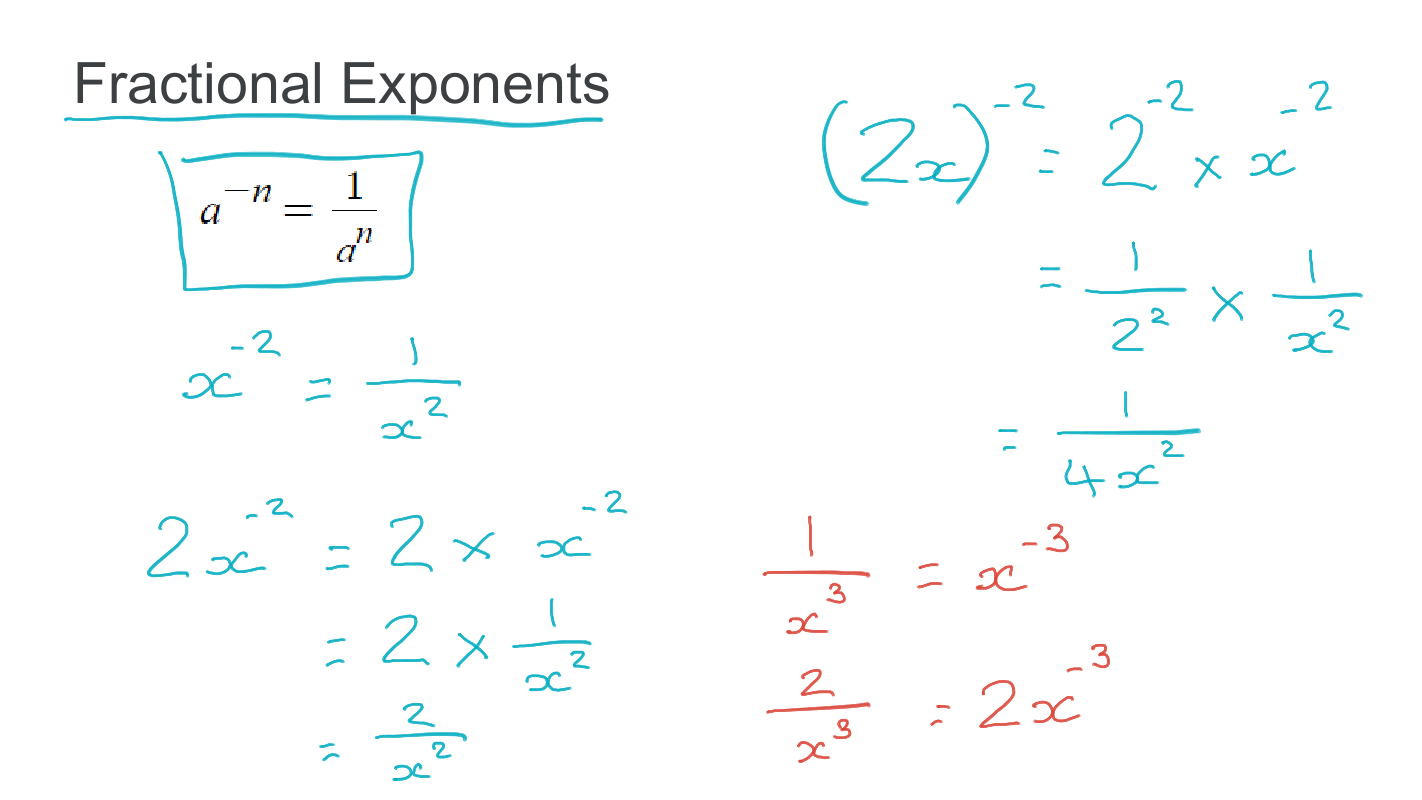










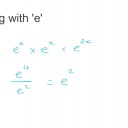


 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn