 What are the chances?
What are the chances?
In this unit you should learn to…
-
recognise key terms
-
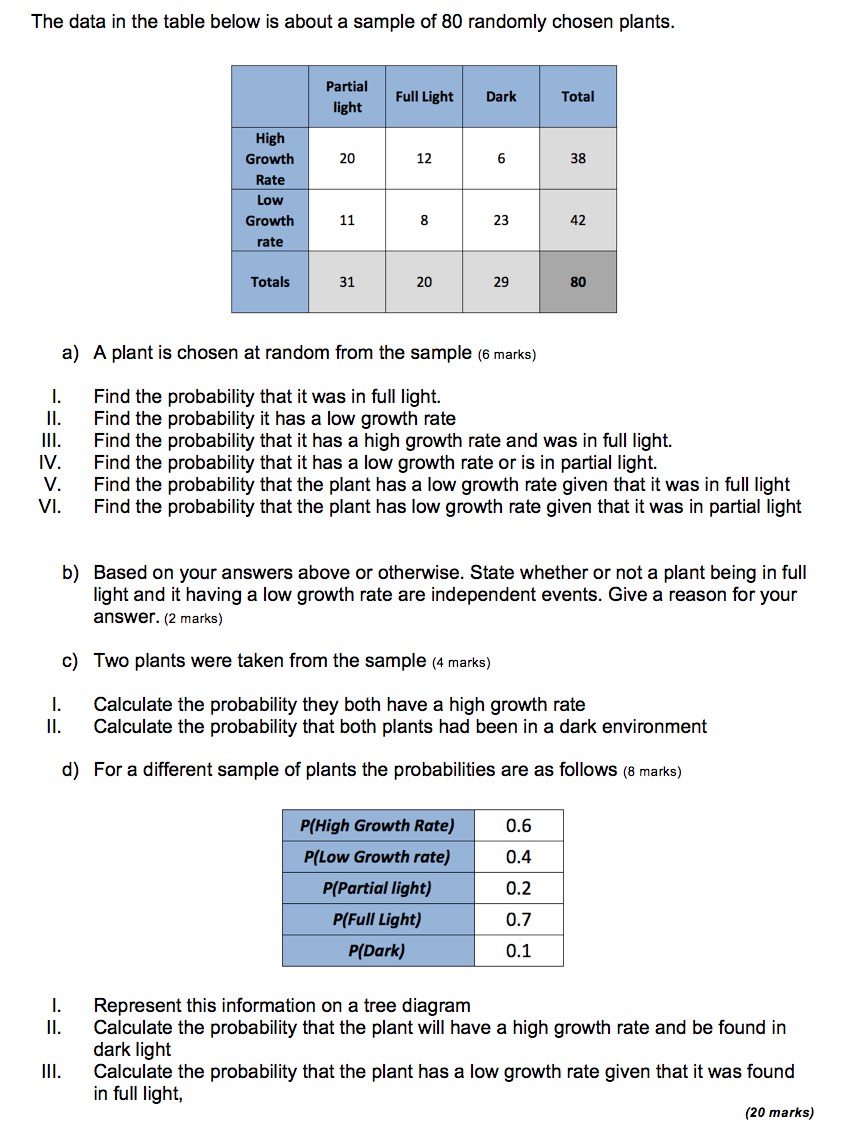
calculate using sample space diagrams
-
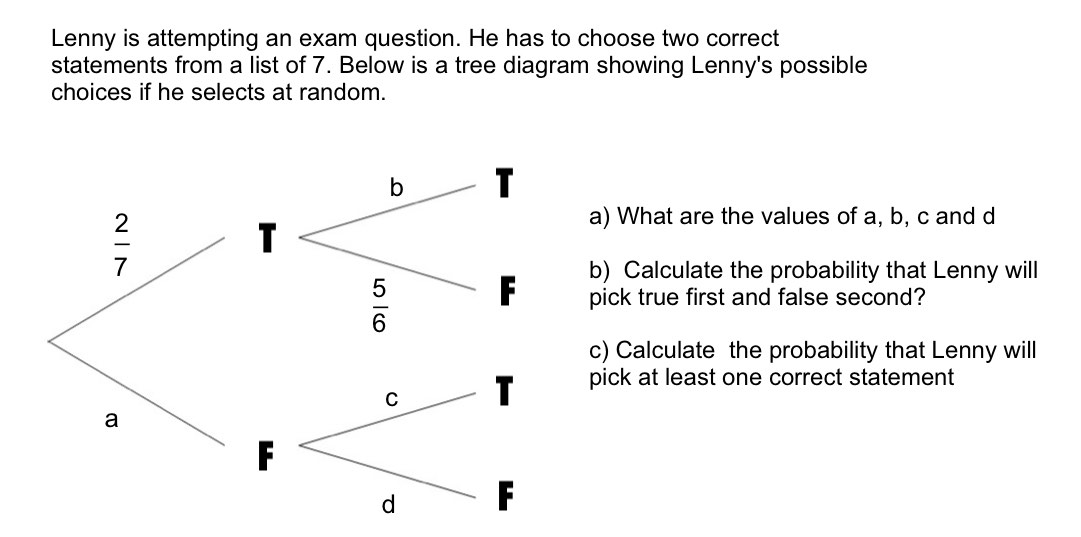
use tree diagrams
-
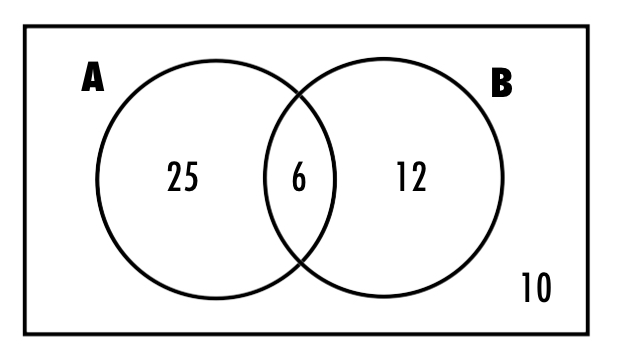
find probabilities from tables and Venn diagrams
-
use conditional probability
This is an introduction to the key ideas and terms in this study of probability.
This section of the page can be used for quick review. The flashcards help you go over key points and the quiz lets you practice answering questions on this subtopic.
Revision Cards
Review these condensed 'key point' revision cards to help you check and keep ideas fresh in your mind.
Self Checking Quiz
Practice your understanding on these quiz questions. Check your answers when you are done and read the hints where you got stuck. If you find there are still some gaps in your understanding then go back to the videos and slides above.
How much of 4.5 & 4.6 Probability have you understood?





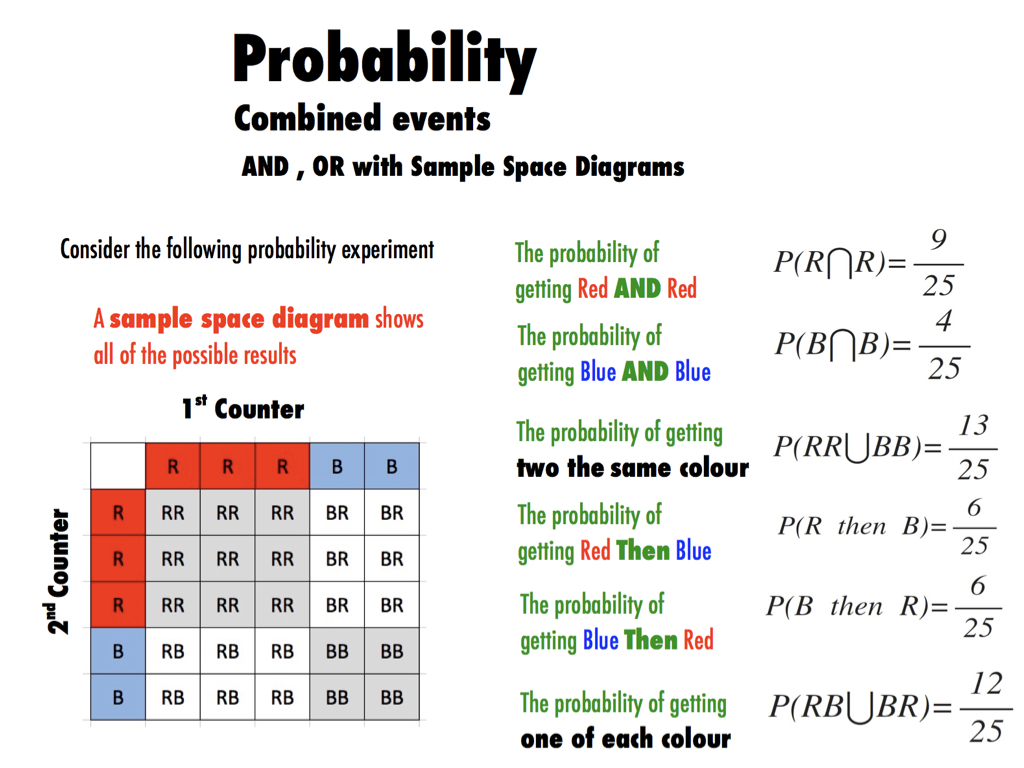

















































 Consider an 8 sided dice. The dice is unbiased and the sides are numbered from 1 to 8. Fill the gaps to give the respective probabilities. (Your answers are expected as exact decimals between 0 and 1, for example 0.65)
Consider an 8 sided dice. The dice is unbiased and the sides are numbered from 1 to 8. Fill the gaps to give the respective probabilities. (Your answers are expected as exact decimals between 0 and 1, for example 0.65) A 10 side dice is rolled (unbiased, numbered from 1 to 10) and a a four coloured spinner is spun (unbiased and equally divided between Red, Green, Blue and Orange)
A 10 side dice is rolled (unbiased, numbered from 1 to 10) and a a four coloured spinner is spun (unbiased and equally divided between Red, Green, Blue and Orange)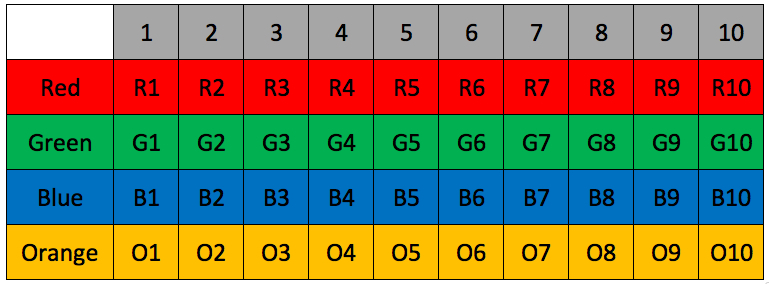

 In a party bag of chocolates there are 3 purple and 7 red chocolates. You select 1 of them at random (Without looking) and eat it! Then you go back for a second one, also without looking. The following tree diagram shows the possible outcomes on a tree diagram.
In a party bag of chocolates there are 3 purple and 7 red chocolates. You select 1 of them at random (Without looking) and eat it! Then you go back for a second one, also without looking. The following tree diagram shows the possible outcomes on a tree diagram.




 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn