
In this unit you should learn to…
-
understand what types of data are binomially distributed
-
be familiar using binomial notation
-
calculate the expected value, standard deviation and variance of a binomially distributed event
-
calculate probability using the binomial distribution
-
calculate probability using the binomial distribution
The following questions are based on IB exam style questions from past exams. You should print these off (from the document at the top) and try to do these questions under exam conditions. Then you can check your work with the video solution.
Ms Roberts teaches a Maths class with 17 students. 6 of them are working from school, and 11 of them are working remotely.
Each day, Ms Roberts chooses one student at random to make a presentation.
a. Find the probability that on a given day, Ms Roberts chooses someone who is working from home (1)
In September, Ms Roberts will teach 15 lessons with her class.
b. Find the probability that she chooses a student working remotely 8 times. (2)
c. Find the probability that she chooses a student working in school at least 9 times. (3)
(6 marks)
Video Solution
How much of 4.8 Binomial Distribution have you understood?







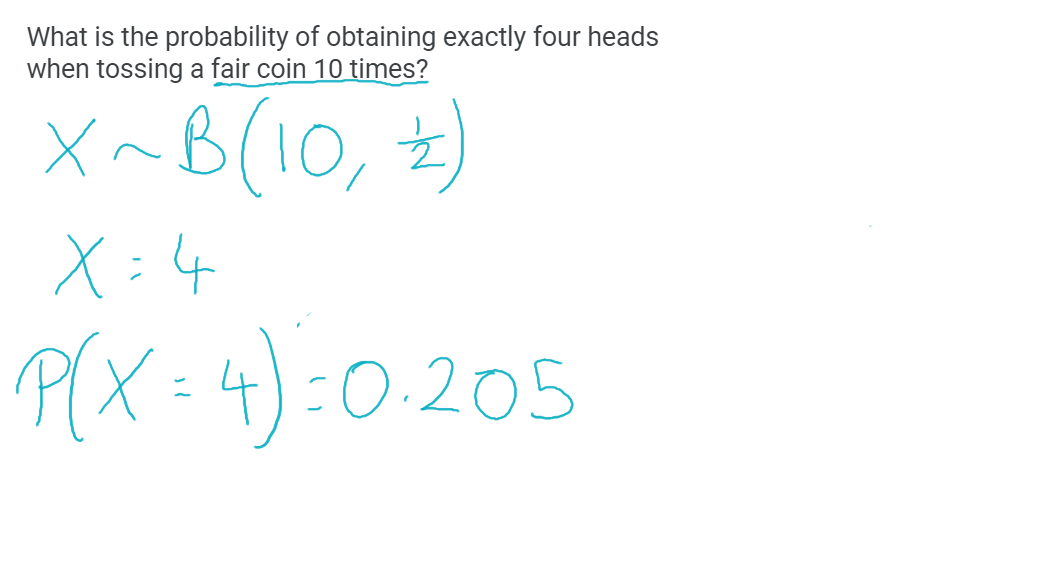









 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn