
In this section of the course you will learn about an area of calculus called integration. This an be considered in multiple ways, both as the inverse of differentiation (anti-differentiation) and in finding areas under curves. We will also use the trapezoidal rule to estimate the area under a curve.
In this unit you should learn to...
- Integrate polynomial functions.
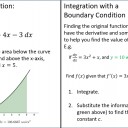
- Find an original function through integration (anti-differentiation) with a boundary condition.
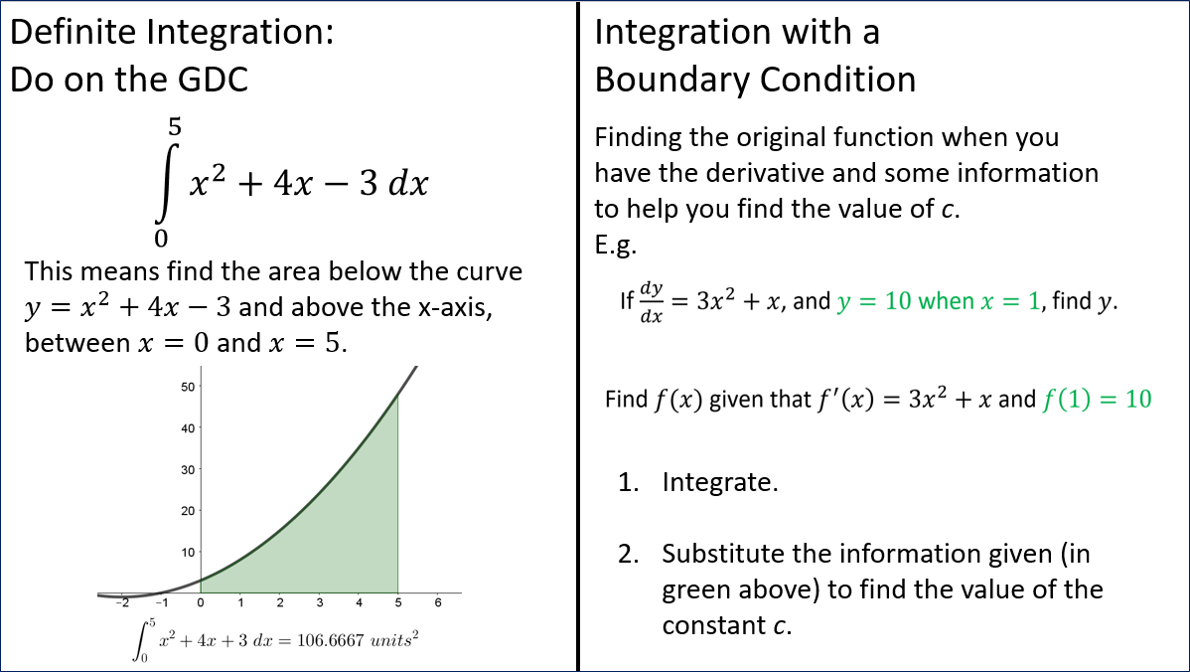
- Evaluate definite integrals on the GDC and hence find the area between a curve, the x-axis and an upper and lower bound.
- Estimate areas under curves using the trapezoidal rule.
Keep track of your progress on this page and practice the exam questions on this Integration and Trapezoidal Rule activity sheet.
Have you ever wondered about the connection between the area and circumference of a circle?
If you integrate the circumference you obtain the area:
\(\int_{0}^{r}2\pi r\ dr\ =\ \pi r^{2}\)
Why?
The integral sign actually stands for "infinite sum". That's the reason why it looks like an elongated "S" shape. So the the equation above means the following:
If you draw an infinite number of smaller circles inside a circle, then sum all of the infinite circumferences, then those infinite lines added up give you an area (the more lengths you add, the closer you'll get to the area).
.png)
How much of 5.5 & 5.8 Integration and Trapezoidal rule have you understood?






.png)
.png)
.png)
.png)
 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn