| Date | May 2017 | Marks available | 3 | Reference code | 17M.2.hl.TZ1.12 |
| Level | HL only | Paper | 2 | Time zone | TZ1 |
| Command term | Sketch | Question number | 12 | Adapted from | N/A |
Question
Consider \(f(x) = - 1 + \ln \left( {\sqrt {{x^2} - 1} } \right)\)
The function \(f\) is defined by \(f(x) = - 1 + \ln \left( {\sqrt {{x^2} - 1} } \right),{\text{ }}x \in D\)
The function \(g\) is defined by \(g(x) = - 1 + \ln \left( {\sqrt {{x^2} - 1} } \right),{\text{ }}x \in \left] {1,{\text{ }}\infty } \right[\).
Find the largest possible domain \(D\) for \(f\) to be a function.
Sketch the graph of \(y = f(x)\) showing clearly the equations of asymptotes and the coordinates of any intercepts with the axes.
Explain why \(f\) is an even function.
Explain why the inverse function \({f^{ - 1}}\) does not exist.
Find the inverse function \({g^{ - 1}}\) and state its domain.
Find \(g'(x)\).
Hence, show that there are no solutions to \(g'(x) = 0\);
Hence, show that there are no solutions to \(({g^{ - 1}})'(x) = 0\).
Markscheme
\({x^2} - 1 > 0\) (M1)
\(x < - 1\) or \(x > 1\) A1
[2 marks]
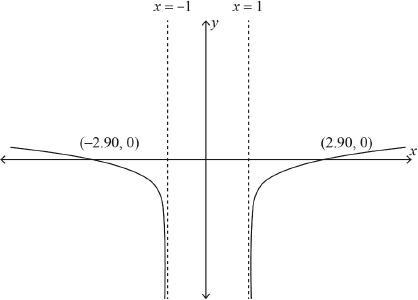
shape A1
\(x = 1\) and \(x = - 1\) A1
\(x\)-intercepts A1
[3 marks]
EITHER
\(f\) is symmetrical about the \(y\)-axis R1
OR
\(f( - x) = f(x)\) R1
[1 mark]
EITHER
\(f\) is not one-to-one function R1
OR
horizontal line cuts twice R1
Note: Accept any equivalent correct statement.
[1 mark]
\(x = - 1 + \ln \left( {\sqrt {{y^2} - 1} } \right)\) M1
\({{\text{e}}^{2x + 2}} = {y^2} - 1\) M1
\({g^{ - 1}}(x) = \sqrt {{{\text{e}}^{2x + 2}} + 1} ,{\text{ }}x \in \mathbb{R}\) A1A1
[4 marks]
\(g'(x) = \frac{1}{{\sqrt {{x^2} - 1} }} \times \frac{{2x}}{{2\sqrt {{x^2} - 1} }}\) M1A1
\(g'(x) = \frac{x}{{{x^2} - 1}}\) A1
[3 marks]
\(g'(x) = \frac{x}{{{x^2} - 1}} = 0 \Rightarrow x = 0\) M1
which is not in the domain of \(g\) (hence no solutions to \(g'(x) = 0\)) R1
[2 marks]
\(({g^{ - 1}})'(x) = \frac{{{{\text{e}}^{2x + 2}}}}{{\sqrt {{{\text{e}}^{2x + 2}} + 1} }}\) M1
as \({{\text{e}}^{2x + 2}} > 0 \Rightarrow ({g^{ - 1}})'(x) > 0\) so no solutions to \(({g^{ - 1}})'(x) = 0\) R1
Note: Accept: equation \({{\text{e}}^{2x + 2}} = 0\) has no solutions.
[2 marks]

