| Date | May 2014 | Marks available | 2 | Reference code | 14M.2.hl.TZ2.14 |
| Level | HL only | Paper | 2 | Time zone | TZ2 |
| Command term | Sketch | Question number | 14 | Adapted from | N/A |
Question
Particle A moves such that its velocity \(v{\text{ m}}{{\text{s}}^{ - 1}}\), at time t seconds, is given by \(v(t) = \frac{t}{{12 + {t^4}}},{\text{ }}t \geqslant 0\).
Particle B moves such that its velocity \(v{\text{ m}}{{\text{s}}^{ - 1}}\) is related to its displacement \(s{\text{ m}}\), by the equation \(v(s) = \arcsin \left( {\sqrt s } \right)\).
Sketch the graph of \(y = v(t)\). Indicate clearly the local maximum and write down its coordinates.
Use the substitution \(u = {t^2}\) to find \(\int {\frac{t}{{12 + {t^4}}}{\text{d}}t} \).
Find the exact distance travelled by particle \(A\) between \(t = 0\) and \(t = 6\) seconds.
Give your answer in the form \(k\arctan (b),{\text{ }}k,{\text{ }}b \in \mathbb{R}\).
Find the acceleration of particle B when \(s = 0.1{\text{ m}}\).
Markscheme
(a)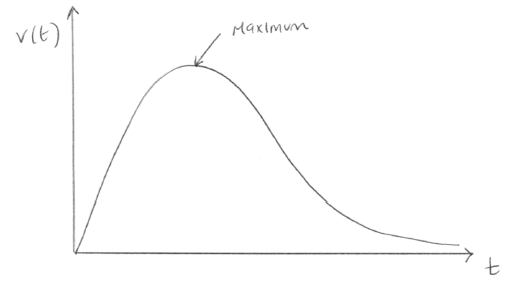 A1
A1
A1 for correct shape and correct domain
\((1.41,{\text{ }}0.0884){\text{ }}\left( {\sqrt 2 ,{\text{ }}\frac{{\sqrt 2 }}{{16}}} \right)\) A1
[2 marks]
EITHER
\(u = {t^2}\)
\(\frac{{{\text{d}}u}}{{{\text{d}}t}} = 2t\) A1
OR
\(t = {u^{\frac{1}{2}}}\)
\(\frac{{{\text{d}}t}}{{{\text{d}}u}} = \frac{1}{2}{u^{ - \frac{1}{2}}}\) A1
THEN
\(\int {\frac{t}{{12 + {t^4}}}{\text{d}}t = \frac{1}{2}\int {\frac{{{\text{d}}u}}{{12 + {u^2}}}} } \) M1
\( = \frac{1}{{2\sqrt {12} }}\arctan \left( {\frac{u}{{\sqrt {12} }}} \right)( + c)\) M1
\( = \frac{1}{{4\sqrt 3 }}\arctan \left( {\frac{{{t^2}}}{{2\sqrt 3 }}} \right)( + c)\) or equivalent A1
[4 marks]
\(\int_0^6 {\frac{t}{{12 + {t^4}}}{\text{d}}t} \) (M1)
\( = \left[ {\frac{1}{{4\sqrt 3 }}\arctan \left( {\frac{{{t^2}}}{{2\sqrt 3 }}} \right)} \right]_0^6\) M1
\( = \frac{1}{{4\sqrt 3 }}\left( {\arctan \left( {\frac{{36}}{{2\sqrt 3 }}} \right)} \right){\text{ }}\left( { = \frac{1}{{4\sqrt 3 }}\left( {\arctan \left( {\frac{{18}}{{\sqrt 3 }}} \right)} \right)} \right){\text{ (m)}}\) A1
Note: Accept \(\frac{{\sqrt 3 }}{{12}}\arctan \left( {6\sqrt 3 } \right)\) or equivalent.
[3 marks]
\(\frac{{{\text{d}}v}}{{{\text{d}}s}} = \frac{1}{{2\sqrt {s(1 - s)} }}\) (A1)
\(a = v\frac{{{\text{d}}v}}{{{\text{d}}s}}\)
\(a = \arcsin \left( {\sqrt s } \right) \times \frac{1}{{2\sqrt {s(1 - s)} }}\) (M1)
\(a = \arcsin \left( {\sqrt {0.1} } \right) \times \frac{1}{{2\sqrt {0.1 \times 0.9} }}\)
\(a = 0.536{\text{ (m}}{{\text{s}}^{ - 2}})\) A1
[3 marks]

