| Date | May 2017 | Marks available | 1 | Reference code | 17M.1.hl.TZ1.11 |
| Level | HL only | Paper | 1 | Time zone | TZ1 |
| Command term | Factorize | Question number | 11 | Adapted from | N/A |
Question
Consider the function \(f(x) = \frac{1}{{{x^2} + 3x + 2}},{\text{ }}x \in \mathbb{R},{\text{ }}x \ne - 2,{\text{ }}x \ne - 1\).
Express \({x^2} + 3x + 2\) in the form \({(x + h)^2} + k\).
Factorize \({x^2} + 3x + 2\).
Sketch the graph of \(f(x)\), indicating on it the equations of the asymptotes, the coordinates of the \(y\)-intercept and the local maximum.
Show that \(\frac{1}{{x + 1}} - \frac{1}{{x + 2}} = \frac{1}{{{x^2} + 3x + 2}}\).
Hence find the value of \(p\) if \(\int_0^1 {f(x){\text{d}}x = \ln (p)} \).
Sketch the graph of \(y = f\left( {\left| x \right|} \right)\).
Determine the area of the region enclosed between the graph of \(y = f\left( {\left| x \right|} \right)\), the \(x\)-axis and the lines with equations \(x = - 1\) and \(x = 1\).
Markscheme
\({x^2} + 3x + 2 = {\left( {x + \frac{3}{2}} \right)^2} - \frac{1}{4}\) A1
[1 mark]
\({x^2} + 3x + 2 = (x + 2)(x + 1)\) A1
[1 mark]
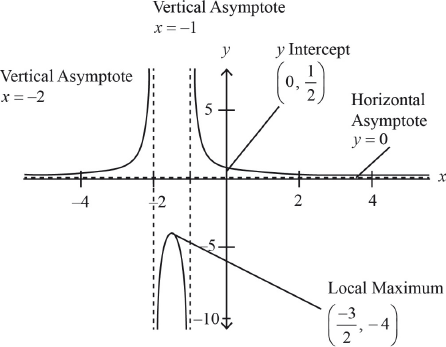
A1 for the shape
A1 for the equation \(y = 0\)
A1 for asymptotes \(x = - 2\) and \(x = - 1\)
A1 for coordinates \(\left( { - \frac{3}{2},{\text{ }} - 4} \right)\)
A1 \(y\)-intercept \(\left( {0,{\text{ }}\frac{1}{2}} \right)\)
[5 marks]
\(\frac{1}{{x + 1}} - \frac{1}{{x + 2}} = \frac{{(x + 2) - (x + 1)}}{{(x + 1)(x + 2)}}\) M1
\( = \frac{1}{{{x^2} + 3x + 2}}\) AG
[1 mark]
\(\int\limits_0^1 {\frac{1}{{x + 1}} - \frac{1}{{x + 2}}{\text{d}}x} \)
\( = \left[ {\ln (x + 1) - \ln (x + 2)} \right]_0^1\) A1
\( = \ln 2 - \ln 3 - \ln 1 + \ln 2\) M1
\( = \ln \left( {\frac{4}{3}} \right)\) M1A1
\(\therefore p = \frac{4}{3}\)
[4 marks]
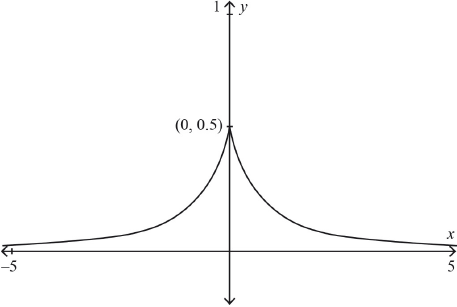
symmetry about the \(y\)-axis M1
correct shape A1
Note: Allow FT from part (b).
[2 marks]
\(2\int_0^1 {f(x){\text{d}}x} \) (M1)(A1)
\( = 2\ln \left( {\frac{4}{3}} \right)\) A1
Note: Do not award FT from part (e).
[3 marks]

