| Date | May 2015 | Marks available | 5 | Reference code | 15M.1.hl.TZ1.11 |
| Level | HL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find and Justify | Question number | 11 | Adapted from | N/A |
Question
Let \(y(x) = x{e^{3x}},{\text{ }}x \in \mathbb{R}\).
Find \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\).
Prove by induction that \(\frac{{{{\text{d}}^n}y}}{{{\text{d}}{x^n}}} = n{3^{n - 1}}{{\text{e}}^{3x}} + x{3^n}{{\text{e}}^{3x}}\) for \(n \in {\mathbb{Z}^ + }\).
Find the coordinates of any local maximum and minimum points on the graph of \(y(x)\).
Justify whether any such point is a maximum or a minimum.
Find the coordinates of any points of inflexion on the graph of \(y(x)\). Justify whether any such point is a point of inflexion.
Hence sketch the graph of \(y(x)\), indicating clearly the points found in parts (c) and (d) and any intercepts with the axes.
Markscheme
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 1 \times {{\text{e}}^{3x}} + x \times 3{{\text{e}}^{3x}} = ({{\text{e}}^{3x}} + 3x{{\text{e}}^{3x}})\) M1A1
[2 marks]
let \(P(n)\) be the statement \(\frac{{{{\text{d}}^n}y}}{{{\text{d}}{x^n}}} = n{3^{n - 1}}{{\text{e}}^{3x}} + x{3^n}{{\text{e}}^{3x}}\)
prove for \(n = 1\) M1
\(LHS\) of \(P(1)\) is \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) which is \(1 \times {{\text{e}}^{3x}} + x \times 3{{\text{e}}^{3x}}\) and \(RHS\) is \({3^0}{{\text{e}}^{3x}} + x{3^1}{{\text{e}}^{3x}}\) R1
as \({\text{LHS}} = {\text{RHS, }}P(1)\) is true
assume \(P(k)\) is true and attempt to prove \(P(k + 1)\) is true M1
assuming \(\frac{{{{\text{d}}^k}y}}{{{\text{d}}{x^k}}} = k{3^{k - 1}}{{\text{e}}^{3x}} + x{3^k}{{\text{e}}^{3x}}\)
\(\frac{{{{\text{d}}^{k + 1}}y}}{{{\text{d}}{x^{k + 1}}}} = \frac{{\text{d}}}{{{\text{d}}x}}\left( {\frac{{{{\text{d}}^k}y}}{{{\text{d}}{x^k}}}} \right)\) (M1)
\( = k{3^{k - 1}} \times 3{{\text{e}}^{3x}} + 1 \times {3^k}{{\text{e}}^{3x}} + x{3^k} \times 3{{\text{e}}^{3x}}\) A1
\( = (k + 1){3^k}{{\text{e}}^{3x}} + x{3^{k + 1}}{{\text{e}}^{3x}}\;\;\;\)(as required) A1
Note: Can award the A marks independent of the M marks
since \(P(1)\) is true and \(P(k)\) is true \( \Rightarrow P(k + 1)\) is true
then (by \(PMI\)), \(P(n)\) is true \((\forall n \in {\mathbb{Z}^ + })\) R1
Note: To gain last R1 at least four of the above marks must have been gained.
[7 marks]
\({{\text{e}}^{3x}} + x \times 3{{\text{e}}^{3x}} = 0 \Rightarrow 1 + 3x = 0 \Rightarrow x = - \frac{1}{3}\) M1A1
point is \(\left( { - \frac{1}{3},{\text{ }} - \frac{1}{{3{\text{e}}}}} \right)\) A1
EITHER
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 2 \times 3{{\text{e}}^{3x}} + x \times {3^2}{{\text{e}}^{3x}}\)
when \(x = - \frac{1}{3},{\text{ }}\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} > 0\) therefore the point is a minimum M1A1
OR

nature table shows point is a minimum M1A1
[5 marks]
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 2 \times 3{{\text{e}}^{3x}} + x \times {3^2}{{\text{e}}^{3x}}\) A1
\(2 \times 3{{\text{e}}^{3x}} + x \times {3^2}{{\text{e}}^{3x}} = 0 \Rightarrow 2 + 3x = 0 \Rightarrow x = - \frac{2}{3}\) M1A1
point is \(\left( { - \frac{2}{3},{\text{ }} - \frac{2}{{3{{\text{e}}^2}}}} \right)\) A1
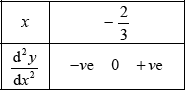
since the curvature does change (concave down to concave up) it is a point of inflection R1
Note: Allow \({3^{{\text{rd}}}}\) derivative is not zero at \( - \frac{2}{3}\)
[5 marks]
(general shape including asymptote and through origin) A1
showing minimum and point of inflection A1
Note: Only indication of position of answers to (c) and (d) required, not coordinates.
[2 marks]
Total [21 marks]
Examiners report
Well done.
The logic of an induction proof was not known well enough. Many candidates used what they had to prove rather than differentiating what they had assumed. They did not have enough experience in doing Induction proofs.
Good, some forgot to test for min/max, some forgot to give the \(y\) value.
Again quite good, some forgot to check for change in curvature and some forgot the \(y\) value.
Some accurate sketches, some had all the information from earlier parts but could not apply it. The asymptote was often missed.

