| Date | November 2013 | Marks available | 1 | Reference code | 13N.1.hl.TZ0.3 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | State | Question number | 3 | Adapted from | N/A |
Question
The diagram below shows a sketch of the graph of \(y = f(x)\).
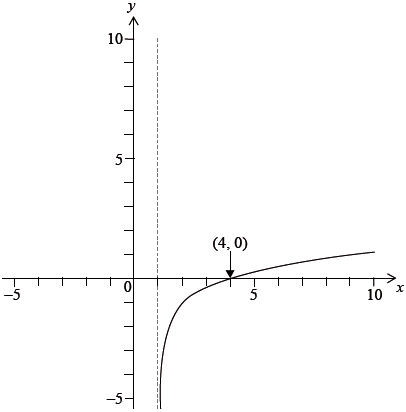
Sketch the graph of \(y = {f^{ - 1}}(x)\) on the same axes.
State the range of \({f^{ - 1}}\).
Given that \(f(x) = \ln (ax + b),{\text{ }}x > 1\), find the value of \(a\) and the value of \(b\).
Markscheme
(a) 
shape with y-axis intercept (0, 4) A1
Note: Accept curve with an asymptote at \(x = 1\) suggested.
correct asymptote \(y = 1\) A1
[2 marks]
range is \({f^{ - 1}}(x) > 1{\text{ (or }}\left] {1,{\text{ }}\infty } \right[)\) A1
Note: Also accept \(\left] {1,{\text{ 10}}} \right]\) or \(\left] {1,{\text{ 10}}} \right[\).
Note: Do not allow follow through from incorrect asymptote in (a).
[1 mark]
\((4,{\text{ }}0) \Rightarrow \ln (4a + b) = 0\) M1
\( \Rightarrow 4a + b = 1\) A1
asymptote at \(x = 1 \Rightarrow a + b = 0\) M1
\( \Rightarrow a = \frac{1}{3},{\text{ }}b = - \frac{1}{3}\) A1
[4 marks]
Examiners report
A number of candidates were able to answer a) and b) correctly but found part c) more challenging. Correct sketches for the inverse were seen, but with a few missing a horizontal asymptote. The range in part b) was usually seen correctly. In part c), only a small number of very good candidates were able to gain full marks. A large number used the point \((4,{\text{ 0)}}\) to form the equation \(4a + b = 1\) but were unable (or did not recognise the need) to use the asymptote to form a second equation.
A number of candidates were able to answer a) and b) correctly but found part c) more challenging. Correct sketches for the inverse were seen, but with a few missing a horizontal asymptote. The range in part b) was usually seen correctly. In part c), only a small number of very good candidates were able to gain full marks. A large number used the point \((4,{\text{ 0)}}\) to form the equation \(4a + b = 1\) but were unable (or did not recognise the need) to use the asymptote to form a second equation.
A number of candidates were able to answer a) and b) correctly but found part c) more challenging. Correct sketches for the inverse were seen, but with a few missing a horizontal asymptote. The range in part b) was usually seen correctly. In part c), only a small number of very good candidates were able to gain full marks. A large number used the point \((4,{\text{ 0)}}\) to form the equation \(4a + b = 1\) but were unable (or did not recognise the need) to use the asymptote to form a second equation.

