| Date | November 2017 | Marks available | 4 | Reference code | 17N.1.hl.TZ0.6 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Sketch | Question number | 6 | Adapted from | N/A |
Question
Sketch the graph of \(y = \frac{{1 - 3x}}{{x - 2}}\), showing clearly any asymptotes and stating the coordinates of any points of intersection with the axes.
Hence or otherwise, solve the inequality \(\left| {\frac{{1 - 3x}}{{x - 2}}} \right| < 2\).
Markscheme
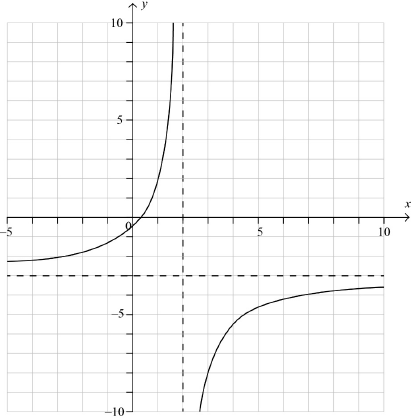
correct vertical asymptote A1
shape including correct horizontal asymptote A1
\(\left( {\frac{1}{3},{\text{ }}0} \right)\) A1
\(\left( {0,{\text{ }} - \frac{1}{2}} \right)\) A1
Note: Accept \(x = \frac{1}{3}\) and \(y = - \frac{1}{2}\) marked on the axes.
[4 marks]
METHOD 1
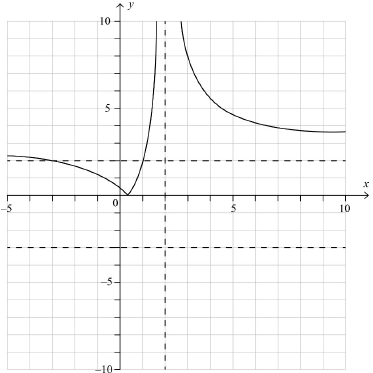
\(\frac{{1 - 3x}}{{x - 2}} = 2\) (M1)
\( \Rightarrow x = 1\) A1
\( - \left( {\frac{{1 - 3x}}{{x - 2}}} \right) = 2\) (M1)
Note: Award this M1 for the line above or a correct sketch identifying a second critical value.
\( \Rightarrow x = - 3\) A1
solution is \( - 3 < x < 1\) A1
METHOD 2
\(\left| {1 - 3x} \right| < 2\left| {x - 2} \right|,{\text{ }}x \ne 2\)
\(1 - 6x + 9{x^2} < 4({x^2} - 4x + 4)\) (M1)A1
\(1 - 6x + 9{x^2} < 4{x^2} - 16x + 16\)
\(5{x^2} + 10x - 15 < 0\)
\({x^2} + 2x - 3 < 0\) A1
\((x + 3)(x - 1) < 0\) (M1)
solution is \( - 3 < x < 1\) A1
METHOD 3
\( - 2 < \frac{{1 - 3x}}{{x - 2}} < 2\)
consider \(\frac{{1 - 3x}}{{x - 2}} < 2\) (M1)
Note: Also allow consideration of “>” or “=” for the awarding of the M mark.
recognition of critical value at \(x = 1\) A1
consider \( - 2 < \frac{{1 - 3x}}{{x - 2}}\) (M1)
Note: Also allow consideration of “>” or “=” for the awarding of the M mark.
recognition of critical value at \(x = - 3\) A1
solution is \( - 3 < x < 1\) A1
[5 marks]

