| Date | May 2014 | Marks available | 18 | Reference code | 14M.2.hl.TZ1.12 |
| Level | HL only | Paper | 2 | Time zone | TZ1 |
| Command term | Deduce, Find, Simplify, Sketch, and State | Question number | 12 | Adapted from | N/A |
Question
Let \(f(x) = \left| x \right| - 1\).
(a) The graph of \(y = g(x)\) is drawn below.
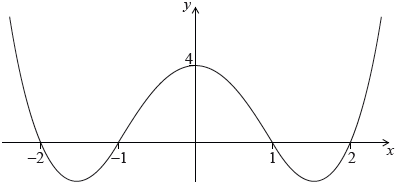
(i) Find the value of \((f \circ g)(1)\).
(ii) Find the value of \((f \circ g \circ g)(1)\).
(iii) Sketch the graph of \(y = (f \circ g)(x)\).
(b) (i) Sketch the graph of \(y = f(x)\).
(ii) State the zeros of f.
(c) (i) Sketch the graph of \(y = (f \circ f)(x)\).
(ii) State the zeros of \(f \circ f\).
(d) Given that we can denote \(\underbrace {f \circ f \circ f \circ \ldots \circ f}_{n{\text{ times}}}\) as \({f^n}\),
(i) find the zeros of \({f^3}\);
(ii) find the zeros of \({f^4}\);
(iii) deduce the zeros of \({f^8}\).
(e) The zeros of \({f^{2n}}\) are \({a_1},{\text{ }}{a_2},{\text{ }}{a_3},{\text{ }} \ldots {\text{, }}{a_N}\).
(i) State the relation between n and N;
(ii) Find, and simplify, an expression for \(\sum\limits_{r = 1}^N {\left| {{a_r}} \right|} \) in terms of n.
Markscheme
(a) (i) \(f(0) = - 1\) (M1)A1
(ii) \((f \circ g)(0) = f(4) = 3\) A1
(iii)
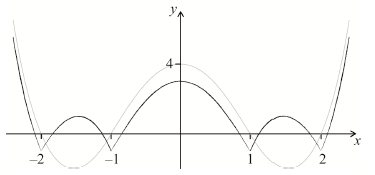 (M1)A1
(M1)A1
Note: Award M1 for evidence that the lower part of the graph has been reflected and A1 correct shape with y-intercept below 4.
[5 marks]
(b) (i)
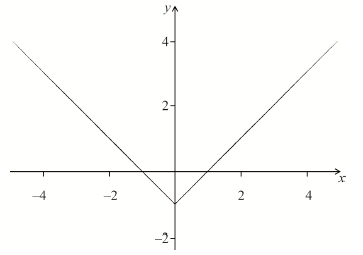 (M1)A1
(M1)A1
Note: Award M1 for any translation of \(y = \left| x \right|\).
(ii) \( \pm 1\) A1
Note: Do not award the A1 if coordinates given, but do not penalise in the rest of the question
[3 marks]
(c) (i)
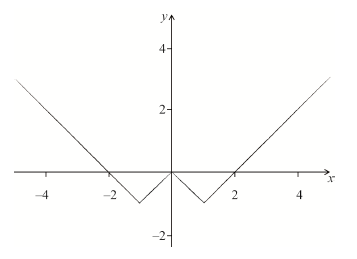 (M1)A1
(M1)A1
Note: Award M1 for evidence that lower part of (b) has been reflected in the x-axis and translated.
(ii) \(0,{\text{ }} \pm 2\) A1
[3 marks]
(d) (i) \( \pm 1,{\text{ }} \pm 3\) A1
(ii) \(0,{\text{ }} \pm 2,{\text{ }} \pm 4\) A1
(iii) \(0,{\text{ }} \pm 2,{\text{ }} \pm 4,{\text{ }} \pm 6,{\text{ }} \pm 8\) A1
[3 marks]
(e) (i) \({\text{(1, 3), (2, 5), }} \ldots \) (M1)
\(N = 2n + 1\) A1
(ii) Using the formula of the sum of an arithmetic series (M1)
EITHER
\(4(1 + 2 + 3 + \ldots + n) = \frac{4}{2}n(n + 1)\)
\( = 2n(n + 1)\) A1
OR
\(2(2 + 4 + 6 + \ldots + 2n) = \frac{2}{2}n(2n + 2)\)
\( = 2n(n + 1)\) A1
[4 marks]
Total [18 marks]

