| Date | May 2014 | Marks available | 4 | Reference code | 14M.2.hl.TZ2.7 |
| Level | HL only | Paper | 2 | Time zone | TZ2 |
| Command term | Sketch and Write down | Question number | 7 | Adapted from | N/A |
Question
The function f is defined as \(f(x) = - 3 + \frac{1}{{x - 2}},{\text{ }}x \ne 2\).
(i) Sketch the graph of \(y = f(x)\), clearly indicating any asymptotes and axes intercepts.
(ii) Write down the equations of any asymptotes and the coordinates of any axes intercepts.
Find the inverse function \({f^{ - 1}}\), stating its domain.
Markscheme
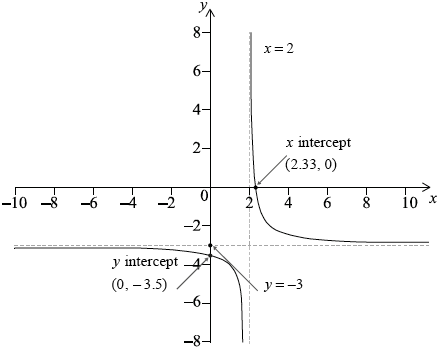A1A1A1
Note: Award A1 for correct shape, A1 for \(x = 2\) clearly stated and A1 for \(y = - 3\) clearly stated.
x intercept (2.33, 0) and y intercept (0, –3.5) A1
Note: Accept –3.5 and 2.33 (7/3) marked on the correct axes.
[4 marks]
\(x = - 3 + \frac{1}{{y - 2}}\) M1
Note: Award M1 for interchanging x and y (can be done at a later stage).
\(x + 3 = \frac{1}{{y - 2}}\)
\(y - 2 = \frac{1}{{x + 3}}\) M1
Note: Award M1 for attempting to make y the subject.
\({f^{ - 1}}(x) = 2 + \frac{1}{{x + 3}}\left( { = \frac{{2x + 7}}{{x + 3}}} \right),{\text{ }}x \ne - 3\) A1A1
Note: Award A1 only if \({f^{ - 1}}(x)\) is seen. Award A1 for the domain.
[4 marks]
