| Date | November 2015 | Marks available | 3 | Reference code | 15N.1.hl.TZ0.12 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Indicate and Sketch | Question number | 12 | Adapted from | N/A |
Question
Consider the function defined by \(f(x) = x\sqrt {1 - {x^2}} \) on the domain \( - 1 \le x \le 1\).
Show that \(f\) is an odd function.
Find \(f'(x)\).
Hence find the \(x\)-coordinates of any local maximum or minimum points.
Find the range of \(f\).
Sketch the graph of \(y = f(x)\) indicating clearly the coordinates of the \(x\)-intercepts and any local maximum or minimum points.
Find the area of the region enclosed by the graph of \(y = f(x)\) and the \(x\)-axis for \(x \ge 0\).
Show that \(\int_{ - 1}^1 {\left| {x\sqrt {1 - {x^2}} } \right|{\text{d}}x > \left| {\int_{ - 1}^1 {x\sqrt {1 - {x^2}} {\text{d}}x} } \right|} \).
Markscheme
\(f( - x) = ( - x)\sqrt {1 - {{( - x)}^2}} \) M1
\( = - x\sqrt {1 - {x^2}} \)
\( = - f(x)\) R1
hence \(f\) is odd AG
[2 marks]
\(f'(x) = x \bullet \frac{1}{2}{(1 - {x^2})^{ - \frac{1}{2}}} \bullet - 2x + {(1 - {x^2})^{\frac{1}{2}}}\) M1A1A1
[3 marks]
\(f'(x) = \sqrt {1 - {x^2}} - \frac{{{x^2}}}{{\sqrt {1 - {x^2}} }}\;\;\;\left( { = \frac{{1 - 2{x^2}}}{{\sqrt {1 - {x^2}} }}} \right)\) A1
Note: This may be seen in part (b).
Note: Do not allow FT from part (b).
\(f'(x) = 0 \Rightarrow 1 - 2{x^2} = 0\) M1
\(x = \pm \frac{1}{{\sqrt 2 }}\) A1
[3 marks]
\(y\)-coordinates of the Max Min Points are \(y = \pm \frac{1}{2}\) M1A1
so range of \(f(x)\) is \(\left[ { - \frac{1}{2},{\text{ }}\frac{1}{2}} \right]\) A1
Note: Allow FT from (c) if values of \(x\), within the domain, are used.
[3 marks]
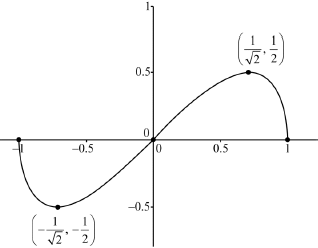
Shape: The graph of an odd function, on the given domain, s-shaped,
where the max(min) is the right(left) of \(0.5{\text{ }}( - 0.5)\) A1
\(x\)-intercepts A1
turning points A1
[3 marks]
\({\text{area}} = \int_0^1 {x\sqrt {1 - {x^2}} {\text{d}}x} \) (M1)
attempt at “backwards chain rule” or substitution M1
\( = - \frac{1}{2}\int_0^1 {( - 2x)\sqrt {1 - {x^2}} {\text{d}}x} \)
Note: Condone absence of limits for first two marks.
\( = \left[ {\frac{2}{3}{{(1 - {x^2})}^{\frac{3}{2}}} \bullet - \frac{1}{2}} \right]_0^1\) A1
\( = \left[ { - \frac{1}{3}{{(1 - {x^2})}^{\frac{3}{2}}}} \right]_0^1\)
\( = 0 - \left( { - \frac{1}{3}} \right) = \frac{1}{3}\) A1
[4 marks]
\(\int_{ - 1}^1 {\left| {x\sqrt {1 - {x^2}} } \right|{\text{d}}x > 0} \) R1
\(\left| {\int_{ - 1}^1 {x\sqrt {1 - {x^2}} {\text{d}}x} } \right| = 0\) R1
so \(\int_{ - 1}^1 {\left| {x\sqrt {1 - {x^2}} } \right|{\text{d}}x > \left| {\int_{ - 1}^1 {x\sqrt {1 - {x^2}} {\text{d}}x} } \right|} \) AG
[2 marks]
Total [20 marks]

