| Date | May 2011 | Marks available | 5 | Reference code | 11M.1.sl.TZ2.8 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Show that | Question number | 8 | Adapted from | N/A |
Question
The following diagram shows part of the graph of the function \(f(x) = 2{x^2}\) .
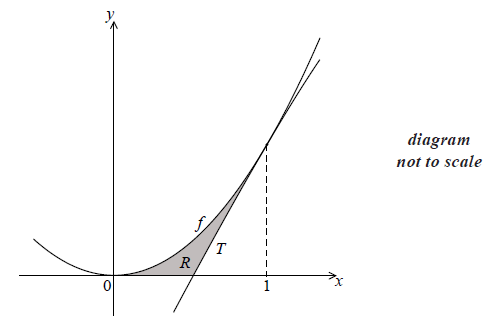
The line T is the tangent to the graph of f at \(x = 1\) .
Show that the equation of T is \(y = 4x - 2\) .
Find the x-intercept of T .
The shaded region R is enclosed by the graph of f , the line T , and the x-axis.
(i) Write down an expression for the area of R .
(ii) Find the area of R .
Markscheme
\(f(1) = 2\) (A1)
\(f'(x) = 4x\) A1
evidence of finding the gradient of f at \(x = 1\) M1
e.g. substituting \(x = 1\) into \(f'(x)\)
finding gradient of f at \(x = 1\) A1
e.g. \(f'(1) = 4\)
evidence of finding equation of the line M1
e.g. \(y - 2 = 4(x - 1)\) , \(2 = 4(1) + b\)
\(y = 4x - 2\) AG N0
[5 marks]
appropriate approach (M1)
e.g. \(4x - 2 = 0\)
\(x = \frac{1}{2}\) A1 N2
[2 marks]
(i) bottom limit \(x = 0\) (seen anywhere) (A1)
approach involving subtraction of integrals/areas (M1)
e.g. \(\int {f(x) - {\text{area of triangle}}} \) , \(\int {f - \int l } \)
correct expression A2 N4
e.g. \(\int_0^1 {2{x^2}{\rm{d}}x - } \int_{0.5}^1 {(4x - 2){\rm{d}}x} \) , \(\int_0^1 {f(x){\rm{d}}x - \frac{1}{2}} \) , \(\int_0^{0.5} {2{x^2}{\rm{d}}x} + \int_{0.5}^1 {(f(x) - (4x - 2)){\rm{d}}x} \)
(ii) METHOD 1 (using only integrals)
correct integration (A1)(A1)(A1)
\(\int {2{x^2}{\rm{d}}x} = \frac{{2{x^3}}}{3}\) , \(\int {(4x - 2){\rm{d}}x = } 2{x^2} - 2x\)
substitution of limits (M1)
e.g. \(\frac{1}{{12}} + \frac{2}{3} - 2 + 2 - \left( {\frac{1}{{12}} - \frac{1}{2} + 1} \right)\)
area = \(\frac{1}{6}\) A1 N4
METHOD 2 (using integral and triangle)
area of triangle = \(\frac{1}{2}\) (A1)
correct integration (A1)
\(\int {2{x^2}{\rm{d}}x = } \frac{{2{x^3}}}{3}\)
substitution of limits (M1)
e.g. \(\frac{2}{3}{(1)^3} - \frac{2}{3}{(0)^3}\) , \(\frac{2}{3} - 0\)
correct simplification (A1)
e.g. \(\frac{2}{3} - \frac{1}{2}\)
area = \(\frac{1}{6}\) A1 N4
[9 marks]
Examiners report
The majority of candidates seemed to know what was meant by the tangent to the graph in part (a), but there were many who did not fully show their work, which is of course necessary on a "show that" question. While many candidates knew they needed to find the derivative of f , some failed to substitute the given value of x in order to find the gradient of the tangent.
Part (b), finding the x-intercept, was answered correctly by nearly every candidate.
In part (c), most candidates struggled with writing an expression for the area of R . Many tried to use the difference of the two functions over the entire interval 0–1, not noticing that the area from 0–0.5 only required the use of function f . Many of these candidates were able to earn follow-through marks in the second part of (c) for their correct integration. There were a few candidates who successfully found the area under the line as the area of a triangle.

