| Date | November 2015 | Marks available | 5 | Reference code | 15N.1.sl.TZ0.10 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 10 | Adapted from | N/A |
Question
Let \(y = f(x)\), for \( - 0.5 \le \) x \( \le \) \(6.5\). The following diagram shows the graph of \(f'\), the derivative of \(f\).
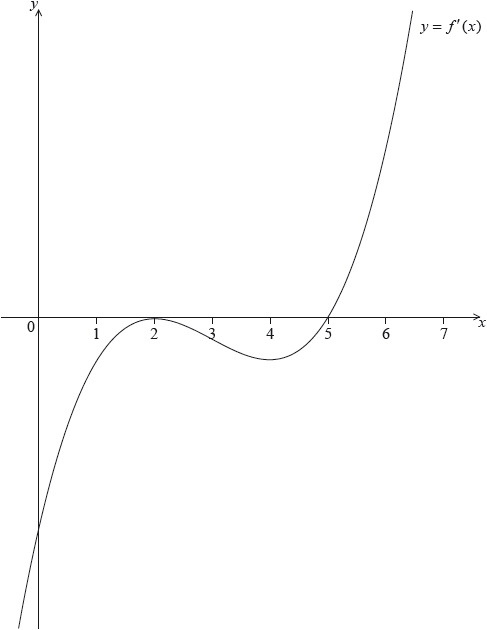
The graph of \(f'\) has a local maximum when \(x = 2\), a local minimum when \(x = 4\), and it crosses the \(x\)-axis at the point \((5,{\text{ }}0)\).
Explain why the graph of \(f\) has a local minimum when \(x = 5\).
Find the set of values of \(x\) for which the graph of \(f\) is concave down.
The following diagram shows the shaded regions \(A\), \(B\) and \(C\).
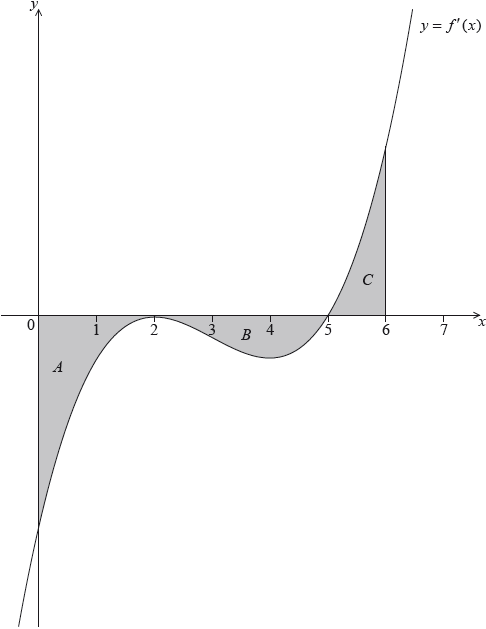
The regions are enclosed by the graph of \(f'\), the \(x\)-axis, the \(y\)-axis, and the line \(x = 6\).
The area of region \(A\) is 12, the area of region \(B\) is 6.75 and the area of region \(C\) is 6.75.
Given that \(f(0) = 14\), find \(f(6)\).
The following diagram shows the shaded regions \(A\), \(B\) and \(C\).

The regions are enclosed by the graph of \(f'\), the x-axis, the y-axis, and the line \(x = 6\).
The area of region \(A\) is 12, the area of region \(B\) is 6.75 and the area of region \(C\) is 6.75.
Let \(g(x) = {\left( {f(x)} \right)^2}\). Given that \(f'(6) = 16\), find the equation of the tangent to the graph of \(g\) at the point where \(x = 6\).
Markscheme
METHOD 1
\(f'(5) = 0\) (A1)
valid reasoning including reference to the graph of \(f'\) R1
eg\(\;\;\;f'\) changes sign from negative to positive at \(x = 5\), labelled sign chart for \(f'\)
so \(f\) has a local minimum at \(x = 5\) AG N0
Note: It must be clear that any description is referring to the graph of \(f'\), simply giving the conditions for a minimum without relating them to \(f'\) does not gain the R1.
METHOD 2
\(f'(5) = 0\) A1
valid reasoning referring to second derivative R1
eg\(\;\;\;f''(5) > 0\)
so \(f\) has a local minimum at \(x = 5\) AG N0
[2 marks]
attempt to find relevant interval (M1)
eg\(\;\;\;f'\) is decreasing, gradient of \(f'\) is negative, \(f'' < 0\)
\(2 < x < 4\;\;\;\)(accept “between 2 and 4”) A1 N2
Notes: If no other working shown, award M1A0 for incorrect inequalities such as \(2 \le \) \(x\) \( \le \) 4, or “from 2 to 4”
[2 marks]
METHOD 1 (one integral)
correct application of Fundamental Theorem of Calculus (A1)
eg\(\;\;\;\int_0^6 {f'(x){\text{d}}x = } f(6) - f(0),{\text{ }}f(6) = 14 + \int_0^6 {f'(x){\text{d}}x} \)
attempt to link definite integral with areas (M1)
eg\(\;\;\;\int_0^6 {f'(x){\text{d}}x = - 12 - 6.75 + 6.75,{\text{ }}\int_0^6 {f'(x){\text{d}}x = {\text{Area }}A + {\text{Area }}B + {\text{ Area }}C} } \)
correct value for \(\int_0^6 {f'(x){\text{d}}x} \) (A1)
eg\(\;\;\;\int_0^6 {f'(x){\text{d}}x} = - 12\)
correct working A1
eg\(\;\;\;f(6) - 14 = - 12,{\text{ }}f(6) = - 12 + f(0)\)
\(f(6) = 2\) A1 N3
METHOD 2 (more than one integral)
correct application of Fundamental Theorem of Calculus (A1)
eg\(\;\;\;\int_0^2 {f'(x){\text{d}}x} = f(2) - f(0),{\text{ }}f(2) = 14 + \int_0^2 {f'(x)} \)
attempt to link definite integrals with areas (M1)
eg\(\;\;\;\int_0^2 {f'(x){\text{d}}x} = 12,{\text{ }}\int_2^5 {f'(x){\text{d}}x = - 6.75} ,{\text{ }}\int_0^6 {f'(x)} = 0\)
correct values for integrals (A1)
eg\(\;\;\;\int_0^2 {f'(x){\text{d}}x} = - 12,{\text{ }}\int_5^2 {f'(x)} {\text{d}}x = 6.75,{\text{ }}f(6) - f(2) = 0\)
one correct intermediate value A1
eg\(\;\;\;f(2) = 2,{\text{ }}f(5) = - 4.75\)
\(f(6) = 2\) A1 N3
[5 marks]
correct calculation of \(g(6)\) (seen anywhere) A1
eg\(\;\;\;{2^2},{\text{ }}g(6) = 4\)
choosing chain rule or product rule (M1)
eg\(\;\;\;g'\left( {f(x)} \right)f'(x),{\text{ }}\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{{\text{d}}y}}{{{\text{d}}u}} \times \frac{{{\text{d}}u}}{{{\text{d}}x}},{\text{ }}f(x)f'(x) + f'(x)f(x)\)
correct derivative (A1)
eg\(\;\;\;g'(x) = 2f(x)f'(x),{\text{ }}f(x)f'(x) + f'(x)f(x)\)
correct calculation of \(g'(6)\) (seen anywhere) A1
eg\(\;\;\;2(2)(16),{\text{ }}g'(6) = 64\)
attempt to substitute their values of \(g'(6)\) and \(g(6)\) (in any order) into equation of a line (M1)
eg\(\;\;\;{2^2} = (2 \times 2 \times 16)6 + b,{\text{ }}y - 6 = 64(x - 4)\)
correct equation in any form A1 N2
eg\(\;\;\;y - 4 = 64(x - 6),{\text{ }}y = 64x - 380\)
[6 marks]
[Total 15 marks]

