| Date | May 2016 | Marks available | 6 | Reference code | 16M.1.sl.TZ2.10 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Show that | Question number | 10 | Adapted from | N/A |
Question
The following diagram shows the graph of \(f(x) = 2x\sqrt {{a^2} - {x^2}} \), for \( - 1 \leqslant x \leqslant a\), where \(a > 1\).
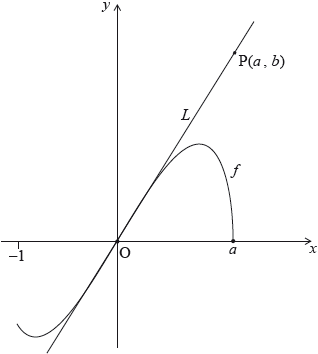
The line \(L\) is the tangent to the graph of \(f\) at the origin, O. The point \({\text{P}}(a,{\text{ }}b)\) lies on \(L\).
The point \({\text{Q}}(a,{\text{ }}0)\) lies on the graph of \(f\). Let \(R\) be the region enclosed by the graph of \(f\) and the \(x\)-axis. This information is shown in the following diagram.
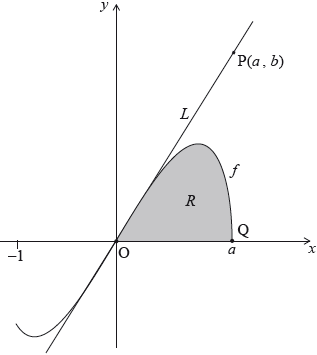
Let \({A_R}\) be the area of the region \(R\).
(i) Given that \(f'(x) = \frac{{2{a^2} - 4{x^2}}}{{\sqrt {{a^2} - {x^2}} }}\), for \( - 1 \leqslant x < a\), find the equation of \(L\).
(ii) Hence or otherwise, find an expression for \(b\) in terms of \(a\).
Show that \({A_R} = \frac{2}{3}{a^3}\).
Let \({A_T}\) be the area of the triangle OPQ. Given that \({A_T} = k{A_R}\), find the value of \(k\).
Markscheme
(i) recognizing the need to find the gradient when \(x = 0\) (seen anywhere) R1
eg\(\,\,\,\,\,\)\(f'(0)\)
correct substitution (A1)
\(f'(0) = \frac{{2{a^2} - 4(0)}}{{\sqrt {{a^2} - 0} }}\)
\(f'(0) = 2a\) (A1)
correct equation with gradient 2\(a\) (do not accept equations of the form \(L = 2ax\)) A1 N3
eg\(\,\,\,\,\,\)\(y = 2ax,{\text{ }}y - b = 2a(x - a),{\text{ }}y = 2ax - 2{a^2} + b\)
(ii) METHOD 1
attempt to substitute \(x = a\) into their equation of \(L\) (M1)
eg\(\,\,\,\,\,\)\(y = 2a \times a\)
\(b = 2{a^2}\) A1 N2
METHOD 2
equating gradients (M1)
eg\(\,\,\,\,\,\)\(\frac{b}{a} = 2a\)
\(b = 2{a^2}\) A1 N2
[6 marks]
METHOD 1
recognizing that area \( = \int_0^a {f(x){\text{d}}x} \) (seen anywhere) R1
valid approach using substitution or inspection (M1)
eg\(\,\,\,\,\,\)\(\int {2x\sqrt u {\text{d}}x,{\text{ }}u = {a^2} - {x^2},{\text{ d}}u = - 2x{\text{d}}x,{\text{ }}\frac{2}{3}{{({a^2} - {x^2})}^{\frac{3}{2}}}} \)
correct working (A1)
eg\(\,\,\,\,\,\)\(\int {2x\sqrt {{a^2} - {x^2}} {\text{d}}x = \int { - \sqrt u {\text{d}}u} } \)
\(\int { - \sqrt u {\text{d}}u = - \frac{{{u^{\frac{3}{2}}}}}{{\frac{3}{2}}}} \) (A1)
\(\int {f(x){\text{d}}x = - \frac{2}{3}{{({a^2} - {x^2})}^{\frac{3}{2}}} + c} \) (A1)
substituting limits and subtracting A1
eg\(\,\,\,\,\,\)\({A_R} = - \frac{2}{3}{({a^2} - {a^2})^{\frac{3}{2}}} + \frac{2}{3}{({a^2} - 0)^{\frac{3}{2}}},{\text{ }}\frac{2}{3}{({a^2})^{\frac{3}{2}}}\)
\({A_R} = \frac{2}{3}{a^3}\) AG N0
METHOD 2
recognizing that area \( = \int_0^a {f(x){\text{d}}x} \) (seen anywhere) R1
valid approach using substitution or inspection (M1)
eg\(\,\,\,\,\,\)\(\int {2x\sqrt u {\text{d}}x,{\text{ }}u = {a^2} - {x^2},{\text{ d}}u = - 2x{\text{d}}x,{\text{ }}\frac{2}{3}{{({a^2} - {x^2})}^{\frac{3}{2}}}} \)
correct working (A1)
eg\(\,\,\,\,\,\)\(\int {2x\sqrt {{a^2} - {x^2}} {\text{d}}x = \int { - \sqrt u {\text{d}}u} } \)
\(\int { - \sqrt u {\text{d}}u = - \frac{{{u^{\frac{3}{2}}}}}{{\frac{3}{2}}}} \) (A1)
new limits for u (even if integration is incorrect) (A1)
eg\(\,\,\,\,\,\)\(u = 0{\text{ and }}u = {a^2},{\text{ }}\int_0^{{a^2}} {{u^{\frac{1}{2}}}{\text{d}}u,{\text{ }}\left[ { - \frac{2}{3}{u^{\frac{3}{2}}}} \right]} _{{a^2}}^0\)
substituting limits and subtracting A1
eg\(\,\,\,\,\,\)\({A_R} = - \left( {0 - \frac{2}{3}{a^3}} \right),{\text{ }}\frac{2}{3}{({a^2})^{\frac{3}{2}}}\)
\({A_R} = \frac{2}{3}{a^3}\) AG N0
[6 marks]
METHOD 1
valid approach to find area of triangle (M1)
eg\(\,\,\,\,\,\)\(\frac{1}{2}({\text{OQ)(PQ), }}\frac{1}{2}ab\)
correct substitution into formula for \({A_T}\) (seen anywhere) (A1)
eg\(\,\,\,\,\,\)\({A_T} = \frac{1}{2} \times a \times 2{a^2},{\text{ }}{a^3}\)
valid attempt to find \(k\) (must be in terms of \(a\)) (M1)
eg\(\,\,\,\,\,\)\({a^3} = k\frac{2}{3}{a^3},{\text{ }}k = \frac{{{a^3}}}{{\frac{2}{3}{a^3}}}\)
\(k = \frac{3}{2}\) A1 N2
METHOD 2
valid approach to find area of triangle (M1)
eg\(\,\,\,\,\,\)\(\int_0^a {(2ax){\text{d}}x} \)
correct working (A1)
eg\(\,\,\,\,\,\)\([a{x^2}]_0^a,{\text{ }}{a^3}\)
valid attempt to find \(k\) (must be in terms of \(a\)) (M1)
eg\(\,\,\,\,\,\)\({a^3} = k\frac{2}{3}{a^3},{\text{ }}k = \frac{{{a^3}}}{{\frac{2}{3}{a^3}}}\)
\(k = \frac{3}{2}\) A1 N2
[4 marks]
Examiners report
As is typically the case with question 10, this proved to be quite a challenging question for many candidates. In part (a), while many candidates seemed to recognize that there was some relationship between the given derivative and the gradient of the tangent line, most did not substitute zero for the \(x\)-value, and were unable to find the correct gradient of the line.
In part (b), nearly every candidate understood that the area was equal to the integral of \(f\) from 0 to \(a\), very few were able to integrate correctly using either substitution or inspection. Many candidates did not even attempt to integrate, stopping after writing the integral expression.
In part (c), most candidates started with a correct expression for the area of the triangle such as \(\frac{{ab}}{2}\). However, very few were able to substitute their expression for \(b\) from part (a)(ii), and therefore did not find a value for \(k\).

