| Date | May 2013 | Marks available | 3 | Reference code | 13M.1.sl.TZ2.7 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find | Question number | 7 | Adapted from | N/A |
Question
The following is the graph of a function \(f\) , for \(0 \le x \le 6\) .
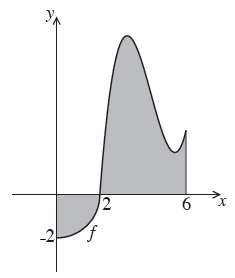
The first part of the graph is a quarter circle of radius \(2\) with centre at the origin.
(a) Find \(\int_0^2 {f(x){\rm{d}}x} \) .
(b) The shaded region is enclosed by the graph of \(f\) , the \(x\)-axis, the \(y\)-axis and the line \(x = 6\) . The area of this region is \(3\pi \) .
Find \(\int_2^6 {f(x){\rm{d}}x} \) .
Find \(\int_0^2 {f(x){\rm{d}}x} \) .
The shaded region is enclosed by the graph of \(f\) , the \(x\)-axis, the \(y\)-axis and the line \(x = 6\) . The area of this region is \(3\pi \) .
Find \(\int_2^6 {f(x){\rm{d}}x} \) .
Markscheme
(a) attempt to find quarter circle area (M1)
eg \(\frac{1}{4}(4\pi )\) , \(\frac{{\pi {r^2}}}{4}\) , \(\int_0^2 {\sqrt {4 - {x^2}{\rm{d}}x} } \)
area of region \( = \pi \) (A1)
\(\int_0^2 {f(x){\rm{d}}x = - \pi } \) A2 N3
[4 marks]
(b) attempted set up with both regions (M1)
eg \({\text{shaded area}} - {\text{quarter circle}}\) , \(3\pi - \pi \) , \(3\pi - \int_0^2 {f = \int_2^6 f } \)
\(\int_2^6 {f(x){\rm{d}}x = 2\pi } \) A2 N2
[3 marks]
Total [7 marks]
attempt to find quarter circle area (M1)
eg \(\frac{1}{4}(4\pi )\) , \(\frac{{\pi {r^2}}}{4}\) , \(\int_0^2 {\sqrt {4 - {x^2}{\rm{d}}x} } \)
area of region \( = \pi \) (A1)
\(\int_0^2 {f(x){\rm{d}}x = - \pi } \) A2 N3
[4 marks]
attempted set up with both regions (M1)
eg \({\text{shaded area}} - {\text{quarter circle}}\) , \(3\pi - \pi \) , \(3\pi - \int_0^2 {f = \int_2^6 f } \)
\(\int_2^6 {f(x){\rm{d}}x = 2\pi } \) A2 N2
[3 marks]
Total [7 marks]
Examiners report
There was a minor error on the diagram, where the point on the \(y\)-axis was labelled \(2\) (to indicate the length of the radius), rather than \( - 2\). Examiners were instructed to notify the IB assessment centre of any candidates adversely affected. Candidate scripts did not indicate any adverse effect.
While most candidates were able to correctly find the area of the quarter circle in part (a), very few considered that the value of the definite integral is negative for the part of the function below the \(x\)-axis. In part (b), most went on to earn full marks by subtracting the area of the quarter circle from \(3 \pi\).
Candidates who did not understand the connection between area and the value of the integral often tried to find a function to integrate. These candidates were not successful using this method.
There was a minor error on the diagram, where the point on the \(y\)-axis was labelled \(2\) (to indicate the length of the radius), rather than \( - 2\). Examiners were instructed to notify the IB assessment centre of any candidates adversely affected. Candidate scripts did not indicate any adverse effect.
While most candidates were able to correctly find the area of the quarter circle in part (a), very few considered that the value of the definite integral is negative for the part of the function below the \(x\)-axis. In part (b), most went on to earn full marks by subtracting the area of the quarter circle from \(3 \pi\).
Candidates who did not understand the connection between area and the value of the integral often tried to find a function to integrate. These candidates were not successful using this method.
There was a minor error on the diagram, where the point on the \(y\)-axis was labelled \(2\) (to indicate the length of the radius), rather than \( - 2\). Examiners were instructed to notify the IB assessment centre of any candidates adversely affected. Candidate scripts did not indicate any adverse effect.
While most candidates were able to correctly find the area of the quarter circle in part (a), very few considered that the value of the definite integral is negative for the part of the function below the \(x\)-axis. In part (b), most went on to earn full marks by subtracting the area of the quarter circle from \(3 \pi\).
Candidates who did not understand the connection between area and the value of the integral often tried to find a function to integrate. These candidates were not successful using this method.

