| Date | May 2012 | Marks available | 3 | Reference code | 12M.1.sl.TZ2.8 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find | Question number | 8 | Adapted from | N/A |
Question
The following diagram shows the graph of a quadratic function f , for \(0 \le x \le 4\) .
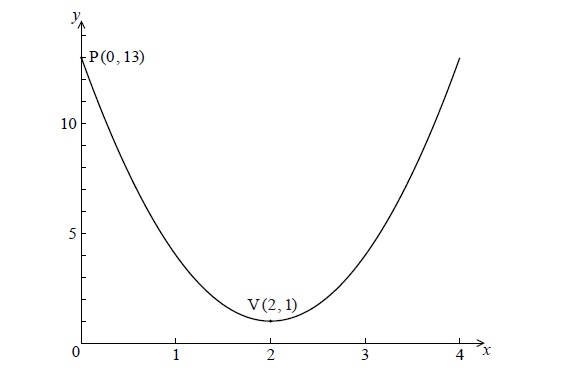
The graph passes through the point P(0, 13) , and its vertex is the point V(2, 1) .
The function can be written in the form \(f(x) = a{(x - h)^2} + k\) .
(i) Write down the value of h and of k .
(ii) Show that \(a = 3\) .
Find \(f(x)\) , giving your answer in the form \(A{x^2} + Bx + C\) .
Calculate the area enclosed by the graph of f , the x-axis, and the lines \(x = 2\) and \(x = 4\) .
Markscheme
(i) \(h = 2\) , \(k = 1\) A1A1 N2
(ii) attempt to substitute coordinates of any point (except the vertex) on the graph into f M1
e.g. \(13 = a{(0 - 2)^2} + 1\)
working towards solution A1
e.g. \(13 = 4a + 1\)
\(a = 3\) AG N0
[4 marks]
attempting to expand their binomial (M1)
e.g. \(f(x) = 3({x^2} - 2 \times 2x + 4) + 1\) , \({(x - 2)^2} = {x^2} - 4x + 4\)
correct working (A1)
e.g. \(f(x) = 3{x^2} - 12x + 12 + 1\)
\(f(x) = 3{x^2} - 12x + 13\) (accept \(A = 3\) , \(B = - 12\) , \(C = 13\) ) A1 N2
[3 marks]
METHOD 1
integral expression (A1)
e.g. \(\int_2^4 {(3{x^2}} - 12x + 13)\) , \(\int {f{\rm{d}}x} \)
\({\rm{Area}} = [{x^3} - 6{x^2} + 13x]_2^4\) A1A1A1
Note: Award A1 for \({x^3}\) , A1 for \( - 6{x^2}\) , A1 for \(13x\) .
correct substitution of correct limits into their expression A1A1
e.g. \(({4^3} - 6 \times {4^2} + 13 \times 4) - ({2^3} - 6 \times {2^2} + 13 \times 2)\) , \(64 - 96 + 52 - (8 - 24 + 26)\)
Note: Award A1 for substituting 4, A1 for substituting 2.
correct working (A1)
e.g. \(64 - 96 + 52 - 8 + 24 - 26,20 - 10\)
\({\rm{Area}} = 10\) A1 N3
[8 marks]
METHOD 2
integral expression (A1)
e.g. \(\int_2^4 {(3{{(x - 2)}^2}} + 1)\) , \(\int {f{\rm{d}}x} \)
\({\rm{Area}} = [{(x - 2)^3} + x]_2^4\) A2A1
Note: Award A2 for \({(x - 2)^3}\) , A1 for \(x\) .
correct substitution of correct limits into their expression A1A1
e.g. \({(4 - 2)^3} + 4 - [{(2 - 2)^3} + 2]\) , \({2^3} + 4 - ({0^3} + 2)\) , \({2^3} + 4 - 2\)
Note: Award A1 for substituting 4, A1 for substituting 2.
correct working (A1)
e.g. \(8 + 4 - 2\)
\({\rm{Area}} = 10\) A1 N3
[8 marks]
METHOD 3
recognizing area from 0 to 2 is same as area from 2 to 4 (R1)
e.g. sketch, \(\int_2^4 {f = \int_0^2 f } \)
integral expression (A1)
e.g. \(\int_0^2 {(3{x^2}} - 12x + 13)\) , \(\int {f{\rm{d}}x} \)
\({\rm{Area}} = [{x^3} - 6{x^2} + 13x]_0^2\) A1A1A1
Note: Award A1 for \({x^3}\) , A1 for \( - 6{x^2}\) , A1 for \(13x\) .
correct substitution of correct limits into their expression A1(A1)
e.g. \(({2^3} - 6 \times {2^2} + 13 \times 2) - ({0^3} - 6 \times {0^2} + 13 \times 0)\) , \(8 - 24 + 26\)
Note: Award A1 for substituting 2, (A1) for substituting 0.
\({\rm{Area}} = 10\) A1 N3
[8 marks]
Examiners report
In part (a), nearly all the candidates recognized that h and k were the coordinates of the vertex of the parabola, and most were able to successfully show that \(a = 3\) . Unfortunately, a few candidates did not understand the "show that" command, and simply verified that \(a = 3\) would work, rather than showing how to find \(a = 3\) .
In part (b), most candidates were able to find \(f(x)\) in the required form. For a few candidates, algebraic errors kept them from finding the correct function, even though they started with correct values for a, h and k.
In part (c), nearly all candidates knew that they needed to integrate to find the area, but errors in integration, and algebraic and arithmetic errors prevented many from finding the correct area.

