| Date | November 2016 | Marks available | 4 | Reference code | 16N.2.sl.TZ0.9 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find and Hence | Question number | 9 | Adapted from | N/A |
Question
A particle P starts from a point A and moves along a horizontal straight line. Its velocity \(v{\text{ cm}}\,{{\text{s}}^{ - 1}}\) after \(t\) seconds is given by
\[v(t) = \left\{ {\begin{array}{*{20}{l}} { - 2t + 2,}&{{\text{for }}0 \leqslant t \leqslant 1} \\ {3\sqrt t + \frac{4}{{{t^2}}} - 7,}&{{\text{for }}1 \leqslant t \leqslant 12} \end{array}} \right.\]
The following diagram shows the graph of \(v\).
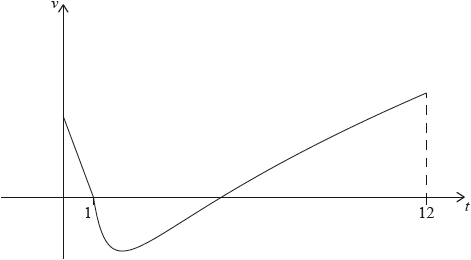
P is at rest when \(t = 1\) and \(t = p\).
When \(t = q\), the acceleration of P is zero.
Find the initial velocity of \(P\).
Find the value of \(p\).
(i) Find the value of \(q\).
(ii) Hence, find the speed of P when \(t = q\).
(i) Find the total distance travelled by P between \(t = 1\) and \(t = p\).
(ii) Hence or otherwise, find the displacement of P from A when \(t = p\).
Markscheme
valid attempt to substitute \(t = 0\) into the correct function (M1)
eg\(\,\,\,\,\,\)\( - 2(0) + 2\)
2 A1 N2
[2 marks]
recognizing \(v = 0\) when P is at rest (M1)
5.21834
\(p = 5.22{\text{ }}({\text{seconds}})\) A1 N2
[2 marks]
(i) recognizing that \(a = v'\) (M1)
eg\(\,\,\,\,\,\)\(v' = 0\), minimum on graph
1.95343
\(q = 1.95\) A1 N2
(ii) valid approach to find their minimum (M1)
eg\(\,\,\,\,\,\)\(v(q),{\text{ }} - 1.75879\), reference to min on graph
1.75879
speed \( = 1.76{\text{ }}(c\,{\text{m}}\,{{\text{s}}^{ - 1}})\) A1 N2
[4 marks]
(i) substitution of correct \(v(t)\) into distance formula, (A1)
eg\(\,\,\,\,\,\)\(\int_1^p {\left| {3\sqrt t + \frac{4}{{{t^2}}} - 7} \right|{\text{d}}t,{\text{ }}\left| {\int {3\sqrt t + \frac{4}{{{t^2}}} - 7{\text{d}}t} } \right|} \)
4.45368
distance \( = 4.45{\text{ }}({\text{cm}})\) A1 N2
(ii) displacement from \(t = 1\) to \(t = p\) (seen anywhere) (A1)
eg\(\,\,\,\,\,\)\( - 4.45368,{\text{ }}\int_1^p {\left( {3\sqrt t + \frac{4}{{{t^2}}} - 7} \right){\text{d}}t} \)
displacement from \(t = 0\) to \(t = 1\) (A1)
eg\(\,\,\,\,\,\)\(\int_0^1 {( - 2t + 2){\text{d}}t,{\text{ }}0.5 \times 1 \times 2,{\text{ 1}}} \)
valid approach to find displacement for \(0 \leqslant t \leqslant p\) M1
eg\(\,\,\,\,\,\)\(\int_0^1 {( - 2t + 2){\text{d}}t + \int_1^p {\left( {3\sqrt t + \frac{4}{{{t^2}}} - 7} \right){\text{d}}t,{\text{ }}\int_0^1 {( - 2t + 2){\text{d}}t - 4.45} } } \)
\( - 3.45368\)
displacement \( = - 3.45{\text{ }}({\text{cm}})\) A1 N2
[6 marks]

