| Date | May 2015 | Marks available | 8 | Reference code | 15M.1.sl.TZ1.7 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find | Question number | 7 | Adapted from | N/A |
Question
Let \(f(x) = \cos x\), for \(0\) \(\le \) \(x\) \( \le \) \(2\pi \). The following diagram shows the graph of \(f\).
There are \(x\)-intercepts at \(x = \frac{\pi }{2},{\text{ }}\frac{{3\pi }}{2}\).
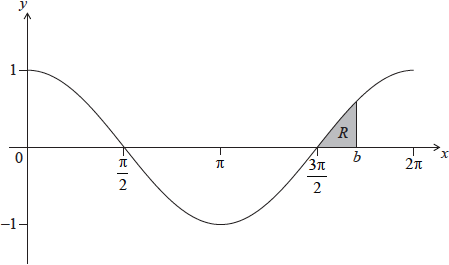
The shaded region \(R\) is enclosed by the graph of \(f\), the line \(x = b\), where \(b > \frac{{3\pi }}{2}\), and the \(x\)-axis. The area of \(R\) is \(\left( {1 - \frac{{\sqrt 3 }}{2}} \right)\). Find the value of \(b\).
Markscheme
attempt to set up integral (accept missing or incorrect limits and missing \({\text{d}}x\)) M1
eg\(\;\;\;\int_{\frac{{3\pi }}{2}}^b {\cos x{\text{d}}x,{\text{ }}\int_a^b {\cos x{\text{d}}x,{\text{ }}\int_{\frac{{3\pi }}{2}}^b {f{\text{d}}x,{\text{ }}\int {\cos x} } } } \)
correct integration (accept missing or incorrect limits) (A1)
eg\(\;\;\;[\sin x]_{\frac{{3\pi }}{2}}^b,{\text{ }}\sin x\)
substituting correct limits into their integrated function and subtracting (in any order) (M1)
eg\(\;\;\;\sin b - \sin \left( {\frac{{3\pi }}{2}} \right),{\text{ }}\sin \left( {\frac{{3\pi }}{2}} \right) - \sin b\)
\(\sin \left( {\frac{{3\pi }}{2}} \right) = - 1\;\;\;\)(seen anywhere) (A1)
setting their result from an integrated function equal to \(\left( {1 - \frac{{\sqrt 3 }}{2}} \right)\) M1
eg\(\;\;\;\sin b = - \frac{{\sqrt 3 }}{2}\)
evaluating \({\sin ^{ - 1}}\left( {\frac{{\sqrt 3 }}{2}} \right) = \frac{\pi }{3}\) or \({\sin ^{ - 1}}\left( { - \frac{{\sqrt 3 }}{2}} \right) = - \frac{\pi }{3}\) (A1)
eg\(\;\;\;b = \frac{\pi }{3},{\text{ }} - 60^\circ \)
identifying correct value (A1)
eg\(\;\;\;2\pi - \frac{\pi }{3},{\text{ }}360 - 60\)
\(b = \frac{{5\pi }}{3}\) A1 N3
[8 marks]
Examiners report
Most candidates recognised that a definite integral was required and many were able to set up a correct equation. Incorrect integration leading to \( - \sin x\) was quite common and poor notation was frequently seen. Some candidates appeared to guess their value from the graph, showing little supporting work.

