| Date | November 2011 | Marks available | 4 | Reference code | 11N.1.sl.TZ0.10 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 10 | Adapted from | N/A |
Question
Let \(f(x) = \frac{1}{4}{x^2} + 2\) . The line L is the tangent to the curve of f at (4, 6) .
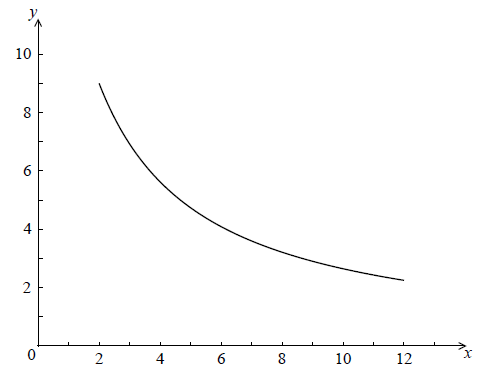
Let \(g(x) = \frac{{90}}{{3x + 4}}\) , for \(2 \le x \le 12\) . The following diagram shows the graph of g .
Find the equation of L .
Find the area of the region enclosed by the curve of g , the x-axis, and the lines \(x = 2\) and \(x = 12\) . Give your answer in the form \(a\ln b\) , where \(a,b \in \mathbb{Z}\) .
The graph of g is reflected in the x-axis to give the graph of h . The area of the region enclosed by the lines L , \(x = 2\) , \(x = 12\) and the x-axis is 120 \(120{\text{ c}}{{\text{m}}^2}\) .
Find the area enclosed by the lines L , \(x = 2\) , \(x = 12\) and the graph of h .
Markscheme
finding \(f'(x) = \frac{1}{2}x\) A1
attempt to find \(f'(4)\) (M1)
correct value \(f'(4) = 2\) A1
correct equation in any form A1 N2
e.g. \(y - 6 = 2(x - 4)\) , \(y = 2x - 2\)
[4 marks]
\({\rm{area}} = \int_2^{12} {\frac{{90}}{{3x + 4}}} {\rm{d}}x\)
correct integral A1A1
e.g. \(30\ln (3x + 4)\)
substituting limits and subtracting (M1)
e.g. \(30\ln (3 \times 12 + 4) - 30\ln (3 \times 2 + 4)\) , \(30\ln 40 - 30\ln 10\)
correct working (A1)
e.g. \(30(\ln 40 - \ln 10)\)
correct application of \(\ln b - \ln a\) (A1)
e.g. \(30\ln \frac{{40}}{{10}}\)
\({\rm{area}} = 30\ln 4\) A1 N4
[6 marks]
valid approach (M1)
e.g. sketch, area h = area g , 120 + their answer from (b)
\({\rm{area}} = 120 + 30\ln 4\) A2 N3
[3 marks]
Examiners report
While most candidates answered part (a) correctly, finding the equation of the tangent, there were some who did not consider the value of their derivative when \(x = 4\) .
In part (b), most candidates knew that they needed to integrate to find the area, but errors in integration, and misapplication of the rules of logarithms kept many from finding the correct area.
In part (c), it was clear that a significant number of candidates understood the idea of the reflected function, and some recognized that the integral was the negative of the integral from part (b), but only a few recognized the relationship between the areas. Many thought the area between h and the x-axis was 120.

