| Date | May 2008 | Marks available | 6 | Reference code | 08M.2.sl.TZ2.8 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find, Show that, and Write down | Question number | 8 | Adapted from | N/A |
Question
The following graph shows the depth of water, y metres , at a point P, during one day. The time t is given in hours, from midnight to noon.
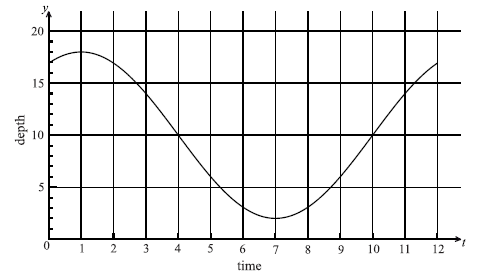
Use the graph to write down an estimate of the value of t when
(i) the depth of water is minimum;
(ii) the depth of water is maximum;
(iii) the depth of the water is increasing most rapidly.
The depth of water can be modelled by the function \(y = \cos A(B(t - 1)) + C\) .
(i) Show that \(A = 8\) .
(ii) Write down the value of C.
(iii) Find the value of B.
A sailor knows that he cannot sail past P when the depth of the water is less than 12 m . Calculate the values of t between which he cannot sail past P.
Markscheme
(i) 7 A1 N1
(ii) 1 A1 N1
(iii) 10 A1 N1
[3 marks]
(i) evidence of appropriate approach M1
e.g. \(A = \frac{{18 - 2}}{2}\)
\(A = 8\) AG N0
(ii) \(C = 10\) A2 N2
(iii) METHOD 1
\({\text{period}} = 12\) (A1)
evidence of using \(B \times {\rm{period}} = 2\pi \) (accept \(360^\circ \) ) (M1)
e.g. \(12 = \frac{{2\pi }}{B}\)
\(B = \frac{\pi }{6}\) (accept 0.524 or 30) A1 N3
METHOD 2
evidence of substituting (M1)
e.g. \(10 = 8\cos 3B + 10\)
simplifying (A1)
e.g. \(\cos 3B = 0\) \(\left( {3B = \frac{\pi }{2}} \right)\)
\(B = \frac{\pi }{6}\) (accept 0.524 or 30) A1 N3
[6 marks]
correct answers A1A1
e.g. \(t = 3.52\) , \(t = 10.5\) , between 03:31 and 10:29 (accept 10:30) N2
[2 marks]
Examiners report
For part (a), most candidates correctly used the graph to identify the times of maximum and minimum depth. Most failed to consider that the depth of water is increasing most rapidly at a point of inflexion and often answered with the interval \(t = 9\) to \(t = 11\) . A few candidates answered with the depth instead of time, misinterpreting which axis to consider.
A substantial number of candidates showed difficulty finding parameters of a trigonometric function with many only making superficial attempts at part (b), often leaving it blank entirely.
Some divided \(2\pi \) by the period of 12, while others substituted an ordered pair such as \((4{\text{, }}10)\)and solved for B, often correctly. Many found that \(c = 17\) , thus confusing the vertical translation with a y-intercept.
For (c), many candidates simply read approximate values from the graph where \(y = 12\) and thus answered with \(t = 3.5\) and \(t = 10.5\) . Although the latter value is correct to three significant figures, \(t = 3.5\) incurs the accuracy penalty as it was expected that candidates calculate this value in their GDC to achieve a result of \(t = 3.52\) . Those who attempted an analytic approach rarely achieved correct results.

