| Date | May 2010 | Marks available | 1 | Reference code | 10M.2.sl.TZ1.5 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Write down | Question number | 5 | Adapted from | N/A |
Question
The graph of \(y = p\cos qx + r\) , for \( - 5 \le x \le 14\) , is shown below.
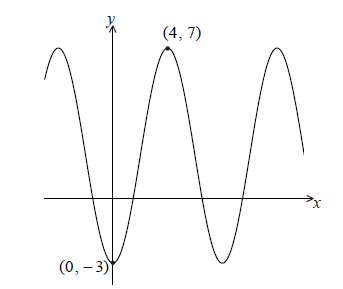
There is a minimum point at (0, −3) and a maximum point at (4, 7) .
Find the value of
(i) p ;
(ii) q ;
(iii) r.
The equation \(y = k\) has exactly two solutions. Write down the value of k.
Markscheme
(i) evidence of finding the amplitude (M1)
e.g. \(\frac{{7 + 3}}{2}\) , amplitude \(= 5\)
\(p = - 5\) A1 N2
(ii) period \(= 8\) (A1)
\(q = 0.785\) \(\left( { = \frac{{2\pi }}{8} = \frac{\pi }{4}} \right)\) A1 N2
(iii) \(r = \frac{{7 - 3}}{2}\) (A1)
\(r = 2\) A1 N2
[6 marks]
\(k = - 3\) (accept \(y = - 3\) ) A1 N1
[1 mark]
Examiners report
Many candidates did not recognize that the value of p was negative. The value of q was often interpreted incorrectly as the period but most candidates could find the value of r, the vertical translation.
In part (b), candidates either could not find a solution or found too many.

