| Date | May 2013 | Marks available | 3 | Reference code | 13M.2.sl.TZ1.10 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Find | Question number | 10 | Adapted from | N/A |
Question
A Ferris wheel with diameter \(122\) metres rotates clockwise at a constant speed. The wheel completes \(2.4\) rotations every hour. The bottom of the wheel is \(13\) metres above the ground.
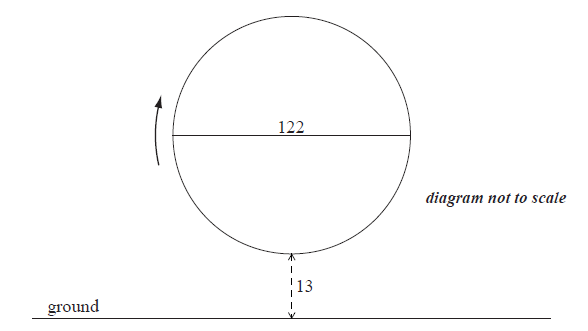
A seat starts at the bottom of the wheel.
After t minutes, the height \(h\) metres above the ground of the seat is given by\[h = 74 + a\cos bt {\rm{ .}}\]
Find the maximum height above the ground of the seat.
(i) Show that the period of \(h\) is \(25\) minutes.
(ii) Write down the exact value of \(b\) .
(b) (i) Show that the period of \(h\) is \(25\) minutes.
(ii) Write down the exact value of \(b\) .
(c) Find the value of \(a\) .
(d) Sketch the graph of \(h\) , for \(0 \le t \le 50\) .
Find the value of \(a\) .
Sketch the graph of \(h\) , for \(0 \le t \le 50\) .
In one rotation of the wheel, find the probability that a randomly selected seat is at least \(105\) metres above the ground.
Markscheme
valid approach (M1)
eg \(13 + {\rm{diameter}}\) , \(13 + 122\)
maximum height \( = 135\) (m) A1 N2
[2 marks]
(i) period \( = \frac{{60}}{{2.4}}\) A1
period \( = 25\) minutes AG N0
(ii) \(b = \frac{{2\pi }}{{25}}\) \(( = 0.08\pi )\) A1 N1
[2 marks]
(a) (i) period \( = \frac{{60}}{{2.4}}\) A1
period \( = 25\) minutes AG N0
(ii) \(b = \frac{{2\pi }}{{25}}\) \(( = 0.08\pi )\) A1 N1
[2 marks]
(b) METHOD 1
valid approach (M1)
eg \({\rm{max}} - 74\) , \(\left| a \right| = \frac{{135 - 13}}{2}\) , \(74 - 13\)
\(\left| a \right| = 61\) (accept \(a = 61\) ) (A1)
\(a = - 61\) A1 N2
METHOD 2
attempt to substitute valid point into equation for h (M1)
eg \(135 = 74 + a\cos \left( {\frac{{2\pi \times 12.5}}{{25}}} \right)\)
correct equation (A1)
eg \(135 = 74 + a\cos (\pi )\) , \(13 = 74 + a\)
\(a = - 61\) A1 N2
[3 marks]
(c)
A1A1A1A1 N4
Note: Award A1 for approximately correct domain, A1 for approximately correct range,
A1 for approximately correct sinusoidal shape with \(2\) cycles.
Only if this last A1 awarded, award A1 for max/min in approximately correct positions.
[4 marks]
Total [9 marks]
METHOD 1
valid approach (M1)
eg \({\rm{max}} - 74\) , \(\left| a \right| = \frac{{135 - 13}}{2}\) , \(74 - 13\)
\(\left| a \right| = 61\) (accept \(a = 61\) ) (A1)
\(a = - 61\) A1 N2
METHOD 2
attempt to substitute valid point into equation for h (M1)
eg \(135 = 74 + a\cos \left( {\frac{{2\pi \times 12.5}}{{25}}} \right)\)
correct equation (A1)
eg \(135 = 74 + a\cos (\pi )\) , \(13 = 74 + a\)
\(a = - 61\) A1 N2
[3 marks]
A1A1A1A1 N4
Note: Award A1 for approximately correct domain, A1 for approximately correct range,
A1 for approximately correct sinusoidal shape with \(2\) cycles.
Only if this last A1 awarded, award A1 for max/min in approximately correct positions.
[4 marks]
setting up inequality (accept equation) (M1)
eg \(h > 105\) , \(105 = 74 + a\cos bt\) , sketch of graph with line \(y = 105\)
any two correct values for t (seen anywhere) A1A1
eg \(t = 8.371 \ldots \) , \(t = 16.628 \ldots \) , \(t = 33.371 \ldots \) , \(t = 41.628 \ldots \)
valid approach M1
eg \(\frac{{16.628 - 8.371}}{{25}}\) , \(\frac{{{t_1} - {t_2}}}{{25}}\) , \(\frac{{2 \times 8.257}}{{50}}\) , \(\frac{{2(12.5 - 8.371)}}{{25}}\)
\(p = 0.330\) A1 N2
[5 marks]
Examiners report
Most candidates were successful with part (a).
A surprising number had difficulty producing enough work to show that the period was \(25\); writing down the exact value of \(b\) also overwhelmed a number of candidates. In part (c), candidates did not recognize that the seat on the Ferris wheel is a minimum at \(t = 0\) thereby making the value of a negative. Incorrect values of \(61\) were often seen with correct follow through obtained when sketching the graph in part (d). Graphs again frequently failed to show key features in approximately correct locations and candidates lost marks for incorrect domains and ranges.
A surprising number had difficulty producing enough work to show that the period was \(25\); writing down the exact value of \(b\) also overwhelmed a number of candidates. In part (c), candidates did not recognize that the seat on the Ferris wheel is a minimum at \(t = 0\) thereby making the value of a negative. Incorrect values of \(61\) were often seen with correct follow through obtained when sketching the graph in part (d). Graphs again frequently failed to show key features in approximately correct locations and candidates lost marks for incorrect domains and ranges.
A surprising number had difficulty producing enough work to show that the period was \(25\); writing down the exact value of \(b\) also overwhelmed a number of candidates. In part (c), candidates did not recognize that the seat on the Ferris wheel is a minimum at \(t = 0\) thereby making the value of a negative. Incorrect values of \(61\) were often seen with correct follow through obtained when sketching the graph in part (d). Graphs again frequently failed to show key features in approximately correct locations and candidates lost marks for incorrect domains and ranges.
A surprising number had difficulty producing enough work to show that the period was \(25\); writing down the exact value of \(b\) also overwhelmed a number of candidates. In part (c), candidates did not recognize that the seat on the Ferris wheel is a minimum at \(t = 0\) thereby making the value of a negative. Incorrect values of \(61\) were often seen with correct follow through obtained when sketching the graph in part (d). Graphs again frequently failed to show key features in approximately correct locations and candidates lost marks for incorrect domains and ranges.
Part (e) was very poorly done for those who attempted the question and most did not make the connection between height, time and probability. The idea of linking probability with a real-life scenario proved beyond most candidates. That said, there were a few novel approaches from the strongest of candidates using circles and angles to solve this part of question 10.

