| Date | November 2014 | Marks available | 2 | Reference code | 14N.2.sl.TZ0.5 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 5 | Adapted from | N/A |
Question
The following diagram shows part of the graph of \(y = p\sin (qx) + r\).
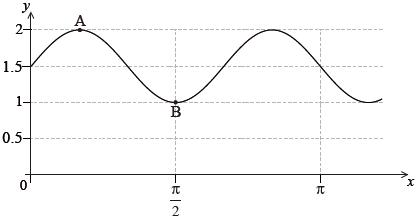
The point \({\text{A}}\left( {\frac{\pi }{6},{\text{ }}2} \right)\) is a maximum point and the point \({\text{B}}\left( {\frac{\pi }{6},{\text{ }}1} \right)\) is a minimum point.
Find the value of
\(p\);
\(r\);
\(q\).
Markscheme
valid approach (M1)
eg\(\;\;\;\)\(\frac{{2 - 1}}{2},{\text{ }}2 - 1.5\)
\(p = 0.5\) A1 N2
[2 marks]
valid approach (M1)
eg\(\;\;\;\)\(\frac{{1 + 2}}{2}\)
\(r = 1.5\) A1 N2
[2 marks]
METHOD 1
valid approach (seen anywhere) M1
eg\(\;\;\;\)\(q = \frac{{2\pi }}{{{\text{period}}}},{\text{ }}\frac{{2\pi }}{{\left( {\frac{{2\pi }}{3}} \right)}}\)
period \( = \frac{{2\pi }}{3}\)\(\;\;\;\)(seen anywhere) (A1)
\(q = 3\) A1 N2
METHOD 2
attempt to substitute one point and their values for \(p\) and \(r\) into \(y\) M1
eg\(\;\;\;\)\(2 = 0.5\sin \left( {q\frac{\pi }{6}} \right) + 1.5,{\text{ }}\frac{\pi }{2} = 0.5\sin (q1) + 1.5\)
correct equation in \(q\) (A1)
eg\(\;\;\;\)\(q\frac{\pi }{6} = \frac{\pi }{2},{\text{ }}q\frac{\pi }{2} = \frac{{3\pi }}{2}\)
\(q = 3\) A1 N2
METHOD 3
valid reasoning comparing the graph with that of \(\sin x\) R1
eg\(\;\;\;\)position of max/min, graph goes faster
correct working (A1)
eg\(\;\;\;\)max at \(\frac{\pi }{6}\) not at \(\frac{\pi }{2}\), graph goes \(3\) times as fast
\(q = 3\) A1 N2
[3 marks]
Total [7 marks]
Examiners report
Many candidates found the correct value for the amplitude and vertical shift, but very few managed to find the correct value of the period and therefore of \(q\) in part (c). Some candidates substituted the coordinates of a point into the function but were not able to write a correct equation in terms of \(q\). Many candidates who found the correct answer did not show sufficient work to gain all three marks. The rubrics stress the need to show working.
Many candidates found the correct value for the amplitude and vertical shift, but very few managed to find the correct value of the period and therefore of \(q\) in part (c). Some candidates substituted the coordinates of a point into the function but were not able to write a correct equation in terms of \(q\). Many candidates who found the correct answer did not show sufficient work to gain all three marks. The rubrics stress the need to show working.
Many candidates found the correct value for the amplitude and vertical shift, but very few managed to find the correct value of the period and therefore of \(q\) in part (c). Some candidates substituted the coordinates of a point into the function but were not able to write a correct equation in terms of \(q\). Many candidates who found the correct answer did not show sufficient work to gain all three marks. The rubrics stress the need to show working.

