| Date | May 2014 | Marks available | 2 | Reference code | 14M.2.sl.TZ2.6 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find | Question number | 6 | Adapted from | N/A |
Question
Let \(f(x) = p\cos \left( {q(x + r)} \right) + 10\), for \(0 \leqslant x \leqslant 20\). The following diagram shows the graph of \(f\).
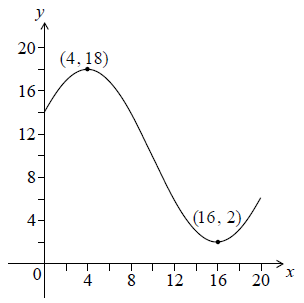
The graph has a maximum at \((4, 18)\) and a minimum at \((16, 2)\).
Write down the value of \(r\).
Find \(p\).
Find \(q\).
Solve \(f(x) = 7\).
Markscheme
\(r = - 4\) A2 N2
Note: Award A1 for \(r = 4\).
[2 marks]
evidence of valid approach (M1)
eg \(\frac{{\max y{\text{ value -- }}y{\text{ value}}}}{2}\), distance from \(y = 10\)
\(p = 8\) A1 N2
[2 marks]
valid approach (M1)
eg period is \(24\), \(\frac{{360}}{{24}}\), substitute a point into their \(f(x)\)
\(q = \frac{{2\pi }}{{24}}\left( {\frac{\pi }{{12}},{\text{ exact}}} \right)\), \(0.262\) (do not accept degrees) A1 N2
[2 marks]
valid approach (M1)
eg line on graph at \(y = 7,{\text{ }}8\cos \left( {\frac{{2\pi }}{{24}}(x - 4)} \right) + 10 = 7\)
\(x = 11.46828\)
\(x = 11.5\) (accept \((11.5, 7)\)) A1 N2
[2 marks]
Note: Do not award the final A1 if additional values are given. If an incorrect value of \(q\) leads to multiple solutions, award the final A1 only if all solutions within the domain are given.

