| Date | November 2010 | Marks available | 6 | Reference code | 10N.2.sl.TZ0.10 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 10 | Adapted from | N/A |
Question
The following diagram represents a large Ferris wheel at an amusement park.
The points P, Q and R represent different positions of a seat on the wheel.
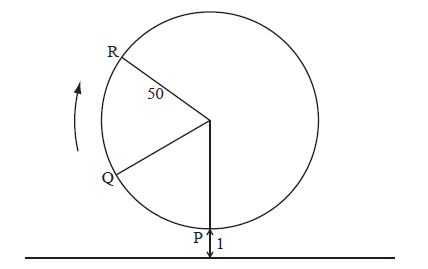
The wheel has a radius of 50 metres and rotates clockwise at a rate of one revolution every 30 minutes.
A seat starts at the lowest point P, when its height is one metre above the ground.
Find the height of a seat above the ground after 15 minutes.
After six minutes, the seat is at point Q. Find its height above the ground at Q.
The height of the seat above ground after t minutes can be modelled by the function \(h(t) = 50\sin (b(t - c)) + 51\).
Find the value of b and of c .
The height of the seat above ground after t minutes can be modelled by the function \(h(t) = 50\sin (b(t - c)) + 51\).
Hence find the value of t the first time the seat is \(96{\text{ m}}\) above the ground.
Markscheme
valid approach (M1)
e.g. 15 mins is half way, top of the wheel, \(d + 1\)
height \( = 101\) (metres) A1 N2
[2 marks]
evidence of identifying rotation angle after 6 minutes A1
e.g. \(\frac{{2\pi }}{5}\) , \(\frac{1}{5}\) of a rotation, \({72^ \circ }\)
evidence of appropriate approach (M1)
e.g. drawing a right triangle and using cosine ratio
correct working (seen anywhere) A1
e.g. \(\cos \frac{{2\pi }}{5} = \frac{x}{{50}}\) , \(15.4(508 \ldots )\)
evidence of appropriate method M1
e.g. height \(= {\rm{radius}} + 1 - 15.45 \ldots \)
height \(= 35.5\) (metres) (accept 35.6) A1 N2
[5 marks]
METHOD 1
evidence of substituting into \(b = \frac{{2\pi }}{{{\rm{period}}}}\) (M1)
correct substitution
e.g. period = 30 minutes, \(b = \frac{{2\pi }}{{30}}\) A1
\(b = 0.209\) \(\left( {\frac{\pi }{{15}}} \right)\) A1 N2
substituting into \(h(t)\) (M1)
e.g. \(h(0) = 1\) , \(h(15) = 101\)
correct substitution A1
\(1 = 50\sin \left( { - \frac{\pi }{{15}}c} \right) + 51\)
\(c = 7.5\) A1 N2
METHOD 2
evidence of setting up a system of equations (M1)
two correct equations
e.g. \(1 = 50\sin b(0 - c) + 51\) , \(101 = 50\sin b(15 - c) + 51\) A1A1
attempt to solve simultaneously (M1)
e.g. evidence of combining two equations
\(b = 0.209\) \(\left( {\frac{\pi }{{15}}} \right)\) , \(c = 7.5\) A1A1 N2N2
[6 marks]
evidence of solving \(h(t) = 96\) (M1)
e.g. equation, graph
\(t = 12.8\) (minutes) A2 N3
[3 marks]
Examiners report
Part (a) was well done with most candidates obtaining the correct answer.
Part (b) however was problematic with most errors resulting from incorrect, missing or poorly drawn diagrams. Many did not recognize this as a triangle trigonometric problem while others used the law of cosines to find the chord length rather than the vertical height, but this was only valid if they then used this to complete the problem. Many candidates misinterpreted the question as one that was testing arc length and area of a sector and made little to no progress in part (b).
Still, others recognized that 6 minutes represented \(\frac{1}{5}\) of a rotation, but the majority then thought the height after 6 minutes should be \(\frac{1}{5}\) of the maximum height, treating the situation as linear. There were even a few candidates who used information given later in the question to answer part (b). Full marks are not usually awarded for this approach.
Part (c) was not well done. It was expected that candidates simply use the formula \(\frac{{2\pi }}{{{\rm{period}}}}\) to find the value of b and then substitute back into the equation to find the value of c. However, candidates often preferred to set up a pair of equations and attempt to solve them analytically, some successful, some not. No attempts were made to solve this system on the GDC indicating that candidates do not get exposed to many “systems” that are not linear. Confusing radians and degrees here did nothing to improve the lack of success.
In part (d), candidates were clear on what was required and set their equation equal to 96. Yet again however, solving this equation graphically using a GDC proved too daunting a task for most.

